计算机存储体系：量化分析与并行存储

任何一个单一的存储器都难以同时完成容量大，速度快，价格便宜的需求，所以这个时候较好的方法是采用存储层次，用多种存储器构成存储器的层次结构。

为什么可以怎么做？有两个理由

1. 局部性原理
2. 加快经常性事件

思路是将经常使用的局部性程序和数据放到更快，更小，但更贵的存储器中

这就需要用采用量化分析来判断存储系统的好坏

存储器性能的量化

首先，如何定量衡量一个存储器的好坏？主要是容量和速度，以及价格C

1. 容量\(S\)：

存储器容量\(S_M=Wlm\)

\(w\):存储器字长

\(l\):字数

\(m\):并行工作存储体的个数

2. 速度（访问时间）

访问时间\(T_A\)：从接到访存读申请，到信息被读到数据总线上所需的时间

访存周期\(T_M\)：连续启动一个存储体所需要的间隔时间，即两次存取操作所需要的最小时间间隔

带宽\(B_m\)：存储器可提供的数据传送速率,单位时间内能传送二进制字节数

如果采用最简单的单体单字的存储器

意味着字长与CPU字长相同，每一次只能访问一个存储字，即：\(B_m = \frac{W}{T_m}\)

并行存储系统

怎样可以提高带宽呢？

如果在一个访存周期内可以并行访问多个存储字，能有效提高存储器的带宽。

单体多字存储器

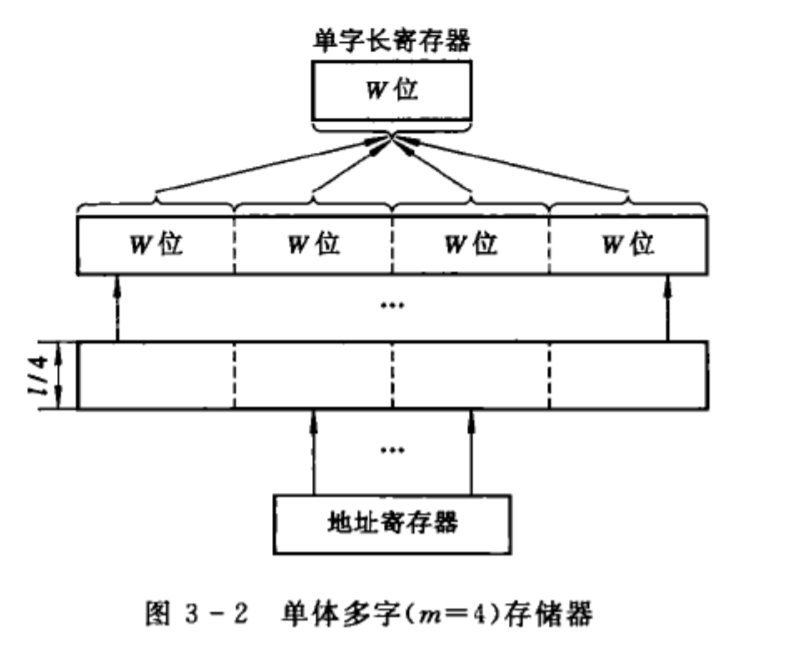
如图。一次可以取四个字，所以易得有\(B_m=W*4/T_m\)

逻辑实现：把地址码分成两个部分

一部分仍作为存储器的地址，另一部分负责从m个数据中选择一个数据

这个方法并不好，会有很多问题：

• 如果一次读取的m个指令字中有分支跳转指令，而且成功了，意味着该指令后面的指令是无用的。

• 这一次取到的m个数据不一定都是有用的，假设当前的指令需要多个操作数，也不一定正好全部一次取到。

• 假设这个存储周期存在对同一个存储单元的写和读，写入之后那读的操作就发生错误了。

多体单字存储器

由多个单体存储器构成，每个都有自己的地址寄存器以及地址译码和读/写驱动等电路

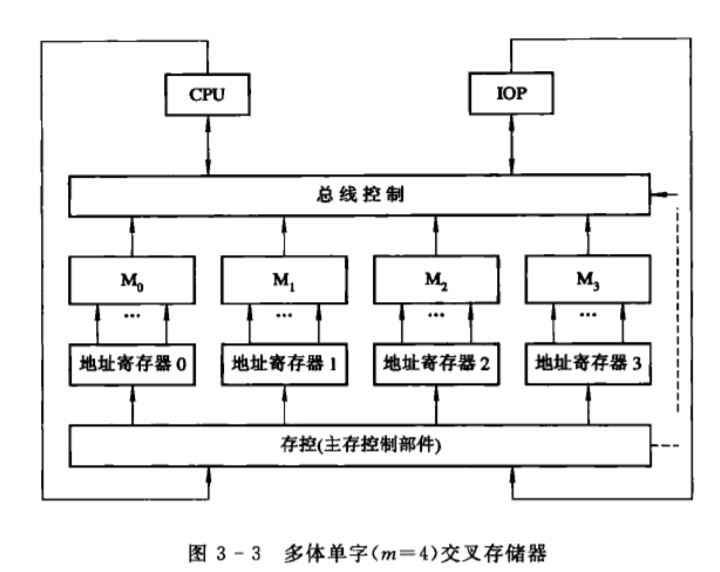
存储器的每个存储单元都要给定一个地址才能被访问到。并行存储器是由多个存储体组成，并行存取可以加快存取速度，但是这和编址方法有关。

如何编址？存储器是按顺序编址的。所以要建立一维数组与二维矩阵之间的转化

分为高位交叉和低位交叉，也叫做按列优先编址和按行优先编址

• 高位交叉编址

高位交叉编址是对存储单元按体内地址顺序存放，每个存储体内的地址是连续

这种编址方法如果每次都只访问一个存储体，对单处理机而言就没有并行的效果

• 低位交叉编址

这种编址方法是横向的，连续的地址分布在相邻的存储体中，这样对于一个存储体，地址不是连续的，对于单处理及可以并行存取。

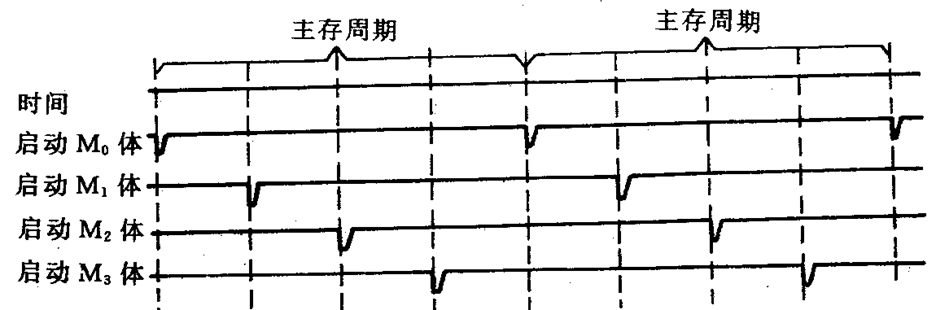
分时启动

m个存储体分时启动，实际上是一种采用流水线方式工作的并行存储器。

在每个存储周期内，分时启动m个存储体，如果每个存储体的访问周期是\(T_M\)，则时间间隔是\(t=\frac{T_M}{m}\)

那么是不是\(m\)越多越好，并不是。

原因：
1)模m越高，存贮器数据总线越长，导致传输延迟增加；
2)系统效率问题，对于顺序取指，效率可以提高m倍，但遇到转移指令，效率就会下降。

存储系统的量化分析

上文总结了单一存储器的量化分析，现在来分析一下对于整个存储系统，如何量化判断？

多级层次结构

首先简单了解一下存储系统的多级层次结构

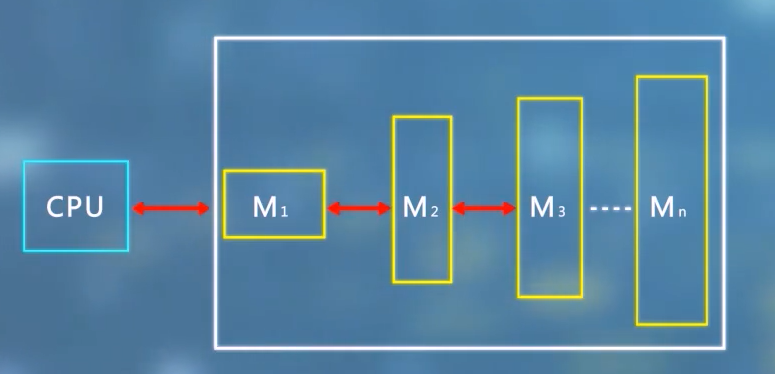
容量：

\(S_1<S_2<S_3<S_n\)

速度:

\(M_1>M_2>M_3>M_4\)

这个存储系统要达到的目标，从CPU看，存储系统的速度接近于\(M_1\)，而容量接近于\(M_n\)。

大部分的访问要尽量在\(M_1\)完成

存储系统的性能参数

为了简化分析，我们从两级存储系统进行考虑

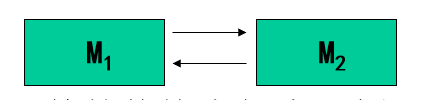
• 每位价格\(C\)

\(C=\frac{C_1S_1+C_2S_2}{S_1+S_2}\)

当\(S_1<<S_2\),\(C\)约等于\(C_2\)

• 命中率\(H\)与不命中率\(F\)

命中率就CPU访问存储系统时，在\(M_1\)中找到所需信息的概率

\(N_1\)代表在\(M_1\)找到信息的次数

\(H=\frac{N_1}{N_1+N_2}\)

\(F=1-H\)

• 等效访问时间

可以分两种情况考虑：

• 命中\(T_1\)：访问时间为\(T_1\)，命中的概率为\(H\)
• 不命中\(T_M\)：从\(M_2\)发出访问请求到整个数据块装入\(M_1\)所需要的时间：\(T_2+T_B\)

\(T_B\)是传送一个信息块的时间。

还需要再加上\(T_1\)

所以等效访问时间：

\[T_A = HT1+(1-H)(T_1+T_M)=T_1+(1-H)T_M \]

\[T_A = T_1+FT_M \]

根据等效时间得出访问效率：

\[e=\frac{T_1}{T_A}=\frac{HT_1}{HT_1+(1-H)T_M}=\frac{1}{H+(1-H)r} \]

\(r\)是指相邻两级的访问时间比\(\frac{T1}{T_2}\),不考虑传送时间的情况下。

这个式子证明若要提高访问效率，要提高命中率\(H\)，但是命中率\(H\)与程序和其他方面有关，比较难提高，通过系统结构解决的方法是降低访问时间比\(r\)

通过下面的方法来实现：

• 减小相邻两级的访问速度差距

• 减小相邻两级存贮器的容量差

这也证明了cache与主存访问速度不能差距太大

来源

[1] 计算机系统结构课本

[2] 计算机系统结构 华中科技大学 中国大学MOOC