顺时针打印矩阵

题目

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]

输出：[1,2,3,6,9,8,7,4,5]

解题思路

考虑设定矩阵的“左、上、右、下”四个边界，模拟以上矩阵遍历顺序

 

 

 

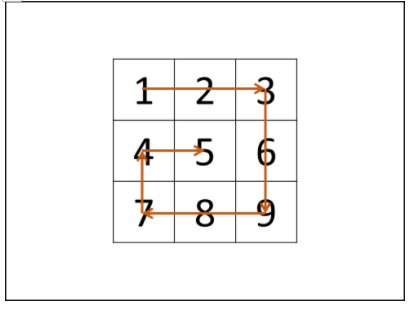
算法流程：　　

　　空值处理： 当 matrix 为空时，直接返回空列表 [] 即可。
　　1.初始化： 矩阵 左、右、上、下 四个边界 l , r , t , b ，用于打印的结果列表 res 。
　　2.循环打印： “从左向右、从上向下、从右向左、从下向上” 四个方向循环，每个方向打印中做以下三件事 （各方向的具体信息见下表） ；
　　3.根据边界打印，即将元素按顺序添加至列表 res 尾部；
　　　　边界向内收缩 11 （代表已被打印）；
　　　　判断是否打印完毕（边界是否相遇），若打印完毕则跳出。
　　4.返回值： 返回 res 即可。

• 打印方向  1. 根据边界打印  2. 边界向内收缩  3. 是否打印完毕
• 从左向右 左边界l ，右边界 r 上边界 t 加 11  是否 t > b
• 从上向下 上边界 t ，下边界b 右边界 r 减 11 是否 l > r
• 从右向左 右边界 r ，左边界l 下边界 b 减 11 是否 t > b
• 从下向上 下边界 b ，上边界t 左边界 l 加 11 是否 l > r

复杂度分析：

时间复杂度 O(MN)O(MN) ： M, NM,N 分别为矩阵行数和列数。
空间复杂度 O(1)O(1) ： 四个边界 l , r , t , b 使用常数大小的 额外 空间（ res 为必须使用的空

代码

func spiralOrder(matrix [][]int) []int {
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return []int{}
    }
    rows, columns := len(matrix), len(matrix[0])
    visited := make([][]bool, rows)
    for i := 0; i < rows; i++ {
        visited[i] = make([]bool, columns)
    }

    var (
        total = rows * columns
        order = make([]int, total)
        row, column = 0, 0
        directions = [][]int{[]int{0, 1}, []int{1, 0}, []int{0, -1}, []int{-1, 0}}
        directionIndex = 0
    )

    for i := 0; i < total; i++ {
        order[i] = matrix[row][column]
        visited[row][column] = true
        nextRow, nextColumn := row + directions[directionIndex][0], column + directions[directionIndex][1]
        if nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn] {
            directionIndex = (directionIndex + 1) % 4
        }
        row += directions[directionIndex][0]
        column += directions[directionIndex][1]
    }
    return order
}