状压DP详解（位运算）

前言：

状压DP是一种非常暴力的做法（有一些可以排除某些状态的除外），例如dp[S][v]中，S可以代表已经访问过的顶点的集合，v可以代表当前所在的顶点为v。S代表的就是一种状态（二进制表示），比如  (11001)₂  代表在二进制中{0，3，4}三个顶点已经访问过了，(11001)₂ 代表的十进制数就是25 ，所以当S为25的时候其实就是代表已经访问过了{0，3，4}三个顶点，那假如一共有5个顶点（标号为01234）的话，所有的顶点都访问完毕应该S为什么呢？是　(11111)_2。

那么，在状态转移的过程中我们势必要对十进制数转化为二进制数的每一个的位数进行一些操作。下面，列举了一些位运算的操作。

 

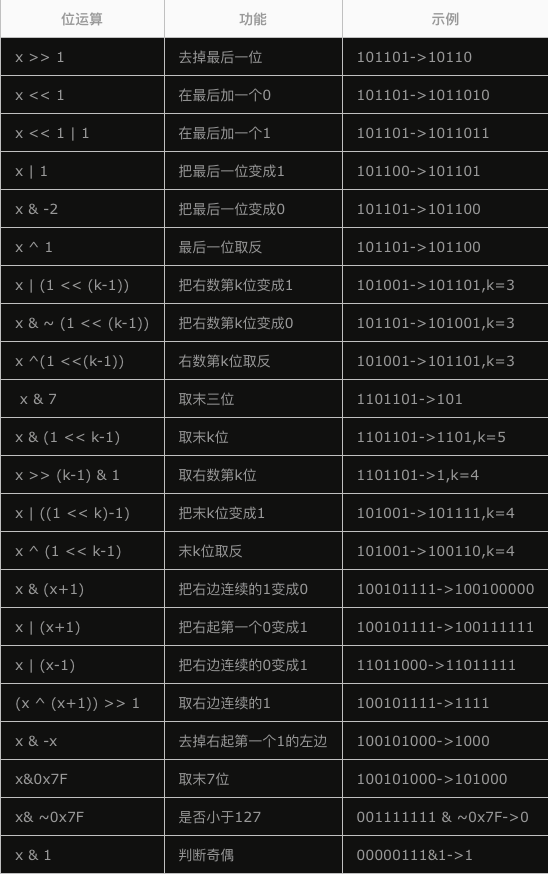
对于上面的一些操作举例一些

就如之上的　(11001)₂来说是已经访问了0，3，4三个顶点，当我接下去要访问顶点2的话可以有以下操作：1.看看第3位是什么？那么选择取出二进制数x的第k位，y = x >>(k-1) & 1，y = (110)₂ & 1 = 0，2.把第3位变为1，y = x | (1<<(k-1))，y = (11001)₂  |  (100)₂ = (11101)₂，所以顶点2访问完毕，加入到集合S中也结束了，此时S为(11101)₂ = 29。

接下去就可以开始讲一些例题了。最经典的就是白皮书上的tsp问题。

tsp问题

题意：假设有一个旅行商人要拜访N个城市，他必须选择所要走的路径，路径的限制是每个城市 只能拜访一次，而且最后要回到原来出发的城市，要求路径的总和最小。其中，2<=N<=15

思路：首先我们试着去设计状态，假设现在已经访问过的顶点的集合为S，当前所在顶点为v， 用dp[S][v]表示从v出发还有访问剩余的所有顶点，最终返回到顶点0的路径总和最小值。从v出发可以到任意一个还未访问过的顶点，边界就是访问完所有顶点并且返回到顶点0。

递推式为 
dp[V][0] = 0;(边界) 
dp[S][v] = min{dp[S∪{u}][u] + d[u][v] | u不属于S}

先通过记忆化搜索来看一下code

//  s: 已经访问过的节点状态  v: 出发位置
int dfs(int s, int v)
{
    if(dp[s][v]>=0)
        return dp[s][v];
    if(s==(1<<n)-1 && v==0)   //已经访问过所有的节点并且再次回到了0起点
        return dp[s][v]=0;
    int ans=INF;
    for(int u=0;u<n;u++)
        if(!(s>>(u &1))) // 如果u这位是0（代表没有走过的话）就走u这个节点
            ans=min(ans, dfs(s | (1<<u), u)+mp[v][u]); //dfs中第一个参数表示第u位变成1后的二进制数
    return dp[s][v]=ans;　　
}
int main()
{
    memset(dp, -1, sizeof(dp));
    printf("%d\n", dfs(0, 0));
    return 0;
}

 

 但是在这个问题中，对于任意两个整数i和j，如果他们对应的集合满足S（i）包含于S（j），就有i<=j，因此我们可以写成循环的方式。

int dp[1<<maxn][maxn];

void solve()
{
    for(int S = 0; S < 1<<n; S++)
    {
        fill(dp[S],dp[S]+n,INF);  //初始化
    }
    dp[(1<<n) - 1][0] = 0; //边界条件
    //之前的记忆化搜索转换为递推式
    for(int S = (1<<n) - 2; S >= 0; S--)
    {
        for(int v = 0; v < n; v++)
        {
            for(int u = 0; u < n; u++)
            {
                if(!(S>>u&1)){ //如果u不属于S集合
                    dp[S][v] = min(dp[S][v],dp[S|1<<u][u]+d[v][u]);
                }
            }
        }
    }
    printf("%d\n",dp[0][0]);
}

这样子，一个状压DP的板子差不多就出来了。