机器学习聚类算法之K-means

一、概念

K-means是一种典型的聚类算法，它是基于距离的，是一种无监督的机器学习算法。

K-means需要提前设置聚类数量，我们称之为簇，还要为之设置初始质心。

缺点：

1、循环计算点到质心的距离，复杂度较高。

2、对噪声不敏感，即使是噪声也会被聚类。

3、质心数量及初始位置的选定对结果有一定的影响。

 

二、计算

K-means需要循环的计算点到质心的距离，有三种常用的方法：

1、欧式距离

欧式距离源自N维欧氏空间中两点x，y间的距离公式，在二维上（x1，y1）到（x2，y2）的距离体现为：

在三维上体现为：

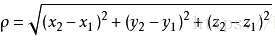
欧式距离是K-means最常用的计算距离的方法。

 

2、曼哈顿距离

在二维上（x1，y1）到（x2，y2）的距离体现为：

 

3、余弦夹角

余弦距离不是距离，而只是相似性，其他距离直接测量两个高维空间上的点的距离，如果距离为0则两个点“相同”；
余弦的结果为在[-1，1]之中，如果为 1，只能确定两者完全相关、完全相似。

在二维上（x1，y1）到（x2，y2）的距离体现为：

 

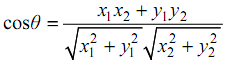
 聚类的基本步骤：

1、设置质心个数，这代表最终聚类数；

2、根据质心个数随机生成初始质心点；

3、计算数据与质心距离，根据距离远近做第一次分类；

4、将聚类结果的中心点定义为新的质心，再进行3的计算；

5、循环迭代直到质心不再变化，此为最终结果。

 

3、实现

 

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt


def create_sample():
    np.random.seed(10)  # 随机数种子，保证随机数生成的顺序一样
    n_dim = 2
    num = 100
    a = 3 + 5 * np.random.randn(num, n_dim)
    b = 18 + 4 * np.random.randn(num, n_dim)
    data_mat = np.concatenate((a, b))
    ay = np.zeros(num)
    by = np.ones(num)
    label = np.concatenate((ay, by))
    return {'data_mat': data_mat, 'label': label}


# arr[i, :] #取第i行数据
# arr[i:j, :] #取第i行到第j行的数据
# in:arr[:,0] # 取第0列的数据，以行的形式返回的
# in:arr[:,:1] # 取第0列的数据，以列的形式返回的

def k_mean(data_set, k):
    m, n = np.shape(data_set)  # 获取维度, 行数，列数
    cluster_assignment = np.mat(np.zeros((m, 2)))  # 转换为矩阵， zeros生成指定维数的全0数组，用来记录迭代结果
    centroids = generate_centroids(k, n)
    cluster_changed = True
    while cluster_changed:
        cluster_changed = False
        for i in range(m):
            min_distance = np.inf  # 无限大的正数
            min_index = -1
            vec_b = np.array(data_set)[i, :]  # i行数据，数据集内的点的位置
            for j in range(k):
                vec_a = np.array(centroids)[j, :]  # j行数据， 中心点位置
                distance = calculate_distance(vec_a, vec_b)
                if distance < min_distance:
                    min_distance = distance
                    min_index = j
            if cluster_assignment[i, 0] != min_index:
                cluster_changed = True
            cluster_assignment[i, :] = min_index, min_distance ** 2
        update_centroids(data_set, cluster_assignment, centroids, k)
    get_result(data_set, cluster_assignment, k)


def generate_centroids(centroid_num, column_num):
    centroids = np.mat(np.zeros((centroid_num, column_num)))  # 生成中心点矩阵
    for index in range(centroid_num):
        # 随机生成中心点， np.random.rand（Random values in a given shape）
        centroids[index, :] = np.mat(np.random.rand(1, column_num))
    return centroids


def calculate_distance(vec_a, vec_b):
    distance = np.sqrt(sum(np.power(vec_a - vec_b, 2)))  # power(x1, x2) 对x1中的每个元素求x2次方。不会改变x1上午shape。
    return distance


def update_centroids(data_set, cluster_assignment, centroids, k):
    for cent in range(k):
        # 取出对应簇
        cluster = np.array(cluster_assignment)[:, 0] == cent
        # np.nonzero取出矩阵中非0的元素坐标
        pts_in_cluster = data_set[np.nonzero(cluster)]
        # print(pts_in_cluster)
        # mean() 函数功能：求取均值
        # 经常操作的参数为axis，以m * n矩阵举例：
        # axis : 不设置值,  m * n 个数求均值，返回一个实数
        # axis = 0：压缩行，对各列求均值，返回1 * n矩阵
        # axis = 1 ：压缩列，对各行求均值，返回m * 1矩阵
        if len(pts_in_cluster) > 0:
            centroids[cent, :] = np.mean(pts_in_cluster, axis=0)


def get_result(data_set, cluster_assignment, k):
    cs = ['r', 'g', 'b']
    for cent in range(k):
        ret_id = np.nonzero(np.array(cluster_assignment)[:, 0] == cent)
        plot_data(data_set[ret_id], cs[cent])
    plt.show()


def plot_data(samples, color, plot_type='o'):
    plt.plot(samples[:, 0], samples[:, 1], plot_type, markerfacecolor=color, markersize=14)


data = create_sample()
k_mean(data['data_mat'], 2)

 

聚类结果：