机器学习分类算法之随机森林

一、概念

随机森林（Random Forest）是一种由多个决策树组成的分类器，是一种监督学习算法，大部分时候是用bagging方法训练的。

bagging(bootstrap aggregating)，训练多轮，每轮的样本由原始样本中随机可放回取出n个样本组成，最终的预测函数对分类问题采用投票方式。

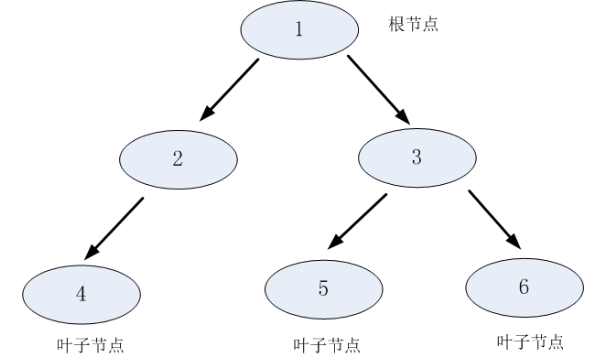
决策树利用如上图所示的树结构进行决策，每一个非叶子节点是一个判断条件，每一个叶子节点是结论。从跟节点开始，经过多次判断得出结论，每一个决策树都是一个弱分类器。

决策树每次会选择一个属性进行判断，如果不能得出结论，继续选择其他属性进行判断，直到能够“肯定地”判断出用户的类型或者是属性都已经使用完毕。

核心思想就是在一个数据集中找到一个最优特征，然后通过最优特征约束循环寻找最优特征，直到满足指定条件为止。

最优特征一般是通过信息增益或信息增益率来确定，给定一批数据集，我们可以很容易得到它的不确定性(熵)，经过一个特征的约束，数据的不确定性会降低。用两次不确定性值作差，代表不确定性降低量，降低的越多特征越好。

当数据的分类效果足够好了，比如当某个子节点内样本数目小于某一个指定值或树的最大深度达到某一个值，就可以停止了。

由上面介绍知：

bagging + 决策树 = 随机森林

比较典型的决策树有：ID3、C4.5、CART等

有两个点需要注意：

1、每个决策树的特征是有放回抽样选取的；

2、每棵树的训练数据是有返回抽样选取的；

 

二、计算

随机森林则可以通过创建随机的特征子集并使用这些子集构建较小的决策树，随后组成子树，这种方法可以防止大部分情况的过拟合，下面介绍几种典型决策树。

ID3：

算法的核心思想就是用信息增益来选择最优分类特征。

第一步：

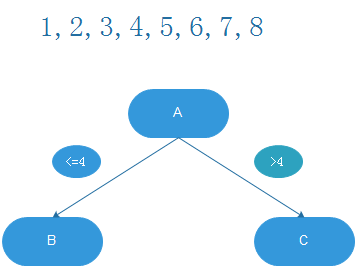
进行数据分割，分别对单个特征进行分裂，如果数据是连续的需要对数据进行离散化，如排序等距截取等，比如一组特征是1-8，就可以分为两组，见下；

第二步：

选择最优分裂属性，分别计算每一个属性的信息增益，选择信息增益最大的属性进行分裂，即该属性是分裂完后子节点的纯度最高的属性(熵比较小)。

信息增益的计算公式如下：

                                             

      其中， 表示父节点的熵； 表示节点i的熵，熵越大，节点的信息量越多，越不纯； 表示子节点i的数据量与父节点数据量之比。 越大，表示分裂后的熵越小，子节点变得越纯，分类的效果越好，因此选择 最大的属性作为分裂属性。

第三步：

停止分裂条件:

1、最小节点数
    当节点的数据量小于一个指定的数量时，不继续分裂。两个原因：一是数据量较少时，再做分裂容易强化噪声数据的作用；二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
2、熵或者基尼值小于阀值。
    熵和基尼值的大小表示数据的复杂程度，当熵或者基尼值过小时，表示数据的纯度比较大，如果熵或者基尼值小于一定程度时，节点停止分裂。
3、决策树的深度达到指定的条件
    节点的深度可以理解为节点与决策树跟节点的距离，如根节点的子节点的深度为1，因为这些节点与跟节点的距离为1，子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度，当深度到达指定的上限大小时，停止分裂。
4、所有特征已经使用完毕，不能继续进行分裂。
    被动式停止分裂的条件，当已经没有可分的属性时，直接将当前节点设置为叶子节点。

缺点：

1、特征纯度比较高(熵比较小)，该特征的子类别很多，信息增益偏向于去那些拥有很多子类的特征，不够准确。

2、不能对连续数据进行处理，需借助连续数据离散化。

 

C4.5：

第一步：

进行数据分割，分别对单个特征进行分裂，C4.5处理离散型属性的方式与ID3一致，新增对连续型属性的处理。

处理方式是先根据连续型属性进行排序，然后采用一刀切的方式将数据砍成两半，C4.5会计算每一个切割点切割后的信息增益，然后选择使分裂效果最优的切割点。

为了选取最优的切割点，要计算按每一次切割的信息增益，计算量是比较大的，可以通过去除前后两个类标签相同的切割点以简化计算的复杂度。

比如按某特征分割时，排序后连续的特征数值a，b对应的目标值是一致的，那个这两个样本之间不需要切割。

第二步：

选择最优分裂属性，C4.5采用信息增益率作为分裂的依据，

信息增益率的计算公式为：

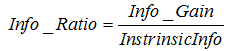
      其中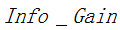表示信息增益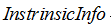，表示分裂子节点数据量的信息增益，计算公式为：

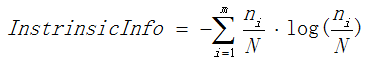
其中m表示节点的数量，Ni表示第i个节点的数据量，N表示父亲节点的数据量，说白了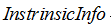，其实是分裂节点的熵。

信息增益率越大，说明分裂的效果越好。

 

CART（CART有分类树和回归树，这里先讨论分类场景）：

第一步：

进行数据分割，节点的分裂分为两种情况，连续型的数据和离散型的数据。

CART对连续型属性的处理与C4.5差不多，通过最小化分裂后的GINI值或者样本方差寻找最优分割点，将节点一分为二。

 对于离散型属性，CART是一棵二叉树，每一次分裂只会产生两个节点，需要将其中一个特征值作为一个节点，其他特征值作为另外一个节点。

例如：如果某样本一个特征有三种特征值X，Y，Z，则分裂方法有{X}、{Y，Z}；{Y}、{X，Z}；{Z}、{X，Y}，分别计算每种分裂方法的基尼值确定最优的方法。

第二步：

选择最优分裂属性，CART采用GINI值作为分裂的依据，

分裂的目的是为了能够让数据变纯，使决策树输出的结果更接近真实值。CART采用GINI值衡量节点纯度，节点越不纯，分类效果越差。

假设有k个类，样本点属于第i类的概率为pk，则GINI值的计算公式：

 

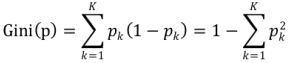
 如果样本集合D根据某个特征A被分割为D1，D2两个部分，那么在特征A的条件下，集合D的gini指数的定义为：

 

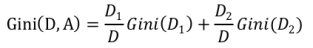
gini指数Gini(D,A)表示特征A不同分组的数据集D的不确定性。

GINI指数值越大，样本集合的不确定性也就越大。

 

三、实现

利用Python模块scikit-learn来实现随机森林。

from sklearn.ensemble import RandomForestRegressor
import numpy as np
from sklearn.datasets import load_iris

iris = load_iris()
rf = RandomForestRegressor()
rf.fit(iris.data[:], iris.target[:]) # Build a forest of trees from the training set (X, y)
instance = np.array(iris.data[-1]).reshape(1, -1) # Gives a new shape to an array without changing its data
print(iris.target[-1])
print(rf.predict(instance))