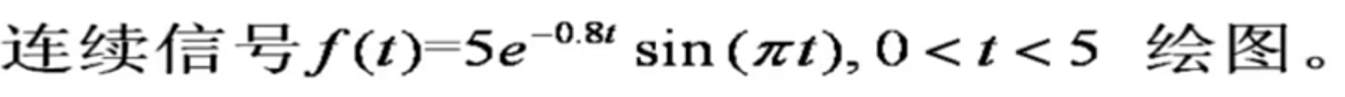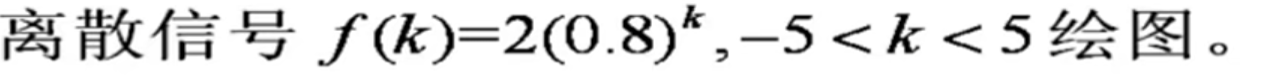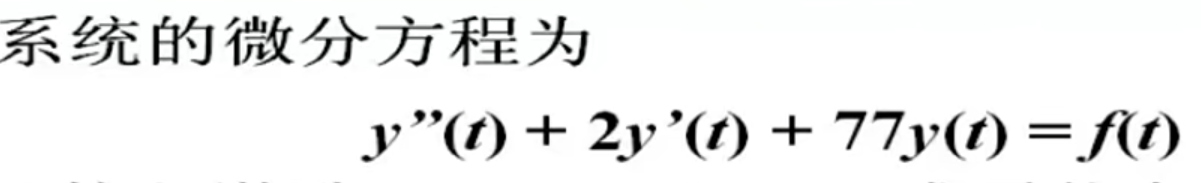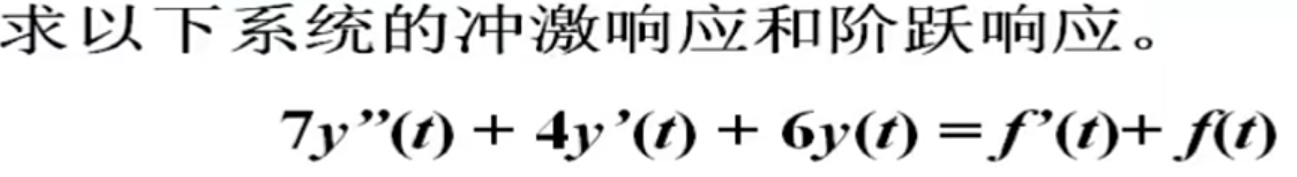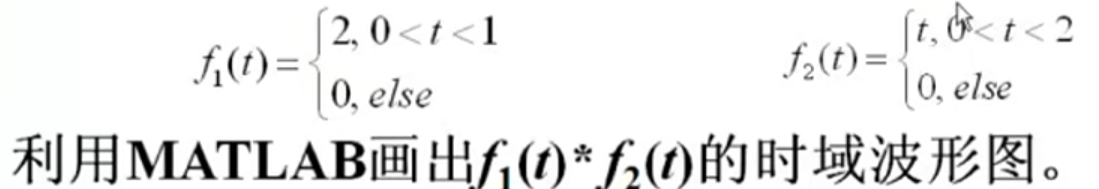1.连续信号的绘制
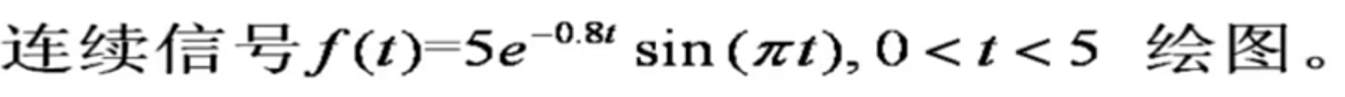
% 连续信号绘制
b = 5;
a = 0.8;
t = 0:0.001:5;
x = b*exp(-a*t.*sin(pi*t));
plot(t,x);

2.离散信号绘制
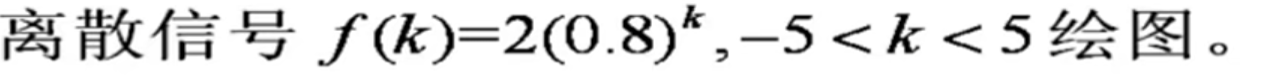
% 离散信号绘图
c = 2;
d = 0.8;
k = -5:5;
y = c*d.^k;
stem(k,y);

3.求解系统响应
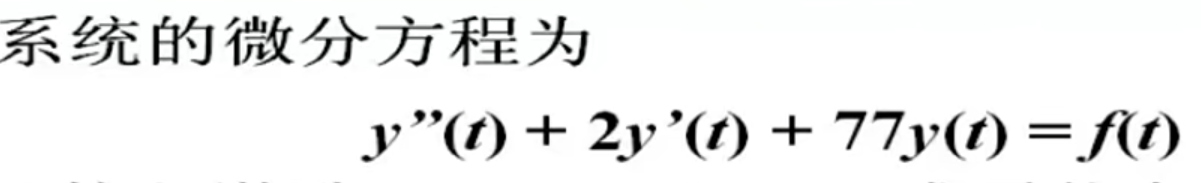
% MATLAB 求解系统响应
sys = tf([1],[1 2 77]); % tf函数获得系统模型sys
t = 0:0.01:5; % 对时间t进行离散抽样
f = 10*sin(2*pi*t);
y = lsim(sys,f,t); % 求系统的零状态响应
plot(t,y); % 画图
xlabel('Time(sec)');
ylabel('y(t)'); % 设置横纵坐标标签

4.求解系统冲激响应和阶跃响应
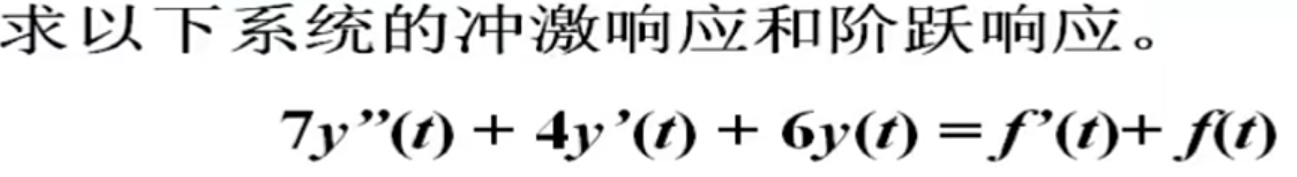
% MATLAB 求解系统冲激响应和阶跃响应
a = [7 4 6]; % 构造系数向量
b = [1 1];
subplot(2,1,1);
impulse(b,a); % 求系统冲激响应并作图
subplot(2,1,2);
step(b,a); % 求系统阶跃响应并作图

5.求解卷积运算
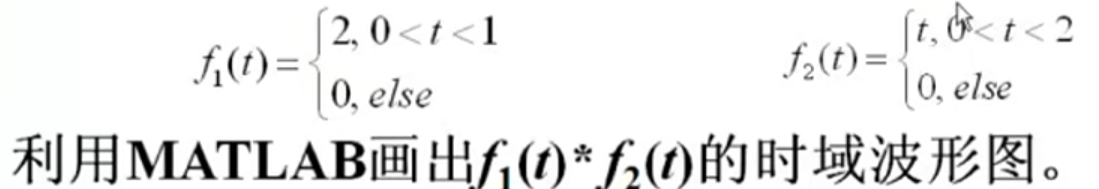
% 卷积的 MATLAB 求解
t11 = 0;t12 = 1;t21 = 0;t22 = 2;
t1 = t11:0.001:t12;
ft1 = 2*rectpuls(t1-0.5,1);
t2 = t21:0.001:t22;
ft2 = t2;
t3 = t11+t21:0.001:t12+t22; % 幅值为1,宽度为1,t1 = 0.5 点对称的方波信号
ft3 = conv(ft1,ft2);
ft3 = ft3*0.001;
plot(t3,ft3);
title('ft1(t)*ft2(t)');