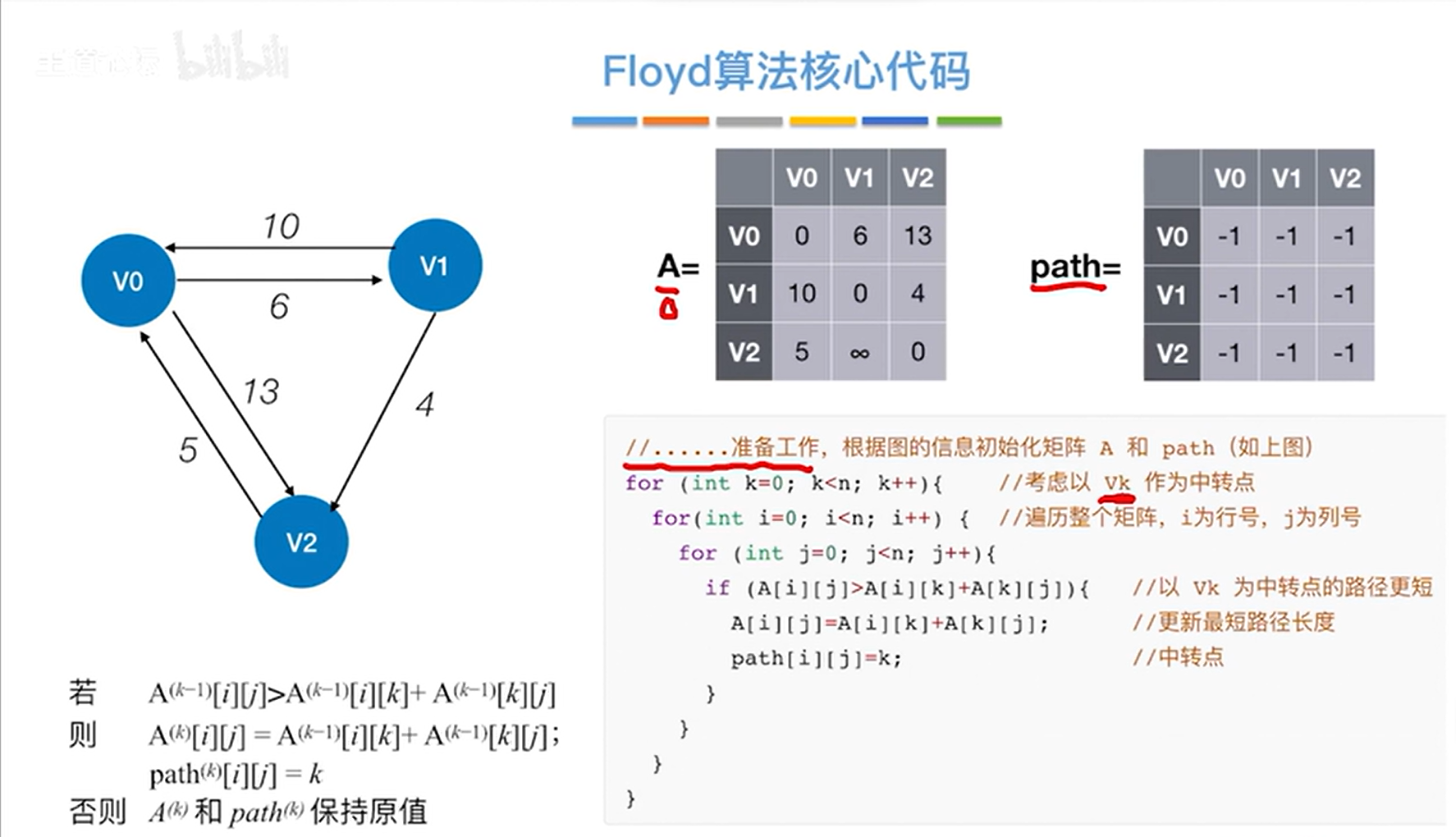
7-16 最短路径算法(Floyd-Warshall)
在带权有向图G中，求G中的任意一对顶点间的最短路径问题，也是十分常见的一种问题。
解决这个问题的一个方法是执行n次迪杰斯特拉算法，这样就可以求出每一对顶点间的最短路径，执行的时间复杂度为。
而另一种算法是由弗洛伊德提出的，时间复杂度同样是，但算法的形式简单很多。
在本题中，读入一个有向图的带权邻接矩阵（即数组表示），建立有向图并使用Floyd算法求出每一对顶点间的最短路径长度。
输入格式:
输入的第一行包含1个正整数n，表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数。对于第i行的第j个整数，如果大于0，则表示第i个顶点有指向第j个顶点的有向边，且权值为对应的整数值；如果这个整数为0，则表示没有i指向j的有向边。
当i和j相等的时候，保证对应的整数为0。
输出格式:
共有n行，每行有n个整数，表示源点至每一个顶点的最短路径长度。
如果不存在从源点至相应顶点的路径，输出-1。对于某个顶点到其本身的最短路径长度，输出0。
请在每个整数后输出一个空格，并请注意行尾输出换行。
输入样例:
4
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0输出样例:
0 3 2 1
6 0 4 7
2 5 0 3
3 6 1 0 /*
这个代码相比于原理更加简化了一些，原理中使用了俩个矩阵，
一个用来存两个点之间最短的路径长度（a），另一个用来存一个点到另一个点之间的中转点（path）
*/
#include<iostream>
using namespace std;
const int INF = 0x3f3f3f3f;
int n;
int a[51][51];
void Floyd() {
for (int k = 1; k <= n; k++) { //k是中转点
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][k] < INF && a[k][j] < INF) {
a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
//path[i][j]=k;
}
}
}
}
}
int main() {
cin >> n;
memset(a, INF, sizeof(a));
for (int i = 1; i <= n; i++) {
a[i][i] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
int x; cin >> x;
if (x != 0 || i == j) {
a[i][j] = x;
}
}
}
Floyd();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][j] == INF) cout << -1 << " ";
else cout << a[i][j] << " ";
}
cout << endl;
}
}
