树状数组入门讲解
树状数组长啥样
const int N = 1e3 + 10;
int n; // 数组范围
int data[N]; // 原始数据
int tree[N]; // 树状数组本体
inline int lowbit(int x) { return x & (-x); }
void modify(int pos, int x) { // 在 pos 处加上 x
while (pos <= n) {
tr[pos] += x;
pos += lowbit(pos);
}
}
int qry(int pos) { // 查询区间 [1, pos] 的和
int res = 0;
while (pos) {
res += tr[pos];
pos -= lowbit(pos);
}
return res;
}
lowbit
开始讲解树状数组前我们先了解一个前置知识 lowbit,它是树状数组的核心。
lowbit 是一个函数,作用是取出一个整数 x 二进制表示下最低位的 1 所代表的值。
如下面的例子:
后缀有 b 为二进制表示
12 = 1100b
lowbit(12) = 100b = 4
lowbit 实现
在 C 语言中将一个数 x 取负,等价于将 x 的二进制表示上每一位取反,再加上 1。
也就是说 -x = (~x) + 1。
signed char x = 20; (十进制)
= 00010100 (二进制)
~x = 11101011 (二进制)
-x = (~x) + 1 = 11101100 (二进制)
x & (-x) = 100 (二进制)
= 4 (十进制)
将全部二进制位取反后我们发现 x 的二进制表示下第一个 1 变成了 0,而它前面的数都变成了 1。
加上 1 对取反后的 x 而言,进位会在最低位的 0 停止,0 变成 1,它前面的低位也变回 0。
我们会发现经过取反再加 1 的操作会让 x 二进制表示下第一个 1 及其低位的位置保持不变,其他的位都是与原来相反的。这时候只需要进行与操作 & 就能取得 x 的 lowbit 了。
因此 x & (-x) 可以作为 lowbit 的一种实现。
int lowbit(int x) {
return x & (-x);
}
当然还有一种实现,可以自己研究下。
int lowbit(int x) {
return x & (x ^ (x - 1));
}
树状数组
让我们开始正式讲解树状数组,前面花了一点时间讲解 lowbit 操作,那么这个操作与树状数组有什么关系呢?
-
树状数组定义
const int N = 1e3 + 10; int data[N]; int tree[N]; // 本体tree[i]存的就是data数组中区间[i - lowbit(i) + 1, i]的和。也就是包括自己在内往前的lowbit(i)个数的和。
(这是我认为 最核心 的定义,如果在后续学习中有不理解的地方请仔细体会这句话)lowbit(20) = 4 tree[20] = data[17] + ... + data[20]; -
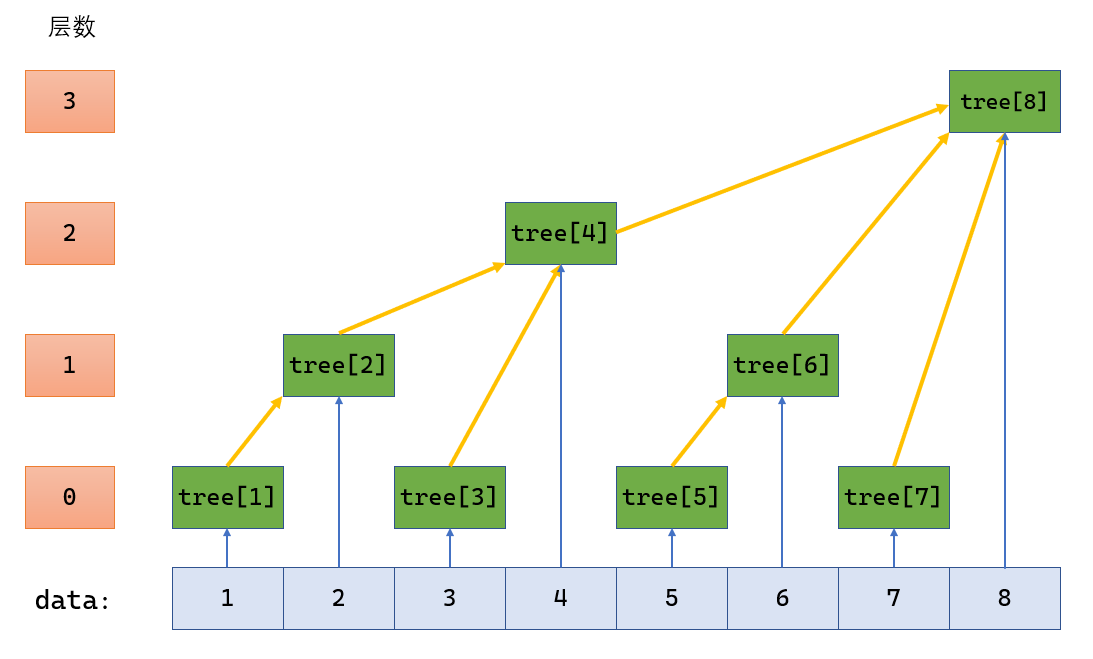
树状数组结构
![image]()
这张图怎么去理解呢?
-
黄色线代表树状数组各节点之间的更新。
-
蓝色线则代表原始数组对树状数组的更新(一般只是初始化)。
-
再进一步地,我们可以直观地看到,对于任意一个节点
tree[i]来说,它后面能将它的管理范围包括在内的最小节点就是tree[i + lowbit(i)],也就是图中的黄色箭头,表示该节点加上自身的lowbit能跳到的地方即为最小的能管理到它的节点。-
1 + lowbit(1) = 2;而
tree[2]管理的区间为[1, 2]包括了tree[1](tree[1]管理[1, 1]) -
6 + lowbit(6) = 8;而
tree[8]管理的区间为[5, 8]包括了tree[6](tree[6]管理[5, 6])
这对于树状数组的修改操作(
modify)是极为有用的。 -
-
然后,对于任意一个节点
tree[i]沿着连向它的最上边黄色线一直走就可以走到它管理的区域的最左端,也就是i - lowbit(i) + 1这个位置。而这与树状数组的查询操作(query)有关。 -
处在层数
i的节点代表这个节点管理的是大小为 \(2^i\) 的区间,\(2^i\) =lowbit(i)。
-
树状数组基础方法实现
-
我们先来看
query操作:int query(int pos) { // 查询区间 [1, pos] 的和 int res = 0; while (pos) { res += tree[pos]; pos -= lowbit(pos); } return res; }查询很好理解。当我们加上
tree[pos]后,实际上就获得了区间[pos - lowbit(pos) + 1, pos]的和了。然后将
pos减去lowbit(pos),我们就跳到了tree[pos - lowbit(pos)]这,刚好就是上一个区间的左端点前一个位置。接下来就是不断重复这一过程,直到pos变为0为止。查询的复杂度:
pos的二进制表示中最多只有31个1,每次减去lowbit后都会减少一个1,因此最多31次就会跳出循环。所以单次查询时间复杂度为 O(log n)。 -
接下来是
modify操作:int n; // 数组范围 // .... void modify(int pos, int x) { // 在 pos 处加上 x while (pos <= n) { tree[pos] += x; pos += lowbit(pos); } }当我们给
tree[pos]加上x之后,我们还要让后面的节点满足定义,也就是让所有能管理到pos这个位置的节点都加上x。而上面我们已经分析过,
pos后面 能管理到pos的最近的节点就是pos + lowbit(pos),因此我们只需要跳该位置把x加上,之后不断重复这一过程,直到pos大于n退出就好了。考虑
pos为1时的情况,每次加lowbit(pos)等价于pos * 2,而这同样最多循环31次就会跳出循环。所以单次修改复杂度为 O(log n) 。
至此,树状数组的基础部分就介绍完毕了。我们还可以将树状数组封装一下。
template <class T> struct fenwick {
int n;
std::vector<T> tr;
fenwick(int siz) : n(siz), tr(std::vector<T>(n)) {}
T &operator[](int x) { return tr[x]; }
inline int lowbit(int x) { return x & (-x); }
void add(int pos, int x) {
while (pos <= n) {
tr[pos] += x;
pos += lowbit(pos);
}
}
T qry(int pos) {
T res{};
while (pos) {
res += tr[pos];
pos -= lowbit(pos);
}
return res;
}
};
树状数组应用
- 树状数组模板1,单点修改,区间查询。
int main() {
int n, m;
std::cin >> n >> m;
fenwick<ll> t(n + 1);
for (int i = 1; i <= n; i++) {
int x;
std::cin >> x;
t.modify(i, x);
}
for (int i = 1; i <= m; i++) {
int op, a, b;
std::cin >> op >> a >> b;
if (op == 1) {
t.modify(a, b);
} else {
std::cout << t.qry(b) - t.qry(a - 1) << '\n';
}
}
}
-
树状数组模板2,区间修改,单点查询。
query(int pos)查询的是区间[1, pos]的和,而题目要求一段区间加上某个值,因此考虑差分。用差分后的数组建树。修改时只需修改两端即可,事实上就是前缀和思想。
int main() {
int n, m;
std::cin >> n >> m;
fenwick<ll> t(n + 1);
std::vector<int> a(n + 1);
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
t.modify(i, a[i] - a[i - 1]);
}
for (int i = 1; i <= m; i++) {
int op;
std::cin >> op;
if (op == 1) {
int l, r, k;
std::cin >> l >> r >> k;
t.modify(l, k);
t.modify(r + 1, -k);
} else {
int x;
std::cin >> x;
std::cout << t.qry(x) << '\n';
}
}
}
-
区间修改区间查询
参考这位佬的博客吧qwq 链接🔗。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号