Catalan
原理:
令h(0)=1,h(1)=1,catalan 数满足递归式:
![]() (其中n>=2)
(其中n>=2)
另类递推公式:
![]()
该递推关系的解为:
![]() (n=1,2,3,...)
(n=1,2,3,...)
卡特兰数的应用实质上都是递归等式的应用
前几项为:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
应用:
问题描述:
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
问题分析:
我们先把这12个人从低到高排列,然后,选择6个人排在第一排,那么剩下的6个肯定是在第二排.
用0表示对应的人在第一排,用1表示对应的人在第二排,那么含有6个0,6个1的序列,就对应一种方案.
比如000000111111就对应着
第一排:0 1 2 3 4 5
第二排:6 7 8 9 10 11
010101010101就对应着
第一排:0 2 4 6 8 10
第二排:1 3 5 7 9 11
问题转换为,这样的满足条件的01序列有多少个。
观察1的出现,我们考虑这一个出现能不能放在第二排,显然,在这个1之前出现的那些0,1对应的人
要么是在这个1左边,要么是在这个1前面。而肯定要有一个0的,在这个1前面,统计在这个1之前的0和1的个数。
也就是要求,0的个数大于1的个数。
如果把0看成入栈操作,1看成出栈操作,就是说给定6个元素,合法的入栈出栈序列有多少个。
这就是catalan数,这里只是用于栈,等价地描述还有,二叉树的枚举、多边形分成三角形的个数、圆括弧插入公式中的方法数,其通项是c(2n, n)/(n+1)。
在<<计算机程序设计艺术>>,第三版,Donald E.Knuth著,苏运霖译,第一卷,508页,给出了证明:
问题大意是用S表示入栈,X表示出栈,那么合法的序列有多少个(S的个数为n)
显然有c(2n, n)个含S,X各n个的序列,剩下的是计算不允许的序列数(它包含正确个数的S和X,但是违背其它条件)。
在任何不允许的序列中,定出使得X的个数超过S的个数的第一个X的位置。然后在导致并包括这个X的部分序列中,以S代替所有的X并以X代表所有的S。结果是一个有(n+1)个S和(n-1)个X的序列。反过来,对一垢一种类型的每个序列,我们都能逆转这个过程,而且找出导致它的前一种类型的不允许序列。例如XXSXSSSXXSSS必然来自SSXSXXXXXSSS。这个对应说明,不允许的序列的个数是c(2n, n-1),因此an = c(2n, n) - c(2n, n-1)。
c(2n, n)/(n+1) = c(2n, n) - c(2n, n-1)
证明:
令1表示进栈,0表示出栈,则可转化为求一个2n位、含n个1、n个0的二进制数,满足从左往右扫描到任意一位时,经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有 个,下面考虑不满足要求的数目.
个,下面考虑不满足要求的数目.
考虑一个含n个1、n个0的2n位二进制数,扫描到第2m+1位上时有m+1个0和m个1(容易证明一定存在这样的情况),则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0,则对应一个n+1个0和n-1个1的二进制数。反之亦然(相似的思路证明两者一一对应)。
从而 。
。
Catalan 典型应用:
1、括号化问题。矩阵链乘: P=A1×A2×A3×……×An,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
一个有n个X和n个Y组成的字串,且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
将上例的X换成左括号,Y换成右括号,Cn表示所有包含n组括号的合法运算式的个数:
((())) ()(()) ()()() (())() (()())
2、将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域(划分线不交叉)的方法数?
一个凸多边形区域,有N条边,将其划分为三角形区域,问共有多少种分割方法。
(1)我们从最简单情况开始:N=3,f(3)=1;
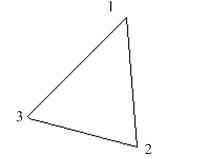
(2)当N=4,f(4)=2;
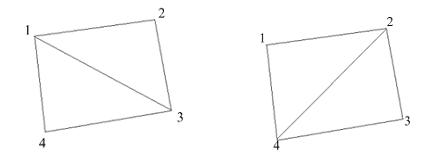
(3)N边时
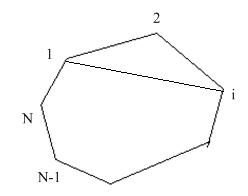
我们从节点1开始考虑,要想分割成三角形区域,1不能和与它相邻的点连接,所以1可以 连接3,4,...,N-1;
假设1连接i,则分割成的两个区域分别为i凸多边形和N+2-i凸多边形,即对于节点1,f1(N)=f(3)f(N+2-3)+f(4)f(N+2-4)+...+f(N-1)f(3);
N多边形共N个点,对应于每个点有f1(N)中分割方法,总的分割方法为f(N)=Nf1(N),但是每增加一条边,其连接两个点,所以在f(N)中有
一半是重复情况,所以最终的分割方法为:
![]()
类似:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
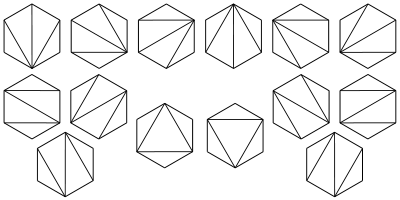
3、出栈次序问题。一个栈(无穷大)的进栈序列为1、2、3、...、n,有多少个不同的出栈序列?
类似:有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
类似:一位大城市的律师在他住所以北n个街区和以东n个街区处工作,每天她走2n个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
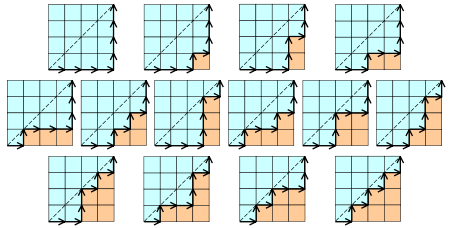
分析:对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
给定N个节点,能构成多少种形状不同的二叉树?
(1)n=0时,f(0)=1;
(2)n=1时,f(1)=1;
(3)n=2时,f(2)=4;
(4) f(N)=N(f(0)f(N-1)+f(1)f(N-2)+...+f(i)f(N-1-i)+...+f(N-1)f(0));采用递归的思想,f(i)f(N-1-i)中f(i)表示左子树有i个节点可构造的二叉树数目,f(N-1-i)表示右子树有N-1-i个节点可构造的二叉树数目;
两者相乘表示左右分别为i,N-1-i个节点时候这个大的二叉树的构造数目,又由于根节点的选择有N中选择方法,所以可得总的构造方法数目如式。

在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描,0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=1/(n+1)*c(2n,n)。
(这个公式的下标是从h(0)=1开始的)

1 //大数&&Catalan 2 /* 3 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 4 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 5 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 6 4861946401452, … 7 */ 8 #include<iostream> 9 #include<cstring> 10 #include<iomanip> 11 #include<algorithm> 12 using namespace std; 13 14 #define MAXN 9999 15 #define MAXSIZE 10 16 #define DLEN 4 17 18 class BigNum 19 { 20 private: 21 int a[500]; //可以控制大数的位数 22 int len; //大数长度 23 public: 24 BigNum(){ len = 1;memset(a,0,sizeof(a)); } //构造函数 25 BigNum(const int); //将一个int类型的变量转化为大数 26 BigNum(const char*); //将一个字符串类型的变量转化为大数 27 BigNum(const BigNum &); //拷贝构造函数 28 BigNum &operator=(const BigNum &); //重载赋值运算符,大数之间进行赋值运算 29 30 friend istream& operator>>(istream&, BigNum&); //重载输入运算符 31 friend ostream& operator<<(ostream&, BigNum&); //重载输出运算符 32 33 BigNum operator+(const BigNum &) const; //重载加法运算符,两个大数之间的相加运算 34 BigNum operator-(const BigNum &) const; //重载减法运算符,两个大数之间的相减运算 35 BigNum operator*(const BigNum &) const; //重载乘法运算符,两个大数之间的相乘运算 36 BigNum operator/(const int &) const; //重载除法运算符,大数对一个整数进行相除运算 37 38 BigNum operator^(const int &) const; //大数的n次方运算 39 int operator%(const int &) const; //大数对一个int类型的变量进行取模运算 40 bool operator>(const BigNum & T)const; //大数和另一个大数的大小比较 41 bool operator>(const int & t)const; //大数和一个int类型的变量的大小比较 42 43 void print(); //输出大数 44 }; 45 BigNum::BigNum(const int b) //将一个int类型的变量转化为大数 46 { 47 int c,d = b; 48 len = 0; 49 memset(a,0,sizeof(a)); 50 while(d > MAXN) 51 { 52 c = d - (d / (MAXN + 1)) * (MAXN + 1); 53 d = d / (MAXN + 1); 54 a[len++] = c; 55 } 56 a[len++] = d; 57 } 58 BigNum::BigNum(const char*s) //将一个字符串类型的变量转化为大数 59 { 60 int t,k,index,l,i; 61 memset(a,0,sizeof(a)); 62 l=strlen(s); 63 len=l/DLEN; 64 if(l%DLEN) 65 len++; 66 index=0; 67 for(i=l-1;i>=0;i-=DLEN) 68 { 69 t=0; 70 k=i-DLEN+1; 71 if(k<0) 72 k=0; 73 for(int j=k;j<=i;j++) 74 t=t*10+s[j]-'0'; 75 a[index++]=t; 76 } 77 } 78 BigNum::BigNum(const BigNum & T) : len(T.len) //拷贝构造函数 79 { 80 int i; 81 memset(a,0,sizeof(a)); 82 for(i = 0 ; i < len ; i++) 83 a[i] = T.a[i]; 84 } 85 BigNum & BigNum::operator=(const BigNum & n) //重载赋值运算符,大数之间进行赋值运算 86 { 87 int i; 88 len = n.len; 89 memset(a,0,sizeof(a)); 90 for(i = 0 ; i < len ; i++) 91 a[i] = n.a[i]; 92 return *this; 93 } 94 istream& operator>>(istream & in, BigNum & b) //重载输入运算符 95 { 96 char ch[MAXSIZE*4]; 97 int i = -1; 98 in>>ch; 99 int l=strlen(ch); 100 int count=0,sum=0; 101 for(i=l-1;i>=0;) 102 { 103 sum = 0; 104 int t=1; 105 for(int j=0;j<4&&i>=0;j++,i--,t*=10) 106 { 107 sum+=(ch[i]-'0')*t; 108 } 109 b.a[count]=sum; 110 count++; 111 } 112 b.len =count++; 113 return in; 114 115 } 116 ostream& operator<<(ostream& out, BigNum& b) //重载输出运算符 117 { 118 int i; 119 cout << b.a[b.len - 1]; 120 for(i = b.len - 2 ; i >= 0 ; i--) 121 { 122 cout.width(DLEN); 123 cout.fill('0'); 124 cout << b.a[i]; 125 } 126 return out; 127 } 128 129 BigNum BigNum::operator+(const BigNum & T) const //两个大数之间的相加运算 130 { 131 BigNum t(*this); 132 int i,big; //位数 133 big = T.len > len ? T.len : len; 134 for(i = 0 ; i < big ; i++) 135 { 136 t.a[i] +=T.a[i]; 137 if(t.a[i] > MAXN) 138 { 139 t.a[i + 1]++; 140 t.a[i] -=MAXN+1; 141 } 142 } 143 if(t.a[big] != 0) 144 t.len = big + 1; 145 else 146 t.len = big; 147 return t; 148 } 149 BigNum BigNum::operator-(const BigNum & T) const //两个大数之间的相减运算 150 { 151 int i,j,big; 152 bool flag; 153 BigNum t1,t2; 154 if(*this>T) 155 { 156 t1=*this; 157 t2=T; 158 flag=0; 159 } 160 else 161 { 162 t1=T; 163 t2=*this; 164 flag=1; 165 } 166 big=t1.len; 167 for(i = 0 ; i < big ; i++) 168 { 169 if(t1.a[i] < t2.a[i]) 170 { 171 j = i + 1; 172 while(t1.a[j] == 0) 173 j++; 174 t1.a[j--]--; 175 while(j > i) 176 t1.a[j--] += MAXN; 177 t1.a[i] += MAXN + 1 - t2.a[i]; 178 } 179 else 180 t1.a[i] -= t2.a[i]; 181 } 182 t1.len = big; 183 while(t1.a[len - 1] == 0 && t1.len > 1) 184 { 185 t1.len--; 186 big--; 187 } 188 if(flag) 189 t1.a[big-1]=0-t1.a[big-1]; 190 return t1; 191 } 192 193 BigNum BigNum::operator*(const BigNum & T) const //两个大数之间的相乘运算 194 { 195 BigNum ret; 196 int i,j,up; 197 int temp,temp1; 198 for(i = 0 ; i < len ; i++) 199 { 200 up = 0; 201 for(j = 0 ; j < T.len ; j++) 202 { 203 temp = a[i] * T.a[j] + ret.a[i + j] + up; 204 if(temp > MAXN) 205 { 206 temp1 = temp - temp / (MAXN + 1) * (MAXN + 1); 207 up = temp / (MAXN + 1); 208 ret.a[i + j] = temp1; 209 } 210 else 211 { 212 up = 0; 213 ret.a[i + j] = temp; 214 } 215 } 216 if(up != 0) 217 ret.a[i + j] = up; 218 } 219 ret.len = i + j; 220 while(ret.a[ret.len - 1] == 0 && ret.len > 1) 221 ret.len--; 222 return ret; 223 } 224 BigNum BigNum::operator/(const int & b) const //大数对一个整数进行相除运算 225 { 226 BigNum ret; 227 int i,down = 0; 228 for(i = len - 1 ; i >= 0 ; i--) 229 { 230 ret.a[i] = (a[i] + down * (MAXN + 1)) / b; 231 down = a[i] + down * (MAXN + 1) - ret.a[i] * b; 232 } 233 ret.len = len; 234 while(ret.a[ret.len - 1] == 0 && ret.len > 1) 235 ret.len--; 236 return ret; 237 } 238 int BigNum::operator %(const int & b) const //大数对一个int类型的变量进行取模运算 239 { 240 int i,d=0; 241 for (i = len-1; i>=0; i--) 242 { 243 d = ((d * (MAXN+1))% b + a[i])% b; 244 } 245 return d; 246 } 247 BigNum BigNum::operator^(const int & n) const //大数的n次方运算 248 { 249 BigNum t,ret(1); 250 int i; 251 if(n<0) 252 exit(-1); 253 if(n==0) 254 return 1; 255 if(n==1) 256 return *this; 257 int m=n; 258 while(m>1) 259 { 260 t=*this; 261 for( i=1;i<<1<=m;i<<=1) 262 { 263 t=t*t; 264 } 265 m-=i; 266 ret=ret*t; 267 if(m==1) 268 ret=ret*(*this); 269 } 270 return ret; 271 } 272 bool BigNum::operator>(const BigNum & T) const //大数和另一个大数的大小比较 273 { 274 int ln; 275 if(len > T.len) 276 return true; 277 else if(len == T.len) 278 { 279 ln = len - 1; 280 while(a[ln] == T.a[ln] && ln >= 0) 281 ln--; 282 if(ln >= 0 && a[ln] > T.a[ln]) 283 return true; 284 else 285 return false; 286 } 287 else 288 return false; 289 } 290 bool BigNum::operator >(const int & t) const //大数和一个int类型的变量的大小比较 291 { 292 BigNum b(t); 293 return *this>b; 294 } 295 296 void BigNum::print() //输出大数 297 { 298 int i; 299 cout << a[len - 1]; 300 for(i = len - 2 ; i >= 0 ; i--) 301 { 302 cout.width(DLEN); 303 cout.fill('0'); 304 cout << a[i]; 305 } 306 cout << endl; 307 } 308 int main() 309 { 310 int i,n; 311 BigNum x[101]; //定义大数的对象数组 312 x[0]=1; 313 for(i=1;i<101;i++) 314 x[i]=x[i-1]*(4*i-2)/(i+1); 315 while(scanf("%d",&n)==1 && n!=-1) 316 { 317 x[n].print(); 318 } 319 }




