799. 香槟塔 ----- 动态规划、模拟、逆向

我们把玻璃杯摆成金字塔的形状，其中 第一层 有 1 个玻璃杯， 第二层 有 2 个，依次类推到第 100 层，每个玻璃杯 (250ml) 将盛有香槟。

从顶层的第一个玻璃杯开始倾倒一些香槟，当顶层的杯子满了，任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了，就会等流量的流向它们左右两边的杯子，依次类推。（当最底层的玻璃杯满了，香槟会流到地板上）

例如，在倾倒一杯香槟后，最顶层的玻璃杯满了。倾倒了两杯香槟后，第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后，第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后，第三层中间的玻璃杯盛放了一半的香槟，他两边的玻璃杯各自盛放了四分之一的香槟，如下图所示。

 

 

 

 

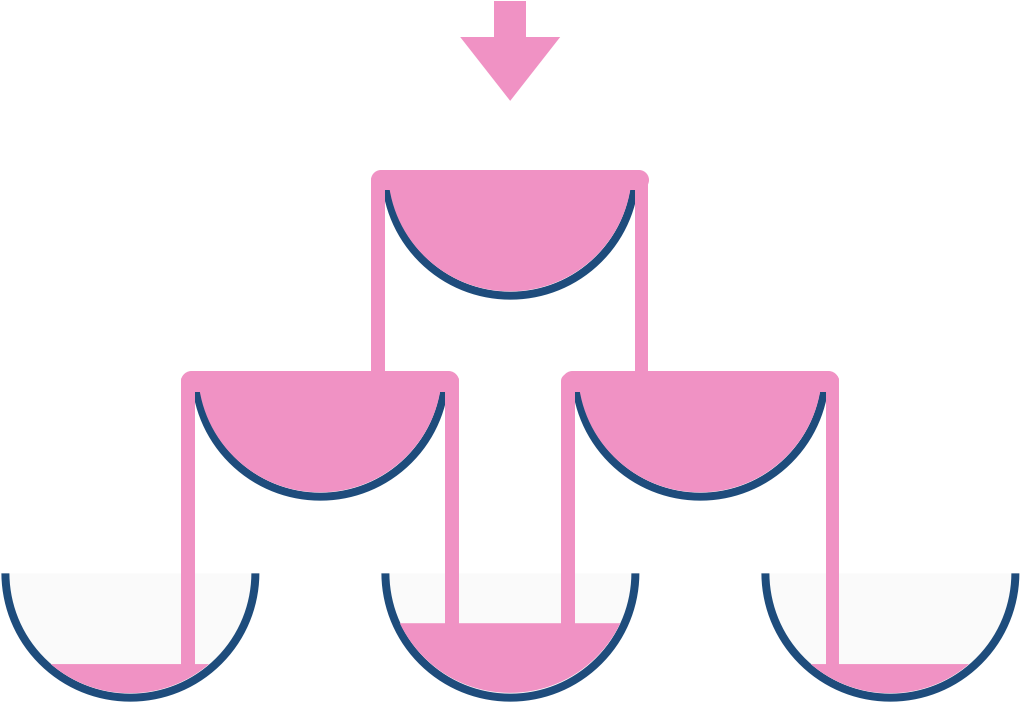
现在当倾倒了非负整数杯香槟后，返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例（ i 和 j 都从0开始）。

 

示例 1:
输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.00000
解释: 我们在顶层（下标是（0，0））倒了一杯香槟后，没有溢出，因此所有在顶层以下的玻璃杯都是空的。

示例 2:
输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.50000
解释: 我们在顶层（下标是（0，0）倒了两杯香槟后，有一杯量的香槟将从顶层溢出，位于（1，0）的玻璃杯和（1，1）的玻璃杯平分了这一杯香槟，所以每个玻璃杯有一半的香槟。
示例 3:

输入: poured = 100000009, query_row = 33, query_glass = 17
输出: 1.00000
 

提示:

0 <= poured <= 109
0 <= query_glass <= query_row < 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/champagne-tower
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

逆向：

class Solution {
public:
    double champagneTower(int poured, int query_row, int query_glass) {
        double dp[101][101] = {0.0};
        dp[1][1] = poured; // 为了防止越界，下标（0,0）的酒杯我们存放在dp[1][1]的位置上
        for (int row = 2; row <= query_row + 1; row++) {
            for (int column = 1; column <= row; column++) {
                dp[row][column] = max(dp[row - 1][column - 1] - 1, 0.0) / 2 + max(dp[row - 1][column] - 1, 0.0) / 2;
            }
        }
        return min(dp[query_row + 1][query_glass + 1], 1.0);
    }
};

 

正向：

class Solution {
public:
    double champagneTower(int poured, int query_row, int query_glass) {
        double dp[101][101] = {0.0};
        // 所有的酒都先装入第一个杯子
        dp[0][0] = poured;
        // 从上到下遍历所有杯子
        for (int i = 0; i <= query_row; i++) {
            for (int j = 0; j <= i; j++) {
                // 如果这个杯子中的酒能装满
                if (dp[i][j] >= 1) {
                    double remain = dp[i][j] - 1; // 剩余的酒
                    dp[i][j] = 1; // 这个杯子装满了
                    
                    // 它下面的两个杯子均分剩余的酒
                    dp[i + 1][j] += remain / 2;
                    dp[i + 1][j + 1] += remain / 2;
                }
            }
        }
        return dp[query_row][query_glass];
    }
};