124. 二叉树中的最大路径和 ---- 最小树分类、递归

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

 

示例 1：

 

 

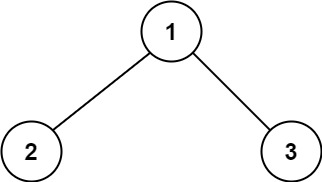
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：

 

 

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42
 

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/binary-tree-maximum-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

最小树分类 + 递归：

　　不用看官方题解，那么复杂。 所有树的题目，都想成一颗只有根、左节点、右节点 的小树。然后一颗颗小树构成整棵大树，所以只需要考虑这颗小树即可。接下来分情况， 按照题意：一颗三个节点的小树的结果只可能有如下6种情况：

1. 根 + 左 + 右
2. 根 + 左
3. 根 + 右
4. 根
5. 左
6. 右

好了，分析上述6种情况， 只有 2,3,4 可以向上累加，而1,5,6不可以累加（这个很好想，情况1向上累加的话，必然出现分叉，情况5和6直接就跟上面的树枝断开的，没法累加），所以我们找一个全局变量存储 1,5,6这三种不可累加的最大值， 另一方面咱们用遍历树的方法求2,3,4这三种可以累加的情况。 最后把两类情况得到的最大值再取一个最大值即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int max_sum = -1000;
    int maxadd(TreeNode* root) {
        if (!root) return -1000;
        int left = maxadd(root->left);
        int right = maxadd(root->right);   
        max_sum = max ({max_sum, root->val + left + right, left, right}); // 情况1,5,6，不累加直接放变量里暂存
        return max({root->val, root->val + left, root->val + right});  // 情况2,3,4 ，累加需要递归
    }
    int maxPathSum(TreeNode* root) {
        if (!root->left && !root->right) return root->val;
        int act_max = maxadd(root);
        return max(max_sum, act_max);      
    }
};