114. 二叉树展开为链表 ----- 子树拼接类莫里斯Morris 算法、变相后序遍历解决右子树丢失问题、先序遍历栈储存右结点解决右子树丢失问题

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
 

示例 1：

 

 

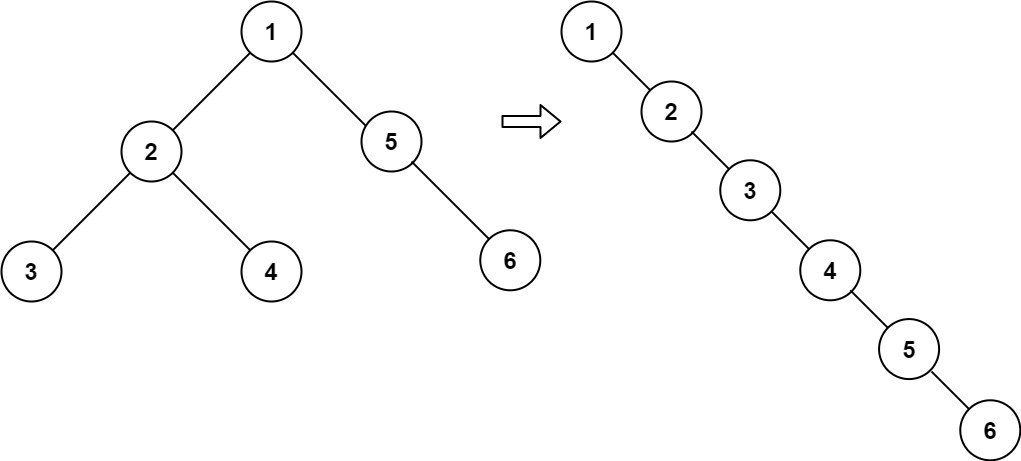
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [0]
输出：[0]
 

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
 

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/flatten-binary-tree-to-linked-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

子树拼接Morris：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        while (root) { 
        //左子树为 null，直接考虑下一个节点
        if (!root->left) {
            root = root->right;
        } 
        else {
            // 找左子树最右边的节点
            TreeNode* pre = root->left;
            while (pre->right != nullptr) {
                pre = pre->right;
            } 
            //将原来的右子树接到左子树的最右边节点
            pre->right = root->right;
            // 将左子树插入到原本右子树的地方
            root->right = root->left;
            root->left = nullptr;
            // 考虑下一个节点
            root = root->right;
        }
        }
    }
};

 变相后序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* last = nullptr;
    void flatten(TreeNode* root) {
        if (root == nullptr) return;
        flatten(root->right);
        flatten(root->left);
        root->right = last;
        root->left = nullptr;
        last = root;
    }
};

先序遍历+栈：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    public:
        void flatten(TreeNode* root) { 
        if (!root){
            return;
        }
        stack<TreeNode*> s; // 创建栈 保存左子树结点
        s.push(root); //入栈
        TreeNode* pre = nullptr;
        while (!s.empty()) {
            TreeNode* temp = s.top(); // 栈顶保存
            s.pop(); //出栈
            /***********修改的地方*************/
            if(pre){
                pre->right = temp; // 右结点 先连接栈里储存的左结点
                pre->left = nullptr; // 左结点置空
            }
            /********************************/
            if (temp->right){
                s.push(temp->right); // 右结点入栈
            }
            if (temp->left){
                s.push(temp->left); // 左结点入栈
            } 
            /***********修改的地方*************/
            pre = temp; // 处理下一节点
            /********************************/
        }
    }
};

先序遍历 递归：

class Solution {
public:
    void flatten(TreeNode* root) {
        vector<TreeNode*> l;
        preorderTraversal(root, l); // 先序遍历 结果存进l
        int n = l.size();
        for (int i = 1; i < n; i++) {
            TreeNode *prev = l.at(i - 1), *curr = l.at(i); // 创建先后结点
            prev->left = nullptr; // 先结点左子树置空
            prev->right = curr; // 先结点右子树 为后结点（先序遍历顺序的后一位就是左结点）
        }
    }

    void preorderTraversal(TreeNode* root, vector<TreeNode*> &l) {
        if (root != NULL) {
            l.push_back(root);
            preorderTraversal(root->left, l);
            preorderTraversal(root->right, l);
        }
    }
};