KMP 算法理解与掌握 边学边写 ------字符串匹配问题（父串中寻找字串）

1.初遇KMP算法：

　　在今天做 leetcode每日一题的时候 遇上了这么一道题：

　　　　　　　

　　求一个字符串在另一个字符串中连续重复出现的次数。

这道题 可以用 BF 穷举暴力解题，但是力扣官方题解中给出了时间复杂度更小的方法

其中使用到了KMP算法。

　　KMP算法：

　　KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n）

　　在自己理解的过程中，发现许多文章和博客对于KMP算法中 NEXT[ ] 数组的实现以及内涵意义说的并不是十分清晰，以至于在浏览完几篇文章后，只是粗略了解了KMP算法如何使用以及实现的过程。

　　下面将用笔者自己的理解，尝试在写这篇博客的过程中帮助自己更加深入的理解和掌握KMP算法的内涵：

---

---

 

2.KMP算法的认识：

1.适用问题及算法背景：

　　KMP算法被广泛的用于解决字符串匹配问题，对于一个等待匹配的主串，和一个用来匹配的模式串，我们可以使用KMP算法去实现快速的匹配与查找，主串中与模式串相同的部分出现的位置，以及出现的次数。

　　对于传统的字符串匹配，在KMP方法还未被发明之前，要解决这个问题几乎都离不开，“从初始位置开始遍历主串，在遍历过程中与模式串一一对应判断每一位字符是否匹配，如果途中出现匹配失败的情况，则需要从主串开始匹配的初始位置的下一位开始重新对主串进行遍历，然后重复上方的与模式串一一对应判断是否匹配的过程，直到完成一次与模式串的完整成功匹配，或者已经对主串遍历完成但仍未匹配成功。" 这整个暴力枚举过程被称作------

　　"BF"算法（Brute-Force）

如图:

 

 

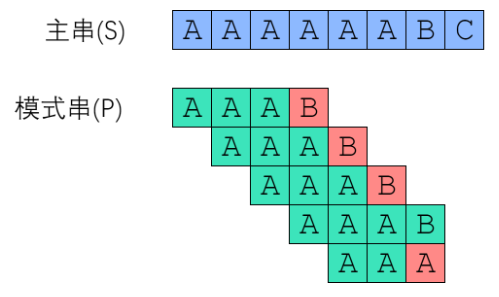
　　然而，从刚才对整个枚举匹配的过程的描述中，我们将主串的大小命名为M，模式串的大小命名为N，我们可以算出，在最坏的情况下，如果主串与模式串只有最后一位不同，那么我们需要从主串的初始位置开始，从初始位置一直到（M - N）位置的每一次遍历都需要匹配N次，再加上主串剩下的字符串与模式串的一次遍历匹配，总共需要遍历M - N + 1次，时间复杂度为O(N * (M - N + 1))，但是，在大部分实际场景下待匹配的主串的大小一般远大于模式串，即 M>>N，所以最终BF算法的时间复杂度为 O(N * M)。

---

 

　　改进与思考：

　　这个时间复杂度看起来并没有那么好。

　　所以，我们尝试分析BF算法 的实现过程中，有无一些可以改进的地方，或者说能够看出来是在做”浪费“的操作的地方。

　　BF算法的核心是枚举，是在每一次发生”不匹配“时，主串退回到上一次匹配的初始位置，然后往后挪一位开始新的匹配，相当于每一次发生”不匹配“后只比上一次”进步“了一点，但是我们通过下面图片的例子明显观察到在第一次发生”不匹配“后，只有主串的第6个位置上的 ' ？' ，与模式串的第6个位置上的 ‘d ’，是不同的，而模式串之前的 'abcab'是成功匹配的，那么，观察 ‘abcab’这一串已经成功匹配的字符串，如果我们能够在这个属于我们匹配一次后留下来的 “经验” 中 发现一些“宝藏”，找到其中的一些规律，就能帮助我们在下一次匹配开始时多获得一些 ”进步“ ，那么我们就可以避免多余的 “重蹈覆辙”。

 

 

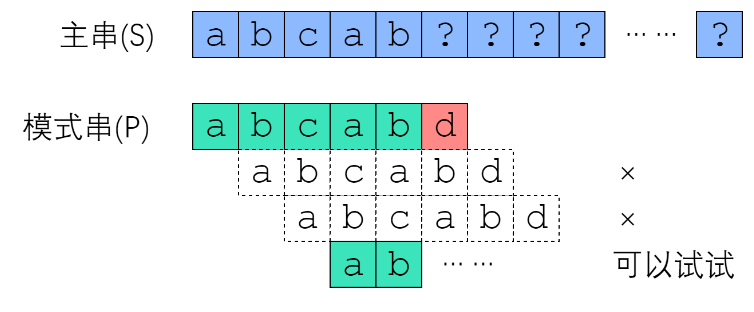
 　　我们发现 ‘abcab’ 这一字符串中，有一个明显的特征----- 它的最前面两个字符 ”ab“，与最后两个字符 ”ab“，完全相等，那么我们直接在下一次对主串的遍历时，不选择从初始位置的下一位开始，而是选择从末尾的 "ab" 开始（从挪一位变成挪三位），因为 “abcab” 是一个完全可以和模式串成功匹配的字符串，那么从“abcab”的初始位置 ’a‘ 开始一直到结束的 'b'，按顺序得到的所有字符串子集，如：“a”,"ab","abc","abca","abcab","b","bc"......"ab","b"，都是可以保证能成功匹配到模式串上的，但是我们需要的是其中能从模式串的头部开始就成功匹配的那些部分（而不是只能对应模式串中间的某一部分），而且这部分应该越大越好，模式串的起始字符为 ”a“,因此我们只能选择除了第一个"a",以外的其他 “a” 作为开始才能有希望满足从一开始就成功匹配模式串，按照这个思路，依次去找，我们最后要找的应该是：在 “abcab” 中从头部开始找到一个最长的能和 “abcab” 尾部（后缀）一模一样的 “ 前缀 ” 。这一对相同的前缀和后缀 就是我们最需要的 “宝藏”。

　　在上图中， “abcab” 的 “宝藏” 是 ”ab“,我们把这个前缀（或者后缀）“ ab ” 的长度 2 称为 “abcab” 的最大前缀/后缀 公共长度。

　　我们完全可以在发生一次失败匹配后，把得到的已经确认的成功匹配的字符串 去做一次处理，得到这个字符串的 “最大前缀/后缀公共长度” （后续简称为‘最大公共长’）我们把这个长度命名为 ‘ L ’。

　　再每一次得到 L 后，我们都将下一次对主串的新的遍历匹配的起始位置，设置在原初始位置的L个之后，就像刚刚的例子：（如图）

 

 

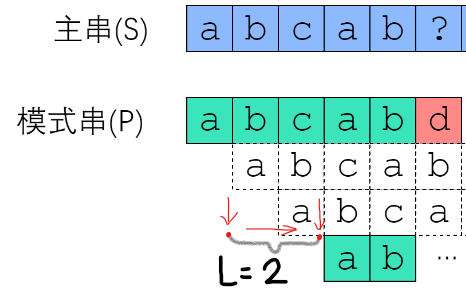
 　　至此，我们从一开始的 BF 枚举暴力算法中每次只进步一点点，经过上面的分析变成了，每一次可以进步 ' L' 。

　　既然我们知道，只要在一次失败匹配后，得到 最大公共长度 ----- L，我们就能前进 ' L '，那么如何去求得每一次的 L 呢?

---

 

　　求每一个最大公共长（求next数组）：

　　我们带着这个疑惑，先去认识一个新的数组 next 数组 ，它有一个理解起来作用更加直白的名称：部分匹配表(Partial Match Table)：一个next数组就对应一个PMT匹配表

如图：对于一个模式串 “ abababca ” 它的PTM表如下

 

 

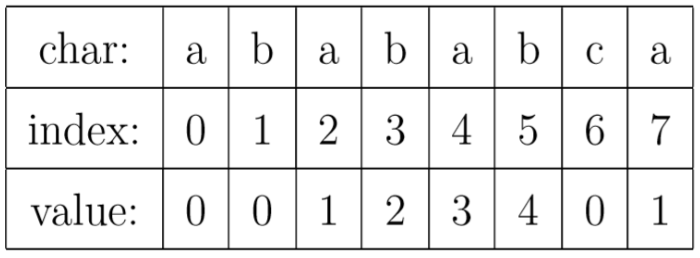
 　　其中的 value 值就是我们之前提到的 最大公共长 L。

　　而其中对应的next数组为next[8] = {0, 0, 1, 2, 3, 4, 0, 1} 

　　回到一开始的问题，到底怎么求得 next数组的值呢？

　　我们先来浅浅尝试一下，设模式串为 p 以及一个next 数组，如果已知 p 的next [ x - 1] = now，怎么求得next [ x ]。

　　首先，我们知道 next [ x - 1] = now， 意味着在 p 中，从p[ 0 ] 到 p[ x - 1 ] 位置的最大公共长 L 为 now，那么第一种情况，如果下一个位置，即 p[ x ] 与 p [ now ] 相等，那么说明 因为p [ x ]的存在，导致最大公共长 L +1，即next [ x ] = now + 1

　　如图（以 now = 2 为例）：

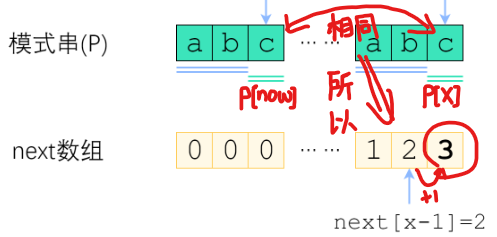
　　第二种情况 就是 如果下一个位置，即 p [ x ] 与 p [ now ] 不相等，那么因为 p [ x ]的存在，最大公共长应该会变小，而具体变成多少，取决于长度为 now 的字符串的公共最大长 L_now，为什么是这样呢，因为我们其实在刚刚比较 p [ x ] 与 p [ now ] 是否相等的过程中，是在默默的进行一次新的字符串匹配!!!，如果不相等，说明发生了匹配失败，那么就回到我们之前讲到的找宝藏的过程！！cool!!😎

　　所以我们就应该在这里再做一次找最大公共长的操作，而这个‘L_now’ 就等于next [ now - 1], 这个时候我们就要倒过来比较 p [ x ] 与 p [ L_now ] 是否相等。

　　如图：(以新字符串“ abcab ”, L _ now = 2 为例)

 

 

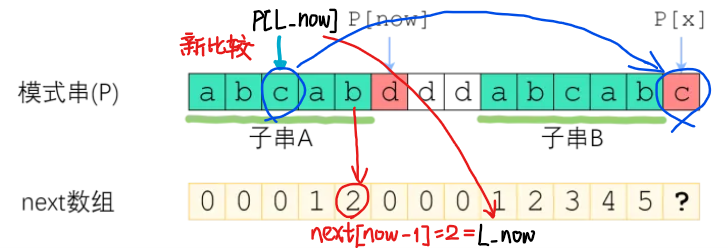
 　　此时， p [ x ] 与 p [ L_now ] 相等，所以我们得到，next[ x ] = L_now + 1 = 3。

当然如果 p [ x ] 与 p [ L_now ] 不相等，那么将继续寻找下一个新的 L_now, 继续让 p [ x ] 与 p [ L_now ] 比较，直到p [ x ] 与 p [ L_now ] 相等就令next[ x ] = L_now + 1 ，或者 公共最大长L_now = 0 则 next[ x ] = 0。

　　整个过程是一个递推过程，实际在求next数组的过程中，需要在next[0] = 0的条件下去求next[ x ]。

---

 

 

求next[ x ]的python代码如下：

模式串大小为 n，时间复杂度为O(n) 

 

 

 

---

 

 

　　KMP算法的实现 ：

　　 现在我们已经求得了整个模式串的 next数组，接下来我们终于要开始真正应用next数组，开始实现我们的KMP算法：

来一个形象生动的图举例：

 

 

 

 

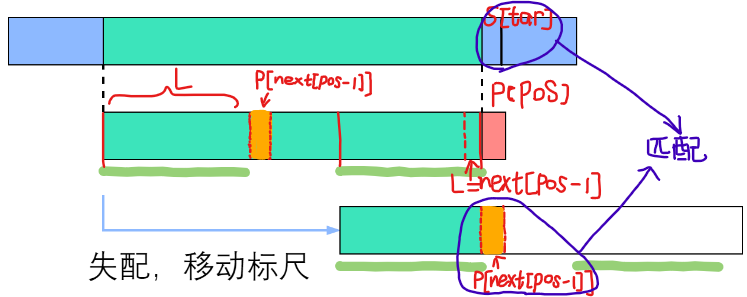
 　　描述为：如果在 s[star] 和 p[pos] 发生一次失败匹配后，根据 L = next[pos - 1]，找到模式串前缀中最大公共长之后的位置，以该位置为下一次匹配的新起点，即 pos = next[pos - 1]，再比较 p [next[pos - 1]] 与 s[star]，直到匹配成功 或 next[pos - 1] = 0就从模式串的第一个字符，重新开始匹配。

　　字符串匹配的python代码如下：

 

 

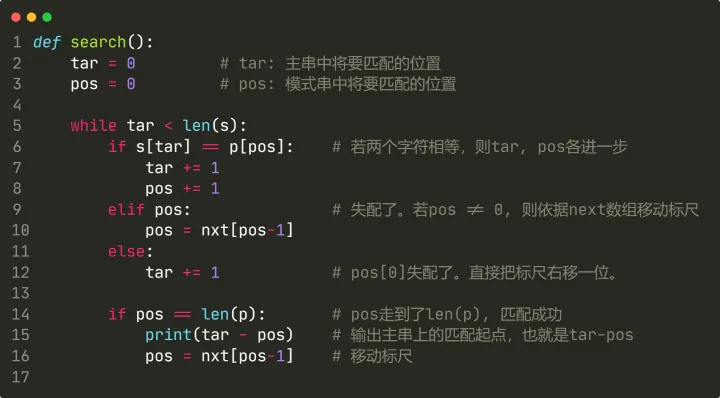
　　主串的大小为m， 模式串的大小为n，当最坏情况主串与模式串只有最后一位不相等时，该过程的时间复杂度为O(m/n-1 * n) ---> O(m) ，加上创建next数组的时间复杂度O(n)

KMP算法的总时间复杂度为————

　　O (m + n)

---

　　总结：

　　至此我们完成了对KMP算法的掌握，成功理解了其中的原理并实现了KMP算法，知道KMP算法的总时间复杂度为O (m + n)

　　那么请之后遇上 关于字符串的匹配问题 请务必使用KMP算法！

　　完结🎇！