[leetcode 周赛 160] 1240 铺瓷砖

1240 Tiling a Rectangle with the Fewest Squares 铺瓷砖

问题描述

你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。

房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。

假设正方形瓷砖的规格不限，边长都是整数。

请你帮设计师计算一下，最少需要用到多少块方形瓷砖？

示例 1：

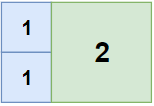
输入： n = 2, m = 3
输出： 3
**解释：**3 块地砖就可以铺满卧室。
2 块 1x1 地砖
1 块 2x2 地砖

示例 2：

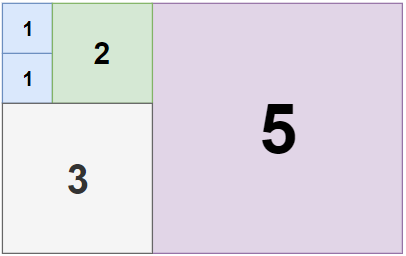
输入： n = 5, m = 8
输出： 5

示例 3：

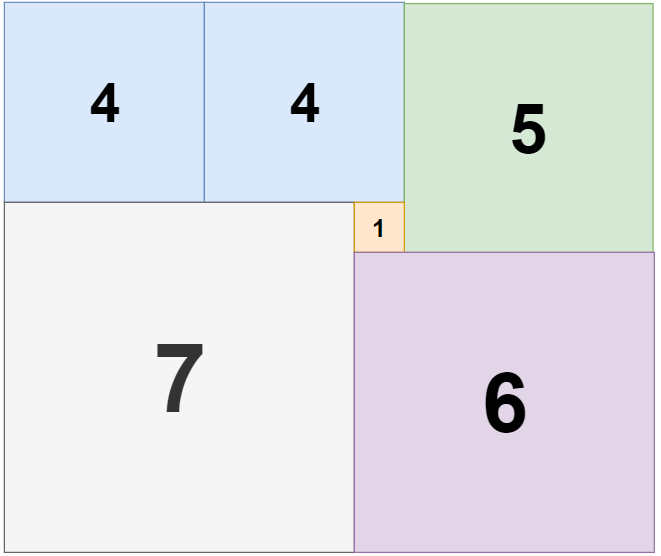
输入： n = 11, m = 13
输出： 6

提示：

• 1 <= n <= 13
• 1 <= m <= 13

思路

• 读题
  给定固定面积的房间N*M, 使用正方形瓷砖刚好填满, 瓷砖长度不定, 要求使用瓷砖数量最少

贪心思想+动规实现+特例排除

• 贪心
  每次选取最大长度的正方形分割(当前最优解), 以此将区块分成两份, 其中一份继续贪心的选取最大长度的正方形分割
• 动规
  每个区块可以分成两个小区块, 小区块又可以继续划分 --> 小区块的最优解合并成大区块的最优解
• 特例
  11*13这个区块 最优解不能完全分割成两个不相关的区块

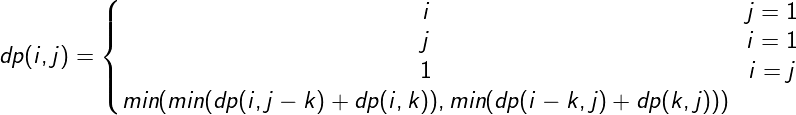
• 一般区块的最优解分3种情况:
  1. N=1 或者 M=1 即只能平铺1*1的方块 M或N个
  2. N=M 直接一步到位 铺上N*N的方块 1个
  3. 其他情况 将区块横着切分或者竖着切分 找到最小的那个方案

打表法

因为运算的数据量不大 13*13
可以手动生成全局答案

[1,  2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
[2,  1, 3, 2, 4, 3, 5, 4, 6, 5,  7,  6,  8]
[3,  3, 1, 4, 4, 2, 5, 5, 3, 6,  6,  4,  7]
[4,  2, 4, 1, 5, 3, 5, 2, 6, 4,  6,  3,  7]
[5,  4, 4, 5, 1, 5, 5, 5, 6, 2,  6,  6,  6]
[6,  3, 2, 3, 5, 1, 5, 4, 3, 4,  6,  2,  6]
[7,  5, 5, 5, 5, 5, 1, 7, 6, 6,  6,  6,  6]
[8,  4, 5, 2, 5, 4, 7, 1, 7, 5,  6,  3,  6]
[9,  6, 3, 6, 6, 3, 6, 7, 1, 6,  7,  4,  7]
[10, 5, 6, 4, 2, 4, 6, 5, 6, 1,  6,  5,  7]
[11, 7, 6, 6, 6, 6, 6, 6, 7, 6,  1,  7,  6]
[12, 6, 4, 3, 6, 2, 6, 3, 4, 5,  7,  1,  7]
[13, 8, 7, 7, 6, 6, 6, 6, 7, 7,  6,  7,  1]

代码实现

动态规划

public class Solution {
    private static int size = 13;
    private static int[][] dp = new int[size + 1][size + 1];

    static {
        // 初始化为-1 表示没有被修改
        for (int i = 1; i <= size; i++) {
            Arrays.fill(dp[i], -1);
        }

        for (int i = 1; i <= size; i++) {
            // i*1 or 1*i 面积的铺瓷砖数量
            dp[i][1] = i;
            dp[1][i] = i;
            // i*i 面积的铺瓷砖数量
            dp[i][i] = 1;
        }

        // 唯一的特殊情况 11*13 or 13*11 面积的铺瓷砖数量 不符合贪心规则
        int specialCaseW = 11, specialCaseH = 13, specialCaseR = 6;
        dp[specialCaseH][specialCaseW] = specialCaseR;
        dp[specialCaseW][specialCaseH] = specialCaseR;
    }

    public int tilingRectangle(int n, int m) {
        return helper(n, m);
    }

    private int helper(int n, int m) {
        if (dp[n][m] != -1) {
            return dp[n][m];
        }

        // 最大分块 n*m个1*1方块
        int res = n * m, tmp;
        // 横着切 
        for (int i = 1; i < n; i++) {
            tmp = helper(i, m) + helper(n - i, m);
            res = Math.min(res, tmp);
        }
        // 竖着切
        for (int i = 1; i < m; i++) {
            tmp = helper(n, i) + helper(n, m - i);
            res = Math.min(res, tmp);
        }

        // 备忘录 n*m == m*n
        dp[n][m] = dp[m][n] = res;
        return res;
    }
}

参考资源

第 160 场周赛 全球排名
力扣周赛录屏-leetcode-weekly-contest-160