[leetcode 周赛 160] 1237 找出给定方程的正整数解

1237 Find Positive Integer Solution for a Given Equation 找出给定方程的正整数解

问题描述

给出一个函数 f(x, y) 和一个目标结果 z，请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。

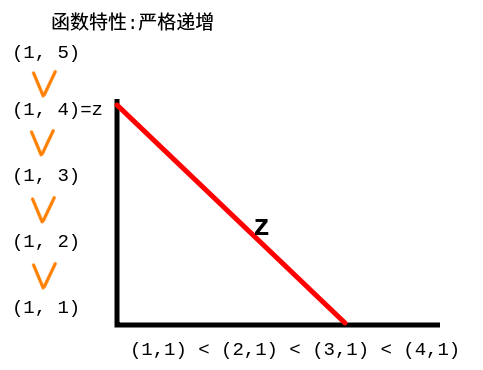
给定函数是严格单调的，也就是说：

• f(x, y) < f(x + 1, y)
• f(x, y) < f(x, y + 1)

函数接口定义如下：

interface CustomFunction {
public:
  // Returns positive integer f(x, y) for any given positive integer x and y.
  int f(int x, int y);
};

如果你想自定义测试，你可以输入整数 function_id 和一个目标结果 z 作为输入，其中 function_id 表示一个隐藏函数列表中的一个函数编号，题目只会告诉你列表中的 2 个函数。

你可以将满足条件的 结果数对 按任意顺序返回。

示例 1：

输入： function_id = 1, z = 5
输出： [[1,4],[2,3],[3,2],[4,1]]
解释： function_id = 1 表示 f(x, y) = x + y

示例 2：

输入： function_id = 2, z = 5
输出： [[1,5],[5,1]]
解释： function_id = 2 表示 f(x, y) = x * y

提示：

• 1 <= function_id <= 9
• 1 <= z <= 100
• 题目保证 f(x, y) == z 的解处于 1 <= x, y <= 1000 的范围内。
• 在 1 <= x, y <= 1000 的前提下，题目保证 f(x, y) 是一个 32 位有符号整数。

思路

• 读题
  给定一个黑盒函数, 它的特点是严格递增, 找到函数结果为输入值的(x, y)对
  

暴力法

读题可知, 函数由输入结果z划分, 固定x值, 遍历y值, 直到找到结果则终止, x+1进入下一次遍历

暴力法+二分

读题可知, 每个x值的直线与结果z直线只有一个交点, 而这个交点的y值符合二分遍历的特性
固定x值: (x, my-1) < (x, my)=z < (x, my+1)
(二分在一个有序数组中查找特定元素)

代码实现

暴力法

class Solution {
    public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {
        List<List<Integer>> ans = new ArrayList<>();

        // x,y 的取值范围[1, 1000]
        int size = 1000;
        for (int x = 1; x <= size; x++) {
            for (int y = 1; y <= size; y++) {
                int cur = customfunction.f(x, y);
                if (cur == z) {
                    ans.add(Arrays.asList(x, y));
                } else if (cur > z) {
                    // 函数是严格单调
                    break;
                }
            }
        }

        return ans;
    }
}

暴力+二分

class Solution {
    public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {
        // 符合一个二分的特性 最终结果z: 固定某一x (x, my-1)<(x, my)=z<(x, my+1)
        int size = 1000;
        List<List<Integer>> ans = new ArrayList<>();
        for (int x = 1; x < size; x++) {
            if (customfunction.f(x, 1) > z) {
                break;
            }
            // 通过二分查找 在一个`递增数列`中
            int lo = 1, hi = size;
            while (lo < hi) {
                int my = (lo + hi) / 2;
                int cur = customfunction.f(x, my);
                if (cur > z) {
                    hi = my;
                } else if (cur < z) {
                    lo = my + 1;
                } else {
                    // cur == z 查找到 直接跳出
                    ans.add(Arrays.asList(x, my));
                    break;
                }
            }
        }

        return ans;
    }
}

参考资源

第 160 场周赛 全球排名