[leetcode] 682 Baseball Game 棒球比赛
题目:682. 棒球比赛
你现在是棒球比赛记录员。
给定一个字符串列表,每个字符串可以是以下四种类型之一:
整数(一轮的得分):直接表示您在本轮中获得的积分数。"+"(一轮的得分):表示本轮获得的得分是前两轮有效 回合得分的总和。"D"(一轮的得分):表示本轮获得的得分是前一轮有效 回合得分的两倍。"C"(一个操作,这不是一个回合的分数):表示您获得的最后一个有效 回合的分数是无效的,应该被移除。
每一轮的操作都是永久性的,可能会对前一轮和后一轮产生影响。
你需要返回你在所有回合中得分的总和。
- 示例 1:
输入: ["5","2","C","D","+"]
输出: 30
解释:
第1轮:你可以得到5分。总和是:5。
第2轮:你可以得到2分。总和是:7。
操作1:第2轮的数据无效。总和是:5。
第3轮:你可以得到10分(第2轮的数据已被删除)。总数是:15。
第4轮:你可以得到5 + 10 = 15分。总数是:30。
- 示例 2:
输入: ["5","-2","4","C","D","9","+","+"]
输出: 27
解释:
第1轮:你可以得到5分。总和是:5。
第2轮:你可以得到-2分。总数是:3。
第3轮:你可以得到4分。总和是:7。
操作1:第3轮的数据无效。总数是:3。
第4轮:你可以得到-4分(第三轮的数据已被删除)。总和是:-1。
第5轮:你可以得到9分。总数是:8。
第6轮:你可以得到-4 + 9 = 5分。总数是13。
第7轮:你可以得到9 + 5 = 14分。总数是27。
- 注意:
输入列表的大小将介于1和1000之间。
列表中的每个整数都将介于-30000和30000之间。
思路
每一轮的操作(数字,“+”相加, “C”消除, “D”翻倍),都将影响与答案相关的有效数字
其中:
- 数字 -- 影响本轮;
- “+”、“D” -- 依赖上一轮有效数字,且只影响本轮;
- “C” -- 将上一轮有效数字清零,影响有效的上一轮 难点
- 关键在与如何处理好有效数字:
- 有效数字的存储
- 数组
- 栈
- 方法栈
- 有效数字的交替
- 数组存储有效数字,通过下标来对有效数字进行标定
- 栈将有效数字压入、无效数字弹出(题意很符合先入后出的顺序)
- 方法栈通过进入和回退来变换环境,进而调整有效数字
算法实现
利用数组来存储有效数组,下标来标定有效数字位置
class Solution {
public int calPoints(String[] ops) {
// 存储所有有效数字
int[] arr = new int[ops.length+2];
// 第一位有效数字的下标
// 从2开始 可以避免开头第一个字符不是数字
int i = 2;
for (String s : ops) {
// 通过移动下标i来标定最后一位有效数字的位置
switch (s) {
// 前两位有效数字 i-1 i-2
case "+": arr[i] = arr[i-1]+arr[i-2]; i++; break;
case "D": arr[i] = 2*arr[i-1]; i++; break;
// 擦除前一位有效数字 最后一位有效数字位置-1
case "C": arr[i-1] = 0; i--; break;
// 添加一位有效数字 最后一位有效数字位置+1
default:
arr[i] = Integer.valueOf(s);
i++;
}
}
// 将所有有效数字相加求和
int sum = 0;
for (int num : arr) {
sum += num;
}
return sum;
}
}
- 通过数组来存储有效数字,移动下标来操作
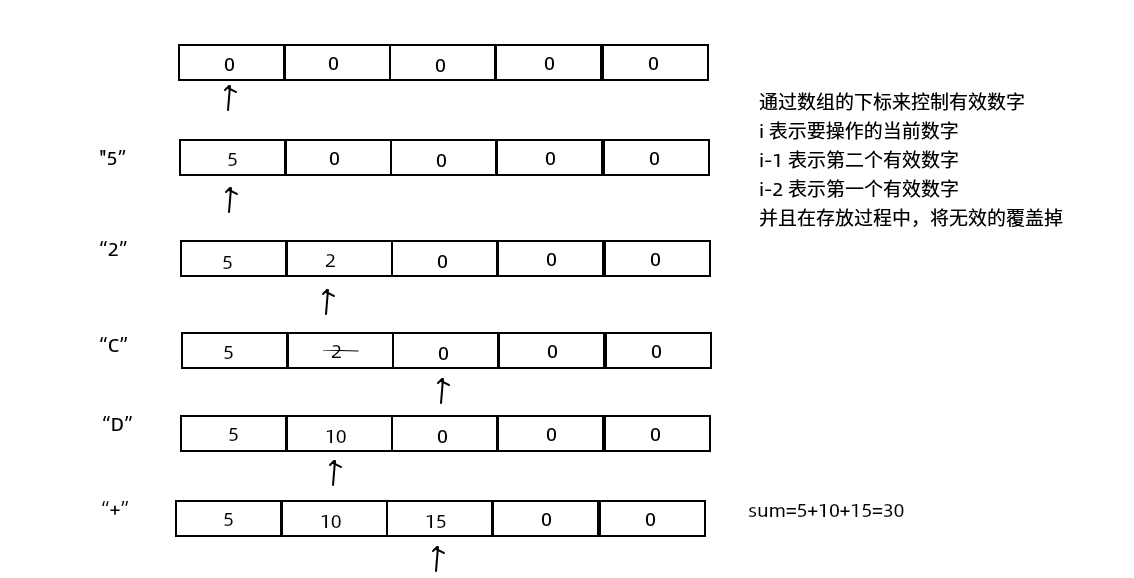
利用栈来存储有效数组,pop()和peek()方法来操作有效数字
class Solution {
public int calPoints(String[] ops) {
// 存储所有有效数字的栈
Stack<Integer> stack = new Stack<>();
for (String s : ops) {
if ("+".equals(s)) {
// 通过peek()可以查看一位有效数字
int top = stack.pop();
int newtop = stack.peek();
// 注意先压入之前弹出的数字
stack.push(top);
stack.push(top+newtop);
} else if ("D".equals(s)) {
stack.push(stack.peek() * 2);
} else if ("C".equals(s)) {
stack.pop();
} else {
stack.push(Integer.parseInt(s));
}
}
int sum = 0;
for (int num : stack) {
sum += num;
}
return sum;
}
}
- 利用栈来存储有效数字,pop()和peek()函数来操作
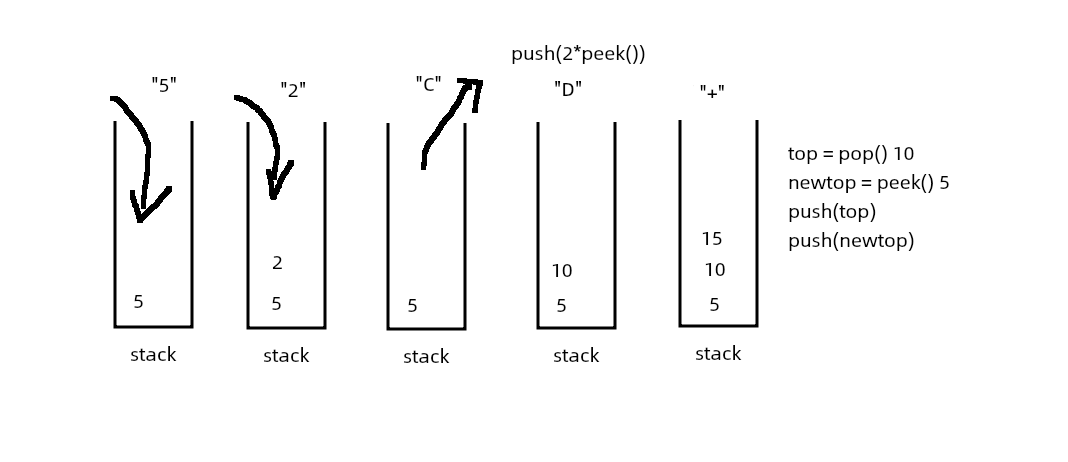
利用递归的方法栈形式,通过回退来切换有效数字
class Solution {
int index = 0, sum = 0;
public int calPoints(String[] ops) {
int len = ops.length;
if (len == 1) {
String element = ops[0];
if (element == "C" || element == "D" || element == "+") return 0;
return Integer.parseInt(element);
}
helper(0, 0, ops);
return sum;
}
/**
* 递归求解
* @param:first 第一位有效数字
* @param:second 第二位有效数字 更靠近当前操作
* @param:ops 存储操作字符的字符串数组
**/
void helper(int first, int second, String[] ops) {
// 通过while循环 解决“C“操作回退后的环境
while (index != ops.length) {
String c = ops[index++];
if ("C".equals(c)) {
sum -= second;
// 此步回退到上一个函数
// 然后进入循环 相当于回退到上两轮的环境
return;
} else if ("D".equals(c)) {
sum += second*2;
helper(second, second*2, ops);
} else if ("+".equals(c)) {
sum += first + second;
helper(second, first+second, ops);
} else {
int num = Integer.parseInt(c);
sum += num;
helper(second, num, ops);
}
}
}
}
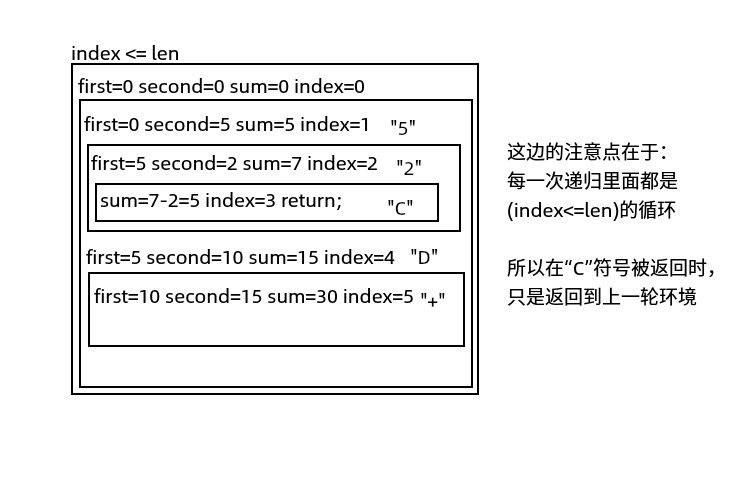
- 通过方法栈实现环境变换
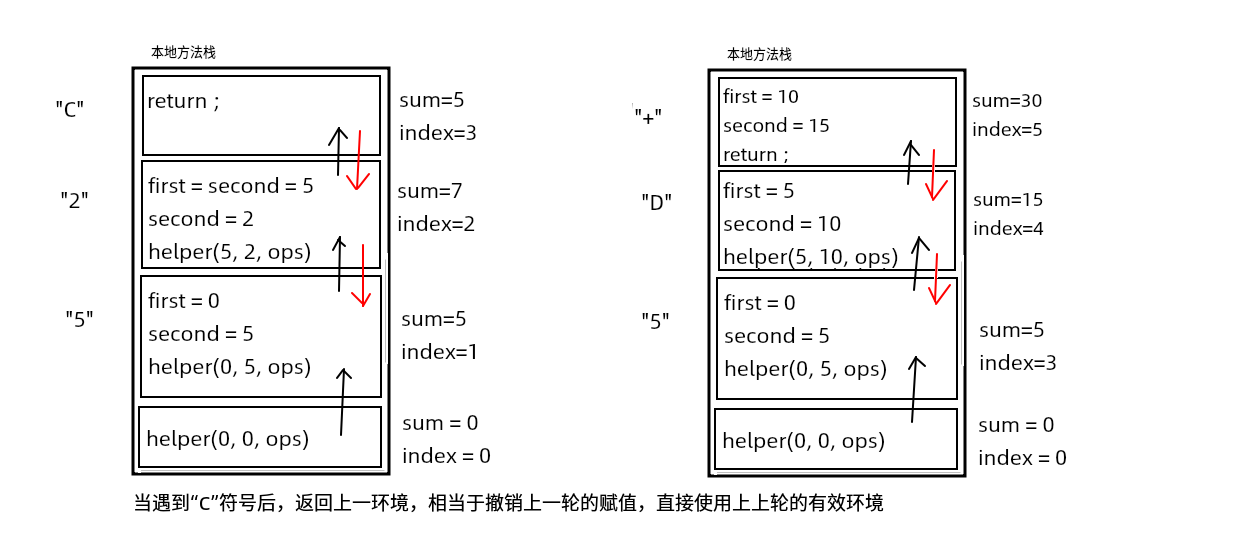
- 以while+递归的角度描述