利用VAR模型科学管理仓位,提升策略效率

更多精彩内容,欢迎关注公众号:数量技术宅,也可添加技术宅个人微信号:sljsz01,与我交流。
VaR模型简述
在我们决定仓位的时候,我们其实需要考虑两个重要变量,一个是可能发生的亏损金额,另一个是发生亏损的可能性。用通俗的语言来打个比方,在99%置信区间下,Var值为2w,那么意味着每次交易亏掉2w权益的可能性是1%。具体公式:
VaR风险度 = 一定置信度下的VaR值/权益 * 100%
VaR模型的计算方法
VaR计算方法很多,比如历史模拟法、蒙特卡洛模拟法、核函数法、半参数法、参数法等。
本次我们使用参数法中的Delta-正太模型:
在服从正态分布的假设下,资产Var值为:
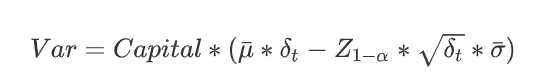
式中,$\bar\mu$是资产期望收益,$\bar\sigma$为标准差,$\delta_t$是要计算的时间长度,$Z{1-\alpha}$是从正太分布表中查到的对应于置信度水平$1-\alpha$的Z值,比如$\alpha = 0.01$的$Z{1-\alpha}=2.326$。
在期货市场中,只要我们把保证金控制在Var最大亏损百分比以上,我们就可以认为在这一置信水平下,可以极大程度防范风险。
通过Var模型评估风险
数据选择
选取近两年的期货所有品种的连续合约价格,置信度的选择,我们选取了99%和95%两个。
核心代码模块
if len(data[price].dropna()) != 0:
#日收益率 收盘价
data['d_return'] = data[price].pct_change()
print(code)
#收益率均值
mean_return = data['d_return'].mean()
#标准差
std = data['d_return'].std()
#VAR值
var1 = mean_return - Z1 * std
var5 = mean_return - Z5 * std
#写入表格
dic = {'code': code,
'var1': var1,
'var5': var5}
if len(table) == 0:
table = pd.DataFrame([dic])
else:
table = table.append([dic])
部分品种VAR结果可视化
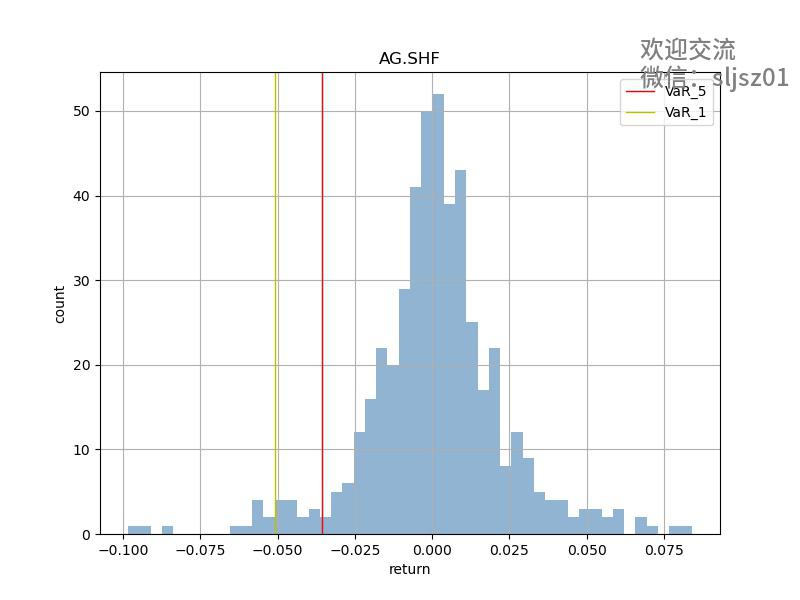
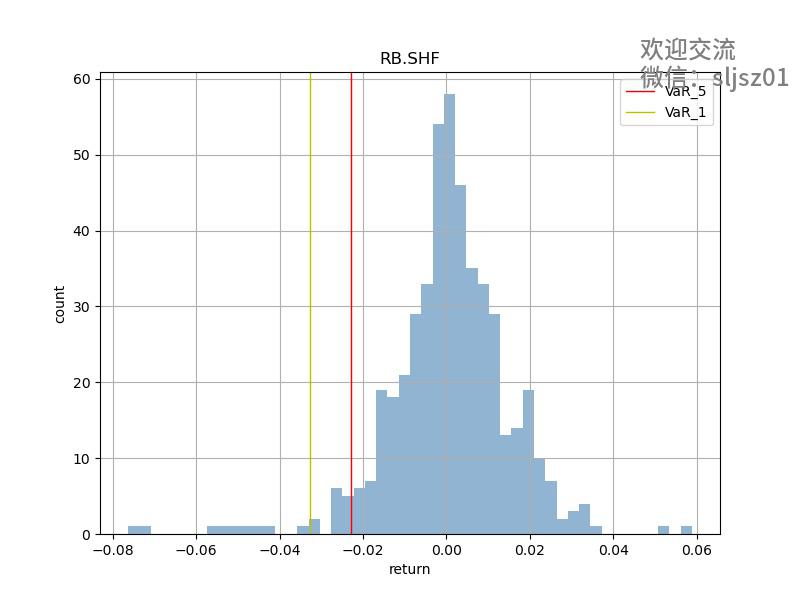


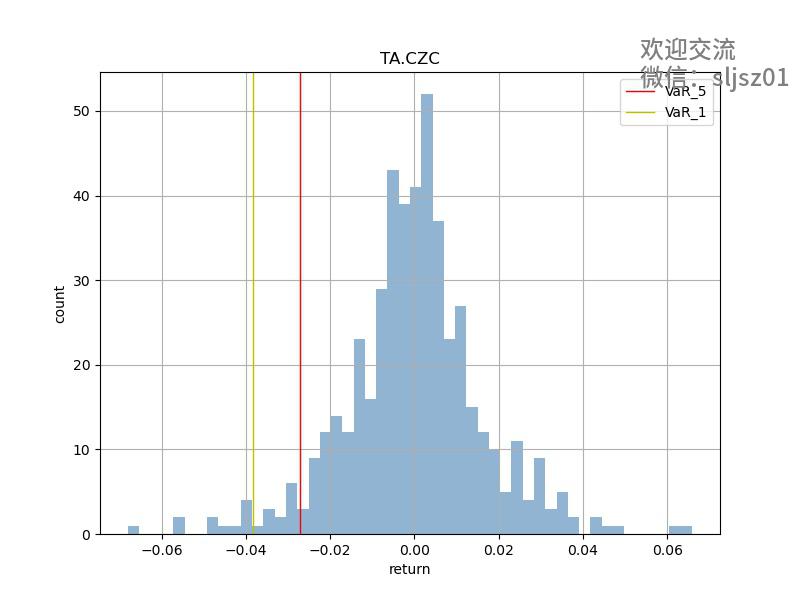
那么我们算出了var之后,仓位的变化是否能够改善投资组合的整体表现呢?
为了排除策略的影响,我们让所有品种都采用最简单的买入并持有策略,在这个策略下,使用所有品种平均持仓和根据var进行仓位微调之后,整个策略的表现是否会有影响。
由于我们使用了var1和var5,因此我们以var1的权重weight_var1,记为w1,同样还有w5,w0表示初始权重,所有仓位平均分配。
我们的目标是计算w0,w1,w5的夏普率的差别,看看通过权重的变化,夏普率是否有所改善。
核心代码模块:
for code in list['wind_code']:
tmp[code] = data[code]*float(table[table['code'] == code]['w1'])
df['w1'] = tmp.sum(axis = 1)
df['w1_return'] = df['w1'].pct_change()
mean1 = df['w1_return'].mean()
std1 = df['w1_return'].std()
sharp1 = 2**0.5*mean1/std1
for code in list['wind_code']:
tmp[code] = data[code]*float(table[table['code'] == code]['w5'])
df['w5'] = tmp.sum(axis = 1)
df['w5_return'] = df['w5'].pct_change()
mean5 = df['w5_return'].mean()
std5 = df['w5_return'].std()
sharp5 = 2**0.5*mean5/std5
最终我们计算得出:
| 均值 | 标准差 | 夏普率 | |
|---|---|---|---|
| 平均仓位 | 0.00064372690041408 | 0.01082542031323569 | 0.08409533179205349 |
| 根据var1调仓 | 0.00078209905493337 | 0.01147973020602057 | 0.09634852655560597 |
| 根据var5调仓 | 0.00078063238309689 | 0.01148086624921166 | 0.09615832807729695 |
可以看到,从夏普率的角度,不论是根据var1调仓还是根据var5调仓,两者数值都有所提高,提高幅度在14.2%。可见,通过VAR模型进行仓位控制,可以在很大程度上,改善投资组合的表现。
VAR仓位管理在量化策略中的表现
我们已经验证了仓位在投资组合当中不可替代的作用,那么在实际的应用表现中,整体仓位比例的变化对于组合的收益率曲线有什么影响。我们以均线策略模型为例,抽取部分策略品种进行体现。从收益率数据的表现看,不管是组合中的品种表现,还是整个组合的表现,var调仓的效果都要比平均仓位的表现要好一些。
部分品种比较曲线,w1代表原始策略表现,w0代表经VAR调整仓位后策略表现:
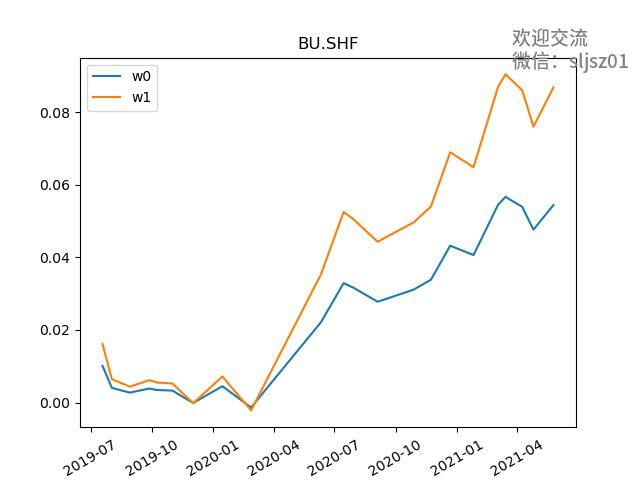

品种汇总曲线,同样的,w1代表原始策略表现,w0代表经VAR调整仓位后策略表现:

想要获取本次分享的完整代码,或是任何关于数据分析、量化投资的问题,欢迎添加技术宅微信:sljsz01,一起交流


往期干货分享推荐阅读
Omega System Trading and Development Club内部分享策略Easylanguage源码
【数量技术宅|量化投资策略系列分享】基于指数移动平均的股指期货交易策略
AMA指标原作者Perry Kaufman 100+套交易策略源码分享
【数量技术宅|金融数据系列分享】套利策略的价差序列计算,恐怕没有你想的那么简单
【数量技术宅|量化投资策略系列分享】成熟交易者期货持仓跟随策略
【数量技术宅|金融数据分析系列分享】为什么中证500(IC)是最适合长期做多的指数
商品现货数据不好拿?商品季节性难跟踪?一键解决没烦恼的Python爬虫分享
【数量技术宅|金融数据分析系列分享】如何正确抄底商品期货、大宗商品





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!