一个真实数据集的完整机器学习解决方案(下)

更多精彩内容,欢迎关注公众号:数量技术宅。想要获取本期分享的完整策略代码,请加技术宅微信:sljsz01
我们先来回顾一下,一个真实数据集的完整机器学习解决方案(上篇)提到,一个完整的机器学习工程的实现步骤:
1. 数据预处理
2. 探索性数据特征统计
3. 特征工程与特征选取
4. 建立基线
5. 机器学习建模
6. 超参数调优
7. 测试集验证
在上篇的内容中,我们介绍了第1到第4步的原理、代码以及实现(可视化)结果,接下来,我们将继续完成这个系列的文章,为大家介绍5-7步的详细原理、流程、代码。
机器学习建模
在进行正式的机器学习建模前,我们还有两项前置工作需要完成。首先,在数据预处理的步骤中,我们剔除了缺失值大于一定比率的数据列,但是在剩下的数据列中,仍然存在着缺失值,对于这一小部分的缺失值,我们将不再丢弃相应的变量列,而是尝试对于缺失值进行填补。
我们读入上一步拆分好的训练数据集以及测试数据集
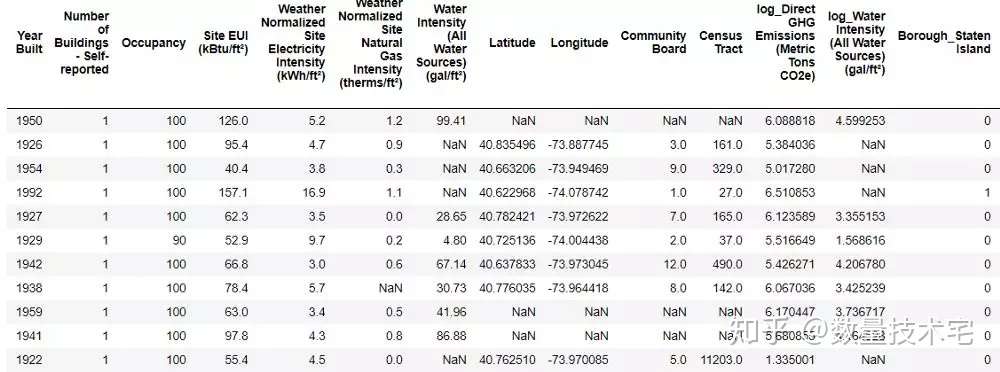
上图中的NaN,都代表着缺失的数据,我们采用一种简单的填补方式,即以每列数据的中位数(Median)作为数值,填充到NaN中。
我们借用Scikit-Learn库中封装好的函数创建了一个以“中位数值替换”(median)为填补策略的Imputer对象。然后,在训练集使用imputer.fit函数计算,用imputer.transform函数填充所有数据(训练集+测试集)中的缺失值。这里需要特别注意的是,测试集中的缺失值也将被相对应训练集中的中值所填充,只有这种填充方式,才能严格的避免测试数据集的数据泄露。这部分的关键实现代码我们也贴在了下图中。

第二项前置工作是数据的归一化,我们知道,真实世界中不同的数据往往有不同的量纲,而且量纲之间差距也很大,如果不做归一化,像支持向量机和K近邻这些会考虑各项特征之间距离的方法,会显著地受到不同特征量纲范围不同的影响。尽管某些模型,比如线性回归、随机森林,对特征量纲不敏感,但考虑到模型的安全性,我们还是建议,所有的建模测试前,都加入这一步骤。
归一化,具体来说,就是对特征的每一个值减去该特征对应的最小值并除以特征值区间(区间=最大值减最小值),我们借用Scikit-Learn中的MinMaxScale函数实现。为避免数据泄露,我们同样只使用训练数据计算区间、最大值和最小值,然后转换所有训练集和测试集的数据。

在做完缺失值填补、特征归一化,这两项前置工作后,接下来我们进入挑选机器学习模型的环节。目前,机器学习的模型日趋多元化,从大量现有的模型中选择最适用当前数据集的模型并不是一件容易的事。
尽管有些“模型分析流图”(以微软制作图为例)尝试指引你选择哪一种模型,但亲自去尝试多种算法,并根据实际的结果判断哪种模型效果最好,也许是更好的选择,机器学习可以说是一个主要由经验而不是理论驱动的领域。
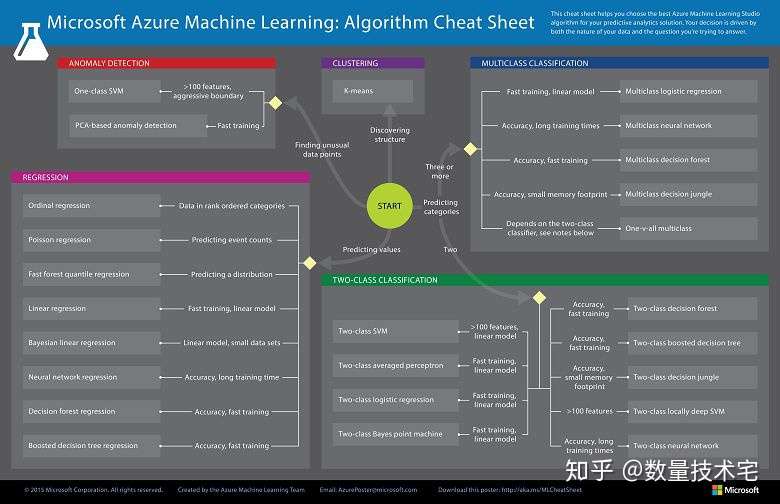
虽然尝试模型的顺序无定式可言,但我们仍然可以遵循由简至繁的基本规律,即从简单的可解释模型(如线性回归)开始尝试,如果发现性能不足再转而使用更复杂但通常更准确的模型。一般来说,模型的可解释性与准确性,是几乎不可同时达到的两极,解释性强,意味着牺牲准确性,相反准确性强,意味着模型复杂化,解释力度变弱。
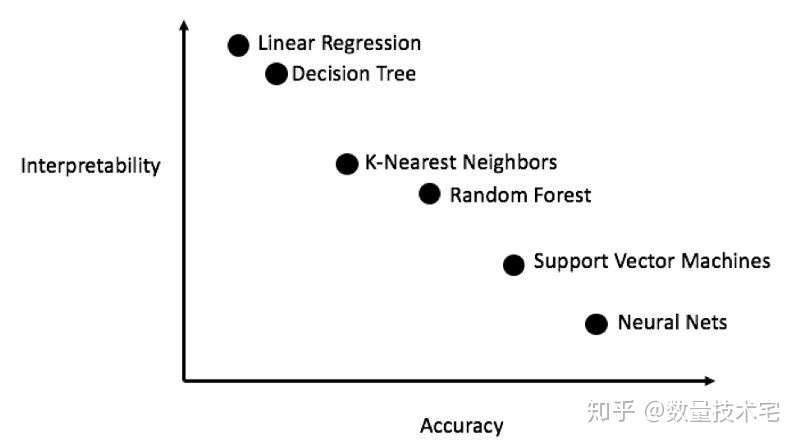
我们在综合考虑解释性、准确性的基础之上,对于本文所涉及的数据集,采用线性回归、K邻近、随机森林、梯度提升、支持向量机这5种主流的机器学习模型,进行逐一的建模和结果比较。
完成所有数据清洗与格式化工作后,接下来的模型创建、训练和预测工作反而相对简单,我们主要通过Scikit-Learn库(以下简称sklearn)完成,sklearn库有详细的帮助文档,对于各种机器学习的算法,大家都可以参考帮助文档相关的方法说明。
我们以梯度提升模型(Gradient Boosting Regressor)为例,为大家展示从创建模型,到训练模型,最后预测模型的这一过程,每个步骤,我们基本都可以借助sklearn库封装好的函数来完成。
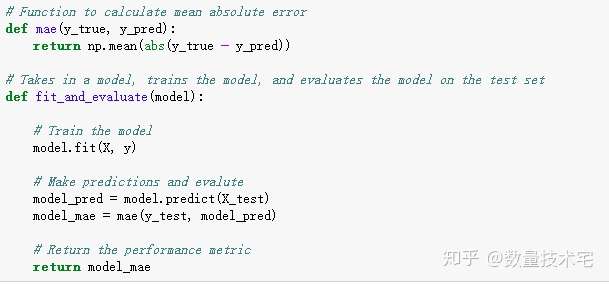

对于其他的模型,我们只需要在构建模型的时候,调用不同的模型对应方法,即可在少量改写代码的前提下,完成所有模型的训练、评估。我们计算得到所有5个模型的Mae指标,并将该指标与基线(Baseline)进行比对。

回顾上文,我们此前计算得到的基线Mae指标的数值为24.5,上述5个模型的Mae都大幅低于基线数值,说明机器学习模型,在这个数据集上,对于最终的目标结果有比较显著的预测能力的改进。
再来对比5个模型相互之间的Mae,可以看到梯度提升模型的Mae最低,而线性回归模型的Mae最高,这也反应了我们此前讲述的逻辑,模型的可解释度(复杂程度)与预测能力是一个反向的关系。
超参数调优
当然,在以上的模型训练中,我们根据经验设置了模型的超参数,并没有对这些参数进行调优处理。对于一个机器学习任务,在确定模型后,我们可以针对我们的任务调整模型超参数,以此来优化模型表现。
在超参数调优工作前,我们先简要介绍一下,超参数与普通参数定义的区别。机器学习中的超参数,通常被认为是数据科学家在训练之前对机器学习算法的设置,常见的有随机森林算法中树的个数或K-近邻算法中设定的邻居数等。
超参数的设定会直接影响模型“欠拟合”与“过拟合”的平衡,进而影响模型表现。欠拟合是指我们的模型不足够复杂(没有足够的自由度)去学习从特征到目标特征的映射。一个欠适合的模型有着很高的偏差(bias),我们可以通过增加模型的复杂度来纠正这种偏差(bias)。而过拟合则相反,它指的是我们的模型过度记忆了训练数据的情况,在样本外的测试集会与训练集有较大的偏差,对于过拟合,我们可以在模型中引入正则化的规则,在一定程度上加以避免。
对于不同的机器学习问题,每个问题都有其特有的最优超参数组合,不存在所有问题通用的最优解。因此,超参数的遍历、寻优,是找到最优超参数组合的唯一有效方式。我们同样借用sklearn库中的相关函数完成超参数的寻优,并通过随机搜索(Random Search)、交叉验证(Cross Validation)这两种方法实现。
随机搜索(Random Search)是指,定义一个网格后采用随机抽样的方式,选取不同的超参数组合,随机搜索相比较普通的全网格搜索,在不影响优化性能的前提下,大幅减少了参数寻优的时间。
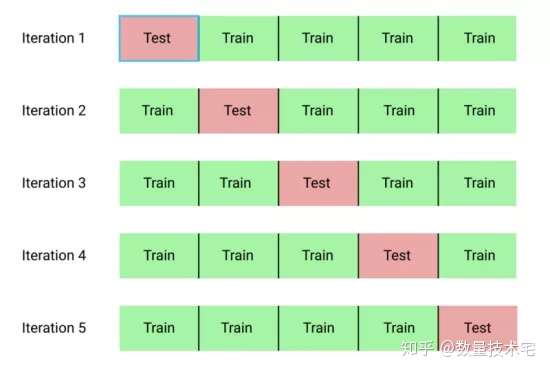
交叉验证(Cross Validation),又称为K折交叉验证,原始样本被随机划分为k等份子样本。在k份子样本中,依次保留一个子样本作为测试模型的验证集,剩下的k-1子样本用作模型训练,重复进行k次(the folds)交叉验证过程,每一个子样本都作为验证数据被使用一次。然后,这些折叠的k结果可以被平均(或其他组合)产生一个单一的估计。最后,我们将K次迭代的平均误差作为最终的性能指标。
我们还是以前文中举例的梯度提升回归模型(Gradient Boosted Regressor)为例,来演示随机搜索与交叉验证的过程。梯度提升回归模型(有多项超参数,具体可以查看sklearn库的官方文档以了解详细信息。我们对以下的超参数组合进行调优:
- loss:损失函数的最小值设定
- n_estimators:所使用的弱“学习者”(决策树)的数量
- max_depth:决策树的最大深度
- min_samples_leaf:决策树的叶节点所需的最小示例个数
- min_samples_split:分割决策树节点所需的最小示例个数
- max_features:最多用于分割节点的特征个数
首先确定各个超参数的遍历范围取值,以构建一个超参数寻优网络,对于梯度提升回归模型,我们选择如下的超参数寻优网络

紧接着,我们创建一个RandomizedSearchCV对象,通过sklearn库中的内置函数,采用4折交叉验证(cv=4),执行超参数寻优。

在完成超参数寻优的计算过程后,best_estimater方法将展示刚才寻优过程中找到的最佳超参数组合。
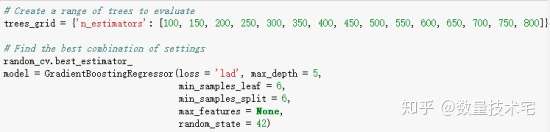
理论上,我们可以进行无限多次的超参数寻优,不断调整超参数的范围以找到最优解,但技术宅不建议大家过度去执行这个步骤,对于一个机器学习模型来说,优秀的特征工程,其重要性要远大于广泛的超参数寻优遍历。机器学习的收益递减规律是指,特征工程能对模型有较大提升,而超参调整则只能起到锦上添花的效果。
对于单一参数的调整寻优,我们也可以通过图形可视化的方式进行观察,比如下图我们仅改变决策树的数量,来观察模型的表现变化情况。
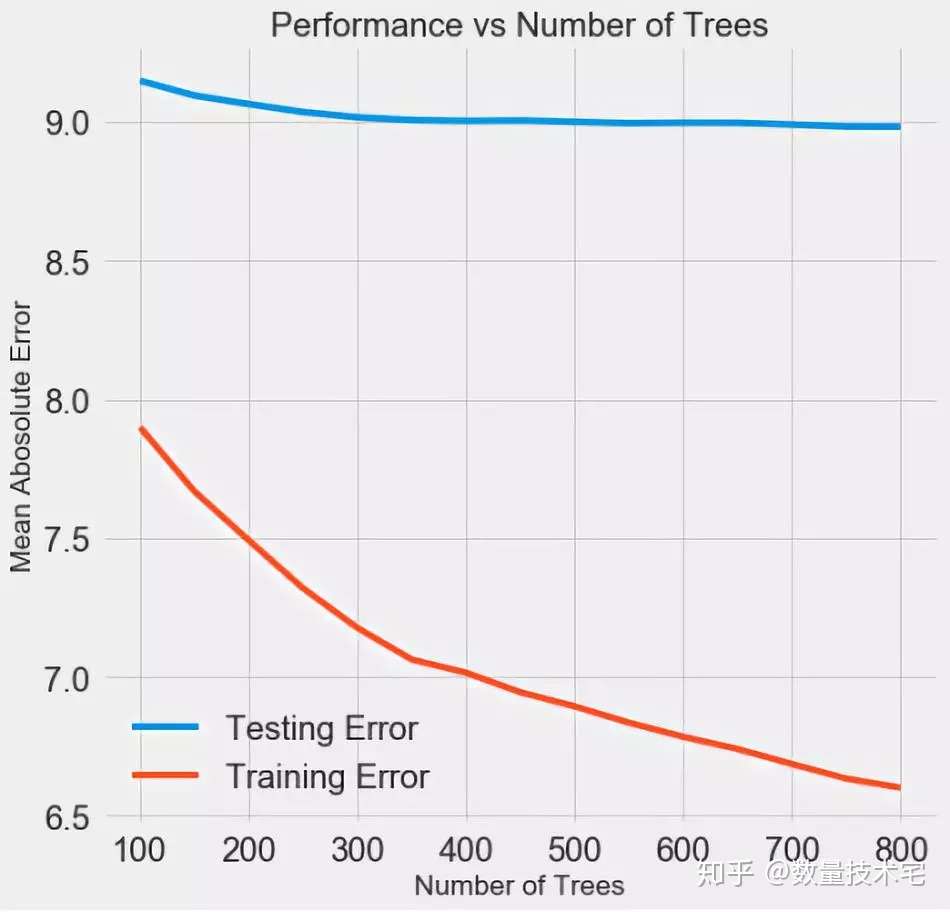
随着模型使用的树的个数增加,训练集误差和测试集误差都会减少。但我们需要看到虽然训练集的误差一直在减少,但测试集的误差,在树的数量到达300-400后,几乎不下降了。这就说明过度增加决策树的个数,最终带来的只是在训练集上的过度拟合,而对测试集没有什么增量的帮助。
针对这种情况,一方面我们可以增加样本的数量,获取更多的数据用于训练、测试,另一方面,我们也可以适当降低模型的复杂度。
测试集验证
在此前所有的数据处理和建模的步骤中,我们都需要杜绝数据泄露的情况发生,只有这样,我们才能在测试集上准确、客观地评估模型的最终性能。
我们对比超参数寻优前、寻优后,两个模型在测试集上的表现,并以Mae作为评估指标。
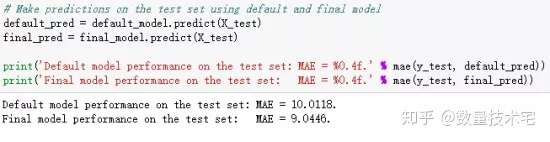
可以看到,经过超参数寻优后确定的模型,相比较未寻优的模型,Mae降低了约10%,也就是说模型的预测精度上升了10%,这个改善幅度,对于超参数寻优来说,已经是一个不错的幅度了。
但对于这个寻优的过程来说,是需要花费一定的时间成本的,例如我们的这个寻优,相比原始的模型,花费了原始模型约10倍左右的时间,从1s不到到12s。这也说明了机器学习是一种“权衡游戏”,我们需要不断地平衡准确性与可解释性、偏差与方差、准确性与运行时间等表现。正确的组合是因问题而异的。


现在,我们已经有了最终超参调优后的模型,就可以使用该模型,来评估他们与真实值的偏差了,我们对于测试集,绘制预测值与实际值的密度图对比,以及预测值减去实际值所得到的残差hist图,来对模型的预测效果进行可视化的展示。
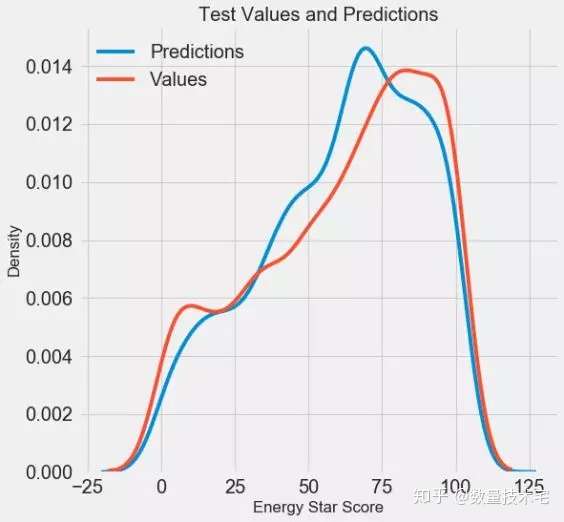
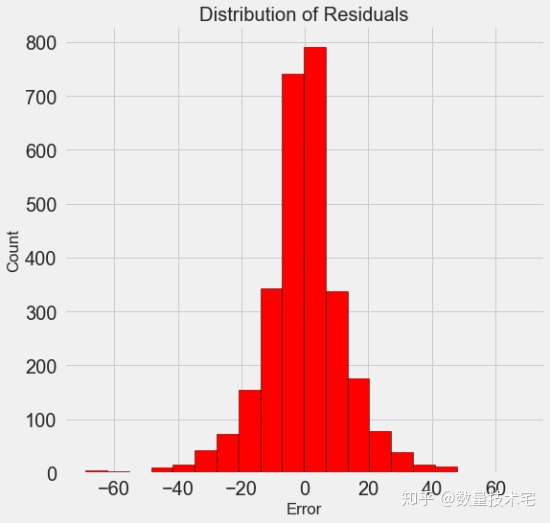
我们来分析一下这个可视化的结果:虽然模型预测值的密度峰值接近中值在66附近,而非真实值的100左右密度峰值,但模型预测值密度分布大致接近实际值密度分布。而模型预测值与真实值的残差分布,也是符合正态分布的。
最后,这个结果说明了,我们构建的梯度提升回归机器学习模型,能够较为准确的预测样本外的建筑物能源之星得分,达到了我们最初预测目标变量的这一实际目的。
那么,我们这个系列的文章(上篇、下篇)到这里全部结束了,感谢耐心读完长文的粉丝,技术宅真诚的希望,通过自己的文字,让你有所收获有所得。
关注 “数量技术宅”不迷路,您的点赞、转发,是我输出干货,最大的动力


往期干货分享推荐阅读
【数量技术宅|量化投资策略系列分享】基于指数移动平均的股指期货交易策略
AMA指标原作者Perry Kaufman 100+套交易策略源码分享
【数量技术宅|金融数据系列分享】套利策略的价差序列计算,恐怕没有你想的那么简单
【数量技术宅|量化投资策略系列分享】成熟交易者期货持仓跟随策略
【数量技术宅|金融数据分析系列分享】为什么中证500(IC)是最适合长期做多的指数
商品现货数据不好拿?商品季节性难跟踪?一键解决没烦恼的Python爬虫分享
【数量技术宅|金融数据分析系列分享】如何正确抄底商品期货、大宗商品


 浙公网安备 33010602011771号
浙公网安备 33010602011771号