树状数组学习小记
初看树状数组的概念以及定义,还料想不算太复杂,不愧是线段树的的阉割版本,用起来省时省事,复杂度还底。简直称得上要多爽就又多爽呀。
树状数组一般适用于三类问题:
1,修改一个点求一个区间
2,修改一个区间求一个点
3,求逆序列对
要介绍树状数组,先po上他最直观的图,便于理解。
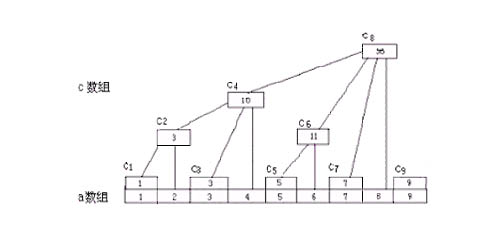
不难看出以下规律:
c1=a1
c2=a1+a2
c3=a3
c4=a1+a2+a3+a4
c5=a5
c6=a5+a6
c7=a7
c8=a1+a2+a3+a4+a5+a6+a7+a8
c9=a9
c10=a9+a10
c11=a11........
c16=a1+a2+a3+a4+a5+.......+a16。
可以归纳出通项:
cn=a(n-2^k+1)+.........+an,Cn由多少项取决于他最多能够整除2的几次方。比如6最多能整除2的1次方,所以C6就有数组a的两项组成。而奇数都最能整除2的0次方,所以当n为奇数时,由Cn = An。
也正是因为这些性质,使得树状数组可以在当原数组的某些项(一般是一个区间)的值变化的时候,可以快速求出区间和。这个在数据量特别大的时候尤为有用,有效解决各种超时。所以说,树状数组只要用于区间值求和或区间修改求值,复杂度为O(lgn),这在n特别大时,比O(n)低了一个数量级。
由Cn的公式我们不难看出,要想求Cn就必须要求出2^k的k值。这个很容易让我们想到二进制,而实际上他可以由 x & (x ^ (x - 1))求出。
这个公式不难理解,不过在大部分程序中,都是用x & (-x)来实现。一开始我十分不解,演算了半天也找不出这两者的关系。后来发现,这是利用计算机补码的性质(囧rz,真该好好补补我的计算机原理方面的知识了)。
在代码中,我们一般这样写:
1 int lowbit(int x) 2 { 3 return x&(-x); 4 }
看着上面的图,从1到n的求和代码也不难想
int Sum(int n) { int sum=0; while(n>0) { sum+=c[n]; n=n-lowbit(n); } return sum; }
以上就是树状数组就根本的操作,而在实际应用中的变化也都由上面的推出来的。
不过,在真正的应用中,总体而言,还是包含有三种用法。
(1)最为简单的,改点求段。
树状数组的定义来看,修改一个点ai,对且仅对cn(n >= i)由影响。所以我们只需要逐次修改后面的cn即可。
代码如下:
1 void update(int i, int c) { 2 while(i <= n) { 3 num[i] += c; 4 i += lowbit(i); 5 } 6 }
而对于段的求和,我们可以直接调用上面的Sum函数,由于Sum时计算从1到i的,而当我们需要计算x到y区间的和的时候,就调用Sum(y) - Sum(x -1).即可
(2)其次,就是改段求点。
(3)改段求段。 挖坑待填:P






