首先当然是我们最简单的冒泡排序了
冒泡排序的原理很简单,就是逐步比较相邻两个元素的大小,最多比较N-1次就能够将序列排好序了
缺点也同样很明显,时间复杂度很高O(n^2),可以做出的优化方案就是,如果在一次冒泡的过程中没有发生值的比较,那么这个序列就已经是有序的了

文中图源于菜鸟教程
1 def maopao(l): 2 for i in range(len(l) - 1): 3 flag = True 4 for j in range(len(l) - i - 1): 5 if l[j] > l[j+1]: # 大于就是升序,小于就是降序 6 l[j], l[j+1] = l[j+1], l[j] 7 flag = False 8 if flag: 9 break 10 return l 11 12 13 l = [3,2,5,6,7,8,1,4,0] 14 s = maopao(l) 15 print(s)
不要在意我的变量命名~
其次是插入排序,插入排序也很简单,一句话总结就是在一个有序序列中插入数据。

有图之后写代码实在是太直观了
1 def insert_sort(l): 2 for i in range(1, len(l)): 3 j = i-1 4 while l[j] > l[i]: 5 l[j], l[i] = l[i], l[j] 6 if j > 0: 7 i = i-1 8 j = j-1 9 return l 10 11 12 l = [10,3,2,5,6,7,8,1,4,0,-1] 13 s = insert_sort(l) 14 print(s)
很容易就发现插入排序的时间复杂度也是O(N^2),那么有没有什么优化方案呢?那当然是有的,那就是接下来要介绍的折半插入排序和希尔排序。
首先是折半插入排序,折半插入排序也经常用于在有序序列中插入一个数据使得序列依旧保持有序。
那什么是折半插入排序呢?从名字就能够看出来一部分,简单来说就是先将序列的一部分排序,然后将下一个待排序数据以二分查找的方式找到应该插入的位置。比如python中使用的著名的timsort排序算法就是结合了归并排序和插入排序的一种高效的排序算法。timsort算法比较复杂,感兴趣的可以自行去源码中看一下~,文中不做介绍。
折半插入排序说到底还是一个二分查找算法的应用,因此我们首先需要了解的是二分查找。
二分查找就是每次查找都将查找的范围缩小一半,第一次我们就比较待插入数据与序列中间的数,如果比中间的数大,就将待插入数据与右半序列比较,以此类推,直到找到可以插入的位置为止。
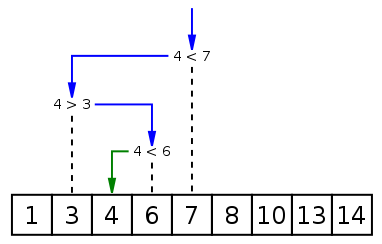
上图所示就是将4插入到原有序序列的一个过程演示。
1 def binary_search(l, n, min, max): 2 p = (min + max) // 2 3 if min > max: 4 return min 5 elif min == max: 6 if n > l[min]: 7 return min + 1 8 elif n < l[min] and n: 9 return min 10 else: 11 return 0 12 elif n > l[p]: 13 return binary_search(l, n, p + 1, max) 14 elif n < l[p]: 15 return binary_search(l, n, min, p - 1) 16 elif n == l[p]: 17 return p 18 19 20 def binary_sort(l): 21 for i in range(1, len(l)): 22 p = binary_search(l[:i], l[i], 0, i-1) 23 l.insert(p, l.pop(i)) 24 print(l) 25 return l 26 27 28 l = [2, 10, 1, 6, 0, 8, 7, 100, 30, -5, 4] 29 s = binary_sort(l) 30 print(s)
二分插入我是用递归写的,递归的两大要素,第一,每次使用递归都可以减少问题的规模,第二,明确终止条件。
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率比直接插入排序有较大提高。
接下来就是希尔排序了,定义我就不多解释了,上面这段话说的非常棒。
1 def insert_sort(l): 2 for i in range(1, len(l)): 3 j = i-1 4 while l[j] > l[i]: 5 l[j], l[i] = l[i], l[j] 6 if j > 0: 7 i = i-1 8 j = j-1 9 return l 10 11 12 def shell_sort(l): 13 increment = len(l) // 2 14 while increment > 0: 15 for i in range(increment): 16 t = insert_sort(l[i::increment]) 17 l[i::increment] = t 18 increment //= 2 19 return l 20 21 22 l = [100, 2, 10, 1, 6, 0, 8, 7, 100, 30, -5, 4] 23 s = shell_sort(l) 24 print(s)
就顺带使用上面的插入排序的代码了~
希尔排序是不稳定的排序,不是指结果可能会无序,而是指它的时间复杂度,O(nlog(n))~O(n*n),原因就在于如果待排序序列中有相同元素存在就会导致相同的元素在不同的插入排序中频繁调整位置。


