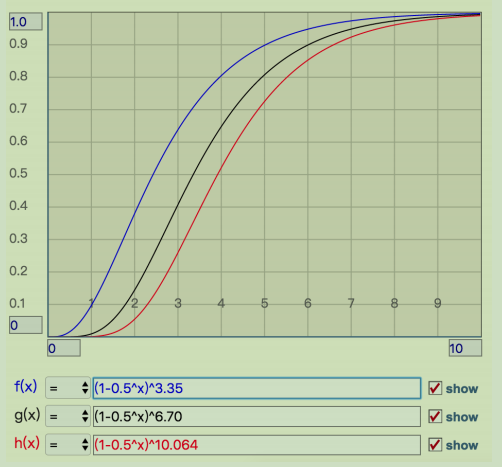
应用场景:比如我们在某站看视频的时候,每次我们加载刷新之后看到的都是之前没看过的新闻,这个时候需要用什么结构来实现呢?
第一反应可以使用一个set,每次加载的时候就用exists判断一下,这种方式问题也是很明显的,在高并发量或者set很大的时候会严重拖垮数据库。作者还举例了使用缓存,但是缓存也同样面临着消耗的存储空间会逐渐达到一个难以接受的地步。这个时候布隆过滤器就闪亮登场了,它就是专门用于解决这类缓存问题的,并且能够节省90%以上的空间。
什么是布隆过滤器?
布隆过滤器可以理解为一个不太准确的set,可以使用它的contains方法来判断一个元素是否存在。但是它也不是那么不准确,参数设计合理的前提下,它的误差完全可以接受。值得注意的是,如果布隆过滤器告诉你一个元素存在,那么可能这个元素不存在;如果布隆过滤器告诉你一个元素不存在,那么这个元素肯定不存在。应用到上面所说的场景中就可能会导致一部分我没看过的新闻也没推送给我,但是我看过的新闻就一定不会推送给我。
相关指令:
bf.add
bf.exists
bf.madd
bf.mexists
指令很简单,我就不多做解释了。
通过add指令创建的布隆过滤器使用的是默认参数,在实际使用的过程中准确率可能会不高,redis还提供了一种手动创建布隆过滤器的方式:
bf.reserve key error_rate initial_size
error_rate是错误率,错误率越低需要的空间越大;initial_size是预计将要存储的数据量,如果实际存储的时候超过了这个数据量,错误率也会变大。默认的error_rate是0.01,initial_size是100。在设置initial_size时需要尽量接近实际需要,太大浪费空间,太小错误率会影响错误率,还需要留出一定的冗余空间。
布隆过滤器的原理还是比较容易猜到的,就是之前文中说到的redis的应用之一,位图,一个大型的位图数组加上一个合适的hash算法就是布隆过滤器了。布隆过滤器使用的hash算法是无偏hash算法,即能够把元素的hash值算的比较均匀。向布隆过滤器中添加值时会使用几个hash函数对key进行hash计算出一个值,再对数组长度取模,将几个hash函数的结果都设置为1就完成了add操作。判断是否存在的时候原理也是一样的,求出hash值,取模,只要取模的结果中任意一位为1,那么就认为这个key存在。
使用布隆过滤器的时候需要注意,不要使存储的数据远大于initial_size,如果已经超出了,那么则要对布隆过滤器进行重建,将之前的数据再一次add到新的布隆过滤器中(要求在其他地方存储下这些数据)
关于布隆过滤器的空间占用:
关于空间占用有两个简单的公式,但是推导过程很复杂。。。那我不看了,
它的空间占用和两个值有关,很显然就是error_rate(f)和initial_size(n)了,根据推导公式可以根据这两个输入得到两个输出分别是位数组的长度l,hash函数的最佳数量k。公式如下: