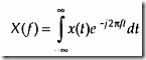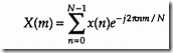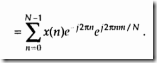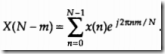Discreat fourier transform summary

Discreat fourier transform  summary

1. 傅里叶变换 与 离散傅里叶变换DFT

DFT 是一个数学过程：用于确定离散信号的频率成分。

离散信号时重连续信号中采样而得。

来看下数学语言表达：

傅里叶变换：

DFT:

2. 对于DFT的理解：

先来一段直觉上的理解：（是傅里叶变换的理解）（来句题外话：数学语言果然是最简洁精确的科学语言！！！！）

傅里叶变化是将时域的信息转到频域，重而可以重另一个角度来处理这些在时域上比较复杂的信息

这是一个时域到频域的映射过程

在频域中是由这些个‘频域分量’构成频域世界的坐标（其实本来是频率本身作为坐标的）。 我认为cos与sin只是作为频率的载体

（sin与cos函数中同时存在时间与频率cos（wt））频率与时间无法直接映射所以只能找cos这个函数作为中转站

假设时间域必可转换成频域

频域基本元素f       （某种联系）基本元素cos（wt）        由假设得 时域中任何信号必可用的集合表示

我们需要的是一个时间与频率的关系 这样当我们在对频率信号处理时 即是对时间信号处理

当f与cos（wt）联系上时 （cos是整个时间域上的函数）  f已经与整个时间域上所有t有啦联系

而我们需要把时间域上的幅值映射到频域   这里用到的一个方法是把某个频率的cos函数与每个时域t上的幅值相乘 ，最后相加 ，代表这个频率的幅值

至此，t与f的映射已经很明了啦

最后强调;我们只需要一种关系一种映射 我们可以变来变去 选择任何一个容易处理的状态，处理好后变成另一个我们需要的状态   只要我们清楚他们之间的关系！！！

先用欧拉公式对原式展开：

对以上各种字母的理解：

注意：ω=(2πm)/N

：为第m个DFT的输出 

为各个输入采样点的序列（值）

N :为输入序列的样点数 同时也表示经过DFT后 输出的频率点数

因此可产生的频率数为N个。   因为是离散的所以频率成分有限

（时域上输入N个采样点，在DFT后频域上会输出N个值）

（N决定频域输出结果的分辨率（即最小频率间隔） 以及计算N点DFT的处理时间）

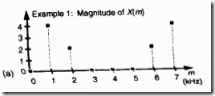
来看看这个式子吧哪些信息联系起来啦：

其中有相位与和幅值两个信息

简单的表示为

幅值信息：

相位：

提一下：幅度的平方为功率谱

强调：1.单个X(m)的输出是项与项的乘积之和，是输入采样序列与频率为m/N的正弦波的相关

2.当DFT 的输入采样值为实数时，DFT输出项是对称的。

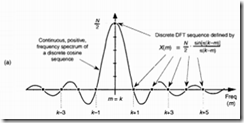
来看下DFT 的对称性

当输入序列为实数时     m>N/2时频域上幅度的输出值与前半部分相同  且实部偶对称 虚部奇对称

数学解释：

DFT的线性：

两个信号的DFT等于各个信号的和

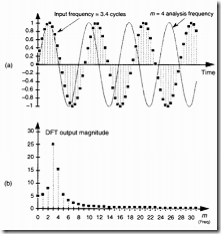
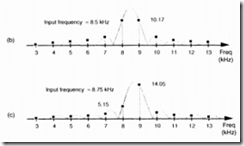
DFT泄漏

个点与相对应的分析频率

当输入信号的频率成分不是精确等于分析频率是就会发生频率泄漏

DFT输出为曲线上的离散点

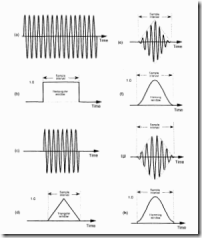
窗

加窗为了使旁瓣幅度减小 从而减小泄漏

距形窗 三角窗 汗宁窗

.当旁瓣幅值减小, 同时DFT频率分辨率减小

DFT 分辨率 补零 频域采样

小结

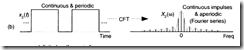
连续傅里叶变换continuous fourier transform

傅里叶级数 fourier series

离散时间傅里叶变换discrete-time fourier trandform

离散傅里叶变换discrete fourier trandform