组合逻辑与时序逻辑，逻辑的接口处数据稳定处理摘记

1.1 建立时间与保持时间

建立时间（Tsu：set up time）是指在时钟沿到来之前数据从不稳定到稳定所需的时间，如果建立的时间不满足要求那么数据将不能在这个时钟上升沿被稳定的打入触发器；

     保持时间（Th：hold time）是指数据稳定后保持的时间，如果保持时间不满足要求那么数据同样也不能被稳定的打入触发器。建立与保持时间的简单示意图如下图1所示。

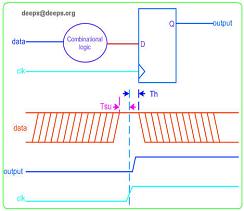
图1 保持时间与建立时间的示意图

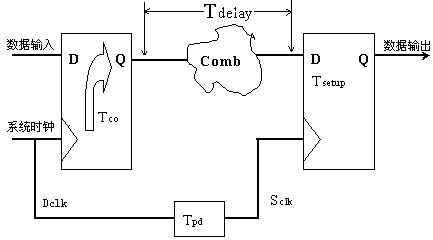
图2 同步设计中的一个基本模型

图2为统一采用一个时钟的同步设计中一个基本的模型。图中

Tco：是触发器的数据输出的延时；

Tdelay：是组合逻辑的延时；

Tsetup：是触发器的建立时间；

Tpd：为时钟的延时（可以忽略不计）。

T：为时钟周期

T3：D2建立时间

T4：D2保持时间

     如果第一个触发器D1建立时间最大为T1max，最小为T1min，组合逻辑的延时最大为T2max，最小为T2min。问第二个触发器D2建立时间T3与保持时间T4应该满足什么条件，或者是知道了T3与T4那么能容许的最大时钟周期是多少。这个问题是在设计中必须考虑的问题，只有弄清了这个问题才能保证所设计的组合逻辑的延时是否满足了要求。

//**************************************************************************************************************************************

我的想法：理想情况每个时钟上升沿DFF1与DFF2的数据都要跟新，但存在TCO,与Tdelay，当T<TCO+Tdelay也就是说时钟周期太短DFF1的Q1还没传到DFF2的D2，不符合我们的实际设计想法
DFF2还需建立时间T3，有应为在T4内收到CLK 上升沿数据读取才稳定 所以 T>T3+Tdelay+TCO   ；（T4在CLK上升沿前的一段就是上式大于的余量）；

//**************************************************************************************************************************************

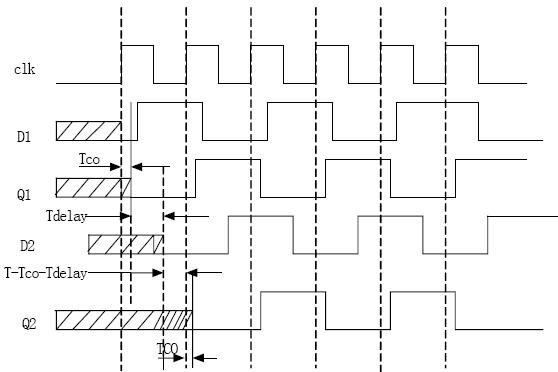
图3 符合要求的时序图

从上面的时序图中也可以看出，D2的建立时间与保持时间与D1的建立与保持时间是没有关系的（CLK上升沿只有出现在在保持时间开始之后才能稳定读取，一旦上升沿之后则立即进入TCO，不存在剩余的DFF1的保持时间），而只和D2前面的组合逻辑和D1的数据传输延时有关，（CLK周期确定其他延时占的时间多拉，Thold就短啦）

延时没有叠加效应:每个CLK周期内的延迟相互独立，不会叠加；

时钟出现较大的延时多是采用了异步时钟的设计方法，这种方法较难保证数据的同步性，所以实际的设计中很少采用。

当时钟存在延时:

 

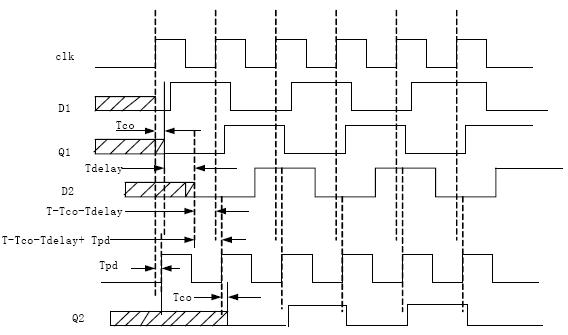
Tpd＋T-Tco-T2max>T3

1.2如何减小合逻辑的延时

1.2.1 通过改变走线的方式来减小延时

以altera的器件为例，我们在quartus里面的timing closure floorplan可以看到有很多条条块块，我们可以将条条块块按行和按列分，每一个条块代表1个LAB，每个LAB里有8个或者是10个LE。它们的走线时延的关系如下：同一个LAB中（最快） < 同列或者同行 < 不同行且不同列。我们通过给综合器加适当的约束（约束要适量，一般以加5%裕量较为合适，比如电路工作在100Mhz，则加约束加到105Mhz就可以了，过大的约束效果反而不好，且极大增加综合时间）可以将相关的逻辑在布线时尽量布的靠近一点，从而减少走线的时延。

1.2.2 通过拆分组合逻辑的方法来减小延时(流水线)

由于一般同步电路都不止一级锁存（如图8），而要使电路稳定工作，时钟周期必须满足最大延时要求，缩短最长延时路径，才可提高电路的工作频率。如图7所示：我们可以将较大的组合逻辑分解为较小的几块，中间插入触发器，这样可以提高电路的工作频率。这也是所谓“流水线”（pipelining）技术的基本原理。

对于图8的上半部分，它时钟频率受制于第二个较大的组合逻辑的延时，通过适当的方法平均分配组合逻辑，可以避免在两个触发器之间出现过大的延时，消除速度瓶颈。

图7 分割组合逻辑

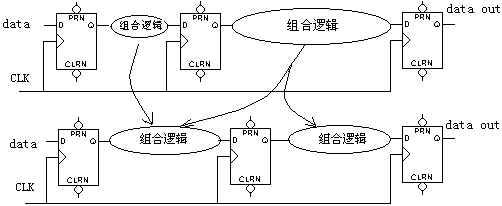
图8 转移组合逻辑