区间合并

区间合并的朴素做法

• 时间复杂度O(n2)
• 第一层循环遍历遍历区间,然后第二层循环去查找区间看能否合并然后更新,时间复杂度太高了

区间合并的贪心做法

• 时间复杂度O(nlogn)
• 步骤：

1. 左端点为关键字然后从小到大排序
2. 当前区间和下一个区间的关系有三种：
   
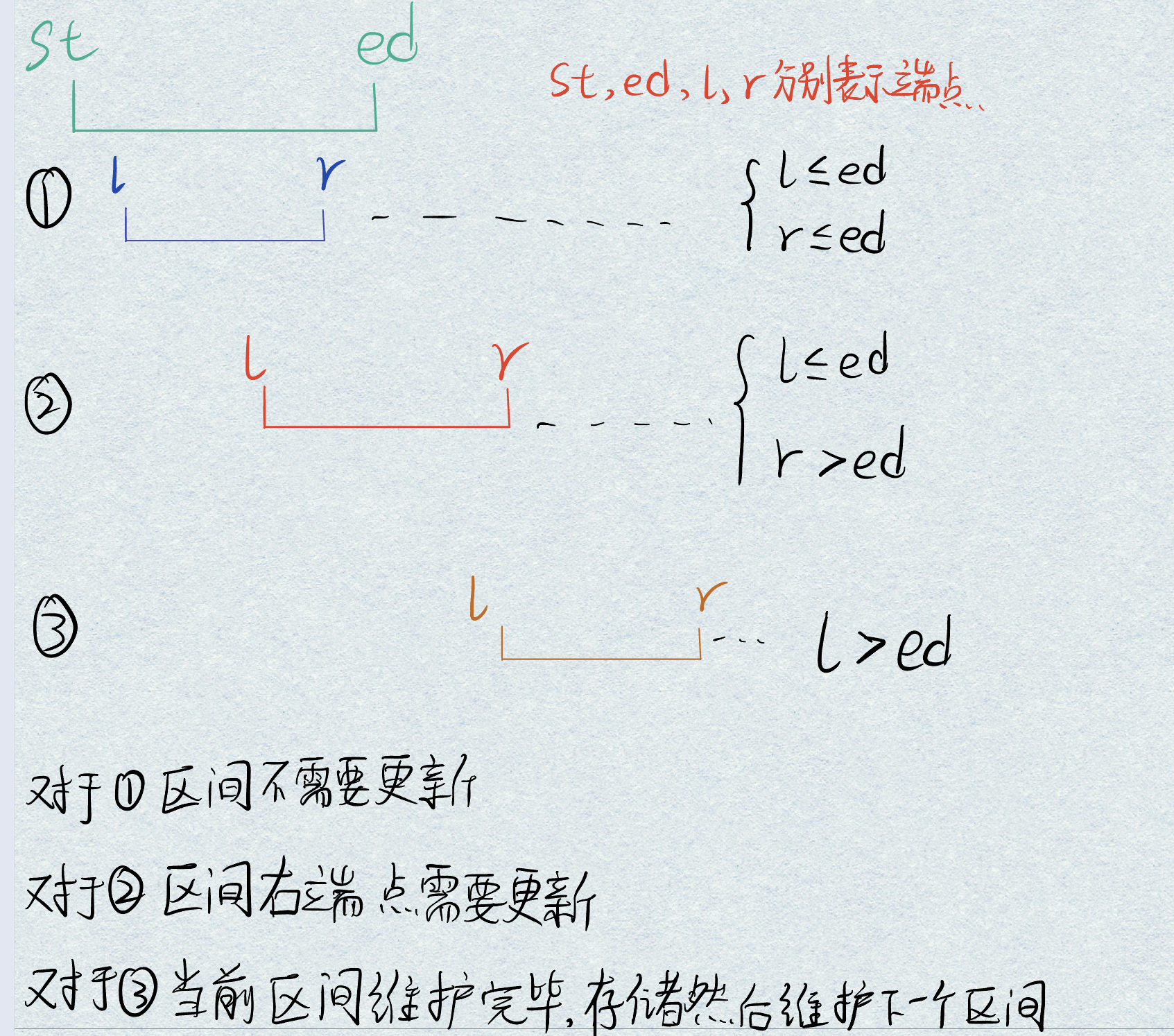
3. 核心板子代码

// 将所有存在交集的区间合并
inline vector<PII> merge(vector<PII>& ref) {
    sort(ref.begin(), ref.end());              //pair默认按第一个参数排序
    int st = -INF, ed = -INF;
    vector<PII> res;
    for (int i = 0; i < ref.size(); ++i) {
        if (ed < ref[i].first) {
            if (ed != -INF)res.push_back({ st,ed });   //如果不是一开始的区间就加进去
            st = ref[i].first, ed = ref[i].second;      //更新区间
        }
        ed = max(ref[i].second, ed);                //合并区间,右端点取最大值
    }
    if (st != INF) res.push_back({ st, ed });  //记得把最后一次操作的区间加进去,为什么得st != INF呢？防止集合为空
    return res;
}

4. 板子题链接: https://www.acwing.com/problem/content/805/
5. 板子题代码:

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> PII;
int arr[N];
vector<PII> vec;
inline int max(const int& a, const int& b) {
    return a > b ? a : b;
}

//区间合并板子
inline vector<PII> merge(vector<PII>& ref) {
    sort(ref.begin(), ref.end());              //pair默认按第一个参数排序
    int st = -INF, ed = -INF;
    vector<PII> res;
    for (int i = 0; i < ref.size(); ++i) {
        if (ed < ref[i].first) {
            if (ed != -INF)res.push_back({ st,ed });   //如果不是一开始的区间就加进去
            st = ref[i].first, ed = ref[i].second;      //更新区间
        }
        ed = max(ref[i].second, ed);                //合并区间,右端点取最大值
    }
    if (st != INF) res.push_back({ st, ed });  //记得把最后一次操作的区间加进去,为什么得st != INF呢？防止集合为空时，把两个st = INF， ed = INF存入结果中
    return res;
}


int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        int l, r;
        cin >> l >> r;
        vec.push_back({ l,r });
    }
    auto res = merge(vec);

    cout << res.size() << endl;
    
    return 0;
}

补充

• 跟区间有关的问题很多都是用贪心,先左端点或者右端点排序，或者双关键字排序