哈希表

参考:

哈希表：

  • 哈希表就是通过哈希函数把x映射成唯一对应的y，y作为key，x作为value通过y可以索引x，其实数组就是一个哈希表，但这个通过哈希函数生成的key可能会发生哈希
    通过key可以迅速的找到value，查找时间复杂度为0(1)，增加时间复杂度为0(1)。

哈希碰撞

  • 若干个不同元素通过hash函数映射成了用一个key。这样的话会导致访问该元素时间过慢

解决哈希碰撞的方法

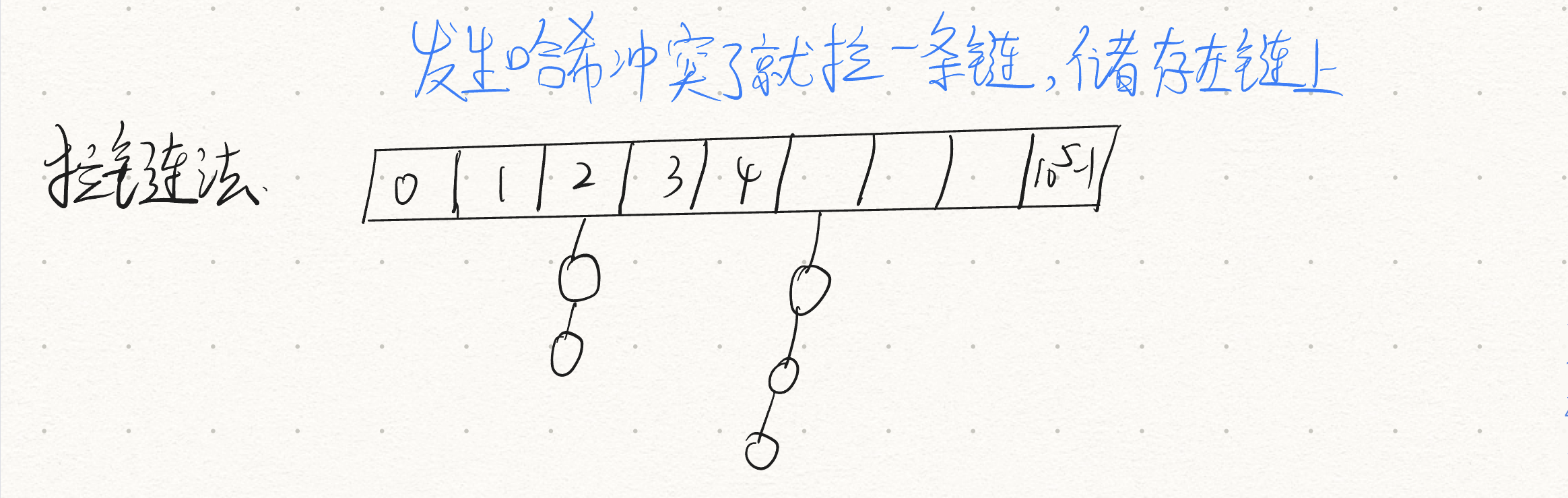
1. 拉链法

  • 方法简介:首先开一个一维数组来存储所有的哈希值,每一个凹槽上拉一条链(单链表)来存储这个槽上当前所有数

  • 一般情况下，算法题目不需要在哈希表中删除元素，一般只有添加和查找两个操作，如果真要删除，不是真正的删除，而是开一个数组打一个标记表示这个点被删除了

  • 当不断发生哈希碰撞时，就会拉成一条长链这样的话查询的时间复杂度就会变成线性的了（有时候题目会卡你的一定要注意了）

  • 题目链接:https://www.acwing.com/problem/content/842/

  • 代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
const int mod = 1e5 + 3;
string op;
int x, N;
int h[maxn], e[maxn], ne[maxn], idx;
/*
    插入操作时间复杂度o(1)
    插入步骤:
    1.通过哈希函数(这里是对x取模,这个mod得保证是质数这样才能尽可能避免哈希冲突)映射成k
    2.链表插入操作(这里是头插法)
*/
void insert(int x) {
    int k = (x % mod + mod) % mod;    //在c++中负数取模还是负数
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx;
    ++idx;
}
/*
    查找时间复杂度o(1)
    查找操作:
    1.通过哈希函数(这里是对x取模,这个mod得保证是质数这样才能尽可能避免哈希冲突)映射成k
    2.遍历链表查找x
*/
bool find(int x) {
    int k = (x % mod + mod) % mod;
    for (int i = h[k]; i != -1; i = ne[i]) {
        if (e[i] == x) return true;
    }
    return false;
}
/*
    删除操作不是真的删除,就是开个数组在需要删除的地方打个标记，时间复杂度o(1)
*/
int main(void) {
    //用-1来表示链表的末尾
    memset(h, -1, sizeof h);    //初始化别忘了
    cin >> N;
    while (N--) {
        cin >> op >> x;
        if (op == "I") {
            insert(x);
        }
        else {
            if (find(x)) {
                puts("Yes");
            }
            else {
                puts("No");
            }
        }
    }
}

2. 开放寻址法

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
const int mod = 2e5 + 3;      //取模的时候要为质数，这样的话可以减少哈希冲突
const int INF = 0x3f3f3f3f;   //标记该值是否被使用过,这个地方也可以取其他数,只要题目数据取不到就行
int h[maxn];                  //如果数组的值为INF表示这个位置是空的
string op;
int n, x;
/*
    该函数的作用是:
    1.返回x该插入的位置(插入)
    2.返回x应该在的位置(查找)
*/
int find(int x) {
    int k = (x % mod + mod) % mod;
    while (h[k] != INF && h[k] != x) {
        k++;
        if (k == maxn) k = 0;   //这步很关键得重头开始
    }
    /*
        当h[k] == INF时,即没有这个数,返回这个数应该插入的下标
        当h[k] == x时，即能找到x这个数,并返回下标
    */
    return k;
}

int main(void) {
    cin >> n;
    memset(h, 0x3f, sizeof h);              //一定要记得初始化
    while (n--) {
        cin >> op >> x;
        int k = find(x);
        if (op == "I") {
            h[k] = x;
        }
        else {
            if (h[k] == INF) puts("No");   //若是INF说明该位置上还没有元素
            else puts("Yes");
        }
    }
}

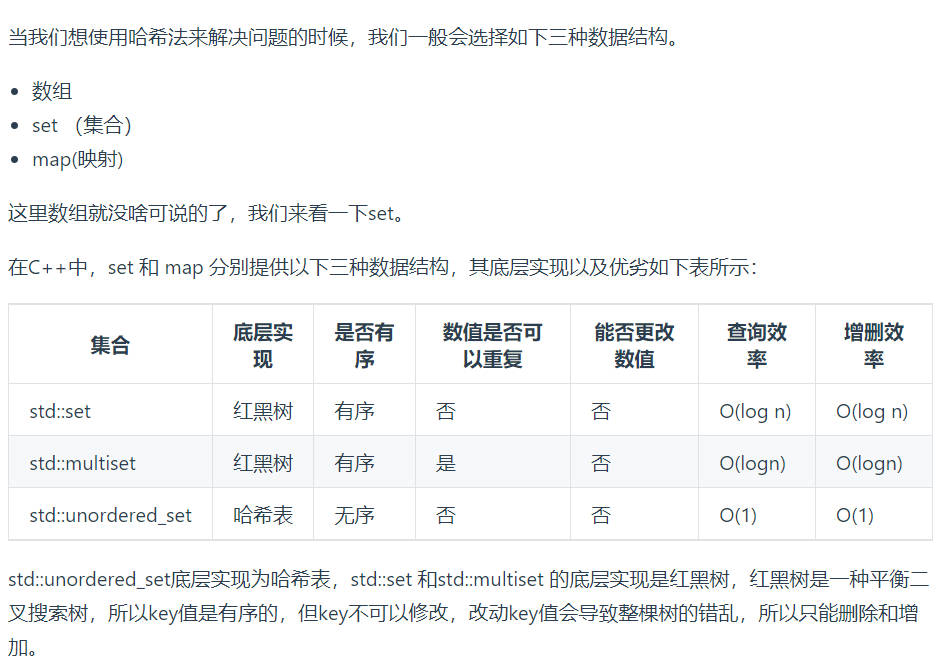
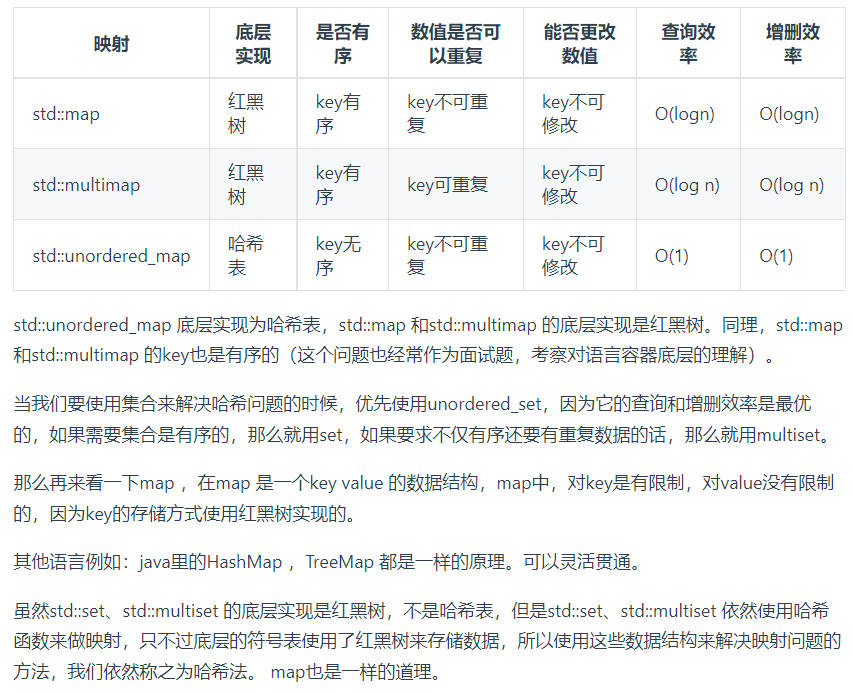
常见的三种哈希结构

  • 数组
  • set
  • map

posted @ 2022-07-13 11:35  SL霸霸  阅读(131)  评论(0)  编辑  收藏  举报