KMP算法关键

Knuth-Morris-Pratt Algorithm

 

当初写这个博客之后一年多，再次看发现当初并不是完全弄明白了。这里为了“避免重复制造轮子”，引用大神博客。

http://blog.csdn.net/v_july_v/article/details/7041827

 

特殊的 next[ ] 数组

 

next数组相当于“最大长度值”(前缀后缀的最大公共元素长度) 整体向右移动一位，然后初始值赋为-1

求next数组

	//优化过后的next 数组求法  
	void GetNextval(char* p, int next[])  
	{  
	    int pLen = strlen(p);  
	    next[0] = -1;  
	    int k = -1;  
	    int j = 0;  
	    while (j < pLen - 1)  
	    {  
	        //p[k]表示前缀，p[j]表示后缀    
	        if (k == -1 || p[j] == p[k])  
	        {  
	            ++j;  
	            ++k; 
	            if (p[j] != p[k])  
	                next[j] = k;   //之前只有这一行  
	            else  
	      //因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]  
	                next[j] = next[k];  
	        }  
	        else  
	        {  
	            k = next[k];  
	        }  
	    }  
	}  

 

 

注意：有了上面的这段代码效率更高

 

if (p[j] != p[k])  
	next[j] = k;   //之前只有这一行  
else  
	//因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]  
	next[j] = next[k];  

 

具体原理如下：

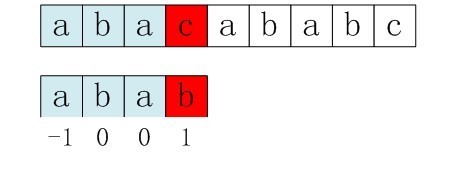
当两个字符串为下面所示的情况：

 

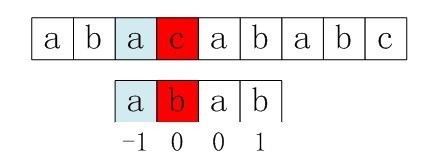
右移2位后，b又跟c失配。事实上，因为在上一步的匹配中，已经得知p[3] = b，与s[3] = c失配，而右移两位之后，让p[ next[3] ] =p[1] = b再跟s[3]匹配时，必然失配。问题出在哪呢？

 

匹配函数

 

	int KmpSearch(char* s, char* p)  
	{  
	    int i = 0;  
	    int j = 0;  
	    int sLen = strlen(s);  
	    int pLen = strlen(p);  
	    while (i < sLen && j < pLen)  
	    {  
	        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++      
	        if (j == -1 || s[i] == p[j])  
	        {  
	            i++;  
	            j++;  
	        }  
	        else  
	        {  
	            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]      
	            //next[j]即为j所对应的next值        
	            j = next[j];  
	        }  
	    }  
	    if (j == pLen)  
	        return i - j;  
	    else  
	        return -1;  
	}