吴恩达机器学习笔记59-向量化：低秩矩阵分解与均值归一化（Vectorization: Low Rank Matrix Factorization & Mean Normalization）
一、向量化：低秩矩阵分解
之前我们介绍了协同过滤算法，本节介绍该算法的向量化实现，以及说说有关该算法可以做的其他事情。
举例：
1.当给出一件产品时，你能否找到与之相关的其它产品。
2.一位用户最近看上一件产品，有没有其它相关的产品，你可以推荐给他。
我们将要做的是：实现一种选择的方法，写出协同过滤算法的预测情况。
我们有关于五部电影的数据集，我将要做的是，将这些用户的电影评分，进行分组并存
到一个矩阵中。
我们有五部电影，以及四位用户，那么 这个矩阵 𝑌 就是一个5 行4 列的矩阵，它将
这些电影的用户评分数据都存在矩阵里：
我们记：
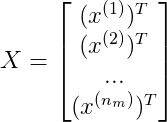
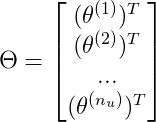
推出评分：
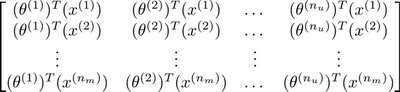
上述就是协同矩阵的向量化。
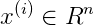
找出使两个商品特征比较相同的产品，即可以找出使得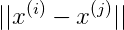
最小的五个商品，则这5个商品就是和i最相似的5个商品，既可以作为相关产品推荐。
二：均值归一化
假设有下面一组数据：
即有一个用户Eve没有对任何电影进行评价，这时候如果我们使用之前的方法测Eve对每部电影的评分，则最小化图上的公式，因为对于任意i，Eve都没有评分过，因此①式r(i, j)=1条件不满足，因此①对于最小化Eve的数据没有作用，②也没有作用，因此对于最小化Eve数据有作用的便是③式，即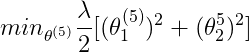
，因此二者都为0，因此
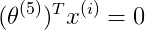于是对于Eve的预测评分都为0。
虽然结果是得出来了，但是这个结果我们没办法用来推荐，因为对所有的电影，其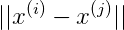
因此，我们引入归一化：
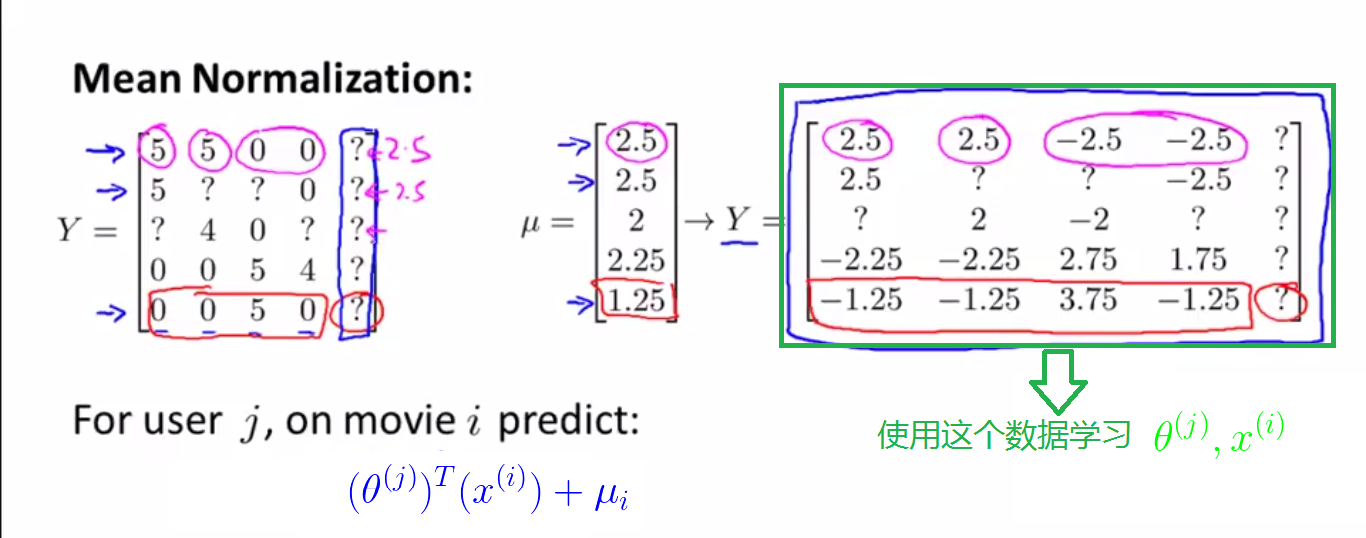
即对于某一部电影，利用已经评过分的值（？不计算在内），计算出平均分，记为μ，于是归一化矩阵为原来的Y的每一个数减去这一行（这一部电影）对应的平均值，得到新的Y，如上图右侧所示，利用这个新的Y矩阵学习θ和x的值。则对于Eve，之前关于最小化的分析仍成立，即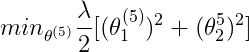
归一化之后的预测值公式为：
因此对于Eve的预测值为：
其实对于这个预测结果我们是可以接受的，因为我们不知道Eve的喜好，因此把她的评分预测为平均水平。
特殊情况：若出现有一部电影无评分的情况，则可以考虑使每列的均值为0，即计算每列的均值，用Y减去对应列的均值得到新的Y矩阵。
