吴恩达机器学习笔记49-主成分分析问题（Principal Component Analysis Problem Formulation）

　　主成分分析(PCA)是最常见的降维算法。

　　在PCA 中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据
都投射到该向量上时，我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点
的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

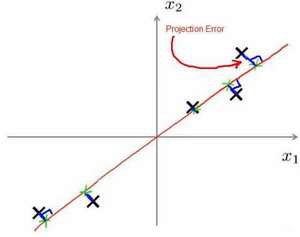
　　下面给出主成分分析问题的描述：
问题是要将𝑛维数据降至𝑘维，目标是找到向量𝑢(1) ,𝑢(2) ,...,𝑢(𝑘)使得总的投射误差最小。
　　主成分分析与线性回顾的比较：

　　主成分分析与线性回归是两种不同的算法。主成分分析最小化的是投射误差（Projected
Error），而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果，而主成分分析
不作任何预测。

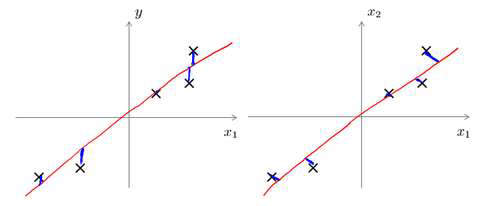
上图中，左边的是线性回归的误差（垂直于横轴投影），右边则是主要成分分析的误差
（垂直于红线投影）。

　　PCA 将𝑛个特征降维到𝑘个，可以用来进行数据压缩，如果100 维的向量最后可以用10
维来表示，那么压缩率为90%。同样图像处理领域的KL 变换使用PCA 做图像压缩。但PCA
要保证降维后，还要保证数据的特性损失最小。
　　PCA 技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要
性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模
型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
　　PCA 技术的一个很大的优点是，它是完全无参数限制的。在PCA 的计算过程中完全不
需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与
用户是独立的。
　　但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了
数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，
效率也不高。