吴恩达机器学习笔记47-K均值算法的优化目标、随机初始化与聚类数量的选择（Optimization Objective & Random Initialization & Choosing the Number of Clusters of K-Means Algorithm）

一、K均值算法的优化目标　　

　　K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，
因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

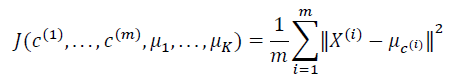
其中𝜇𝑐(𝑖)代表与𝑥(𝑖)最近的聚类中心点。 我们的的优化目标便是找出使得代价函数最小
的 𝑐(1),𝑐(2),...,𝑐(𝑚)和𝜇1,𝜇2,...,𝜇𝑘：

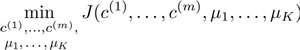
回顾刚才给出的: K-均值迭代算法，我们知道，第一个循环是用于减小𝑐(𝑖)引起的代价，
而第二个循环则是用于减小𝜇𝑖引起的代价。迭代的过程一定会是每一次迭代都在减小代价函
数，不然便是出现了错误。

二、随机初始化　　

　　在运行K-均值算法的之前，我们首先要随机初始化所有的聚类中心点：

1. 我们应该选择𝐾 < 𝑚，即聚类中心点的个数要小于所有训练集实例的数量
2. 随机选择𝐾个训练实例，然后令𝐾个聚类中心分别与这𝐾个训练实例相等

K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情
况。

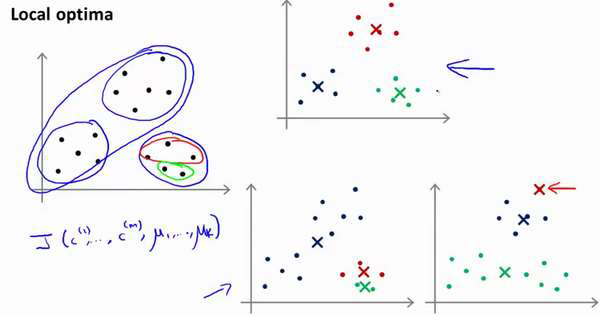
　　为了解决这个问题，我们通常需要多次运行K-均值算法，每一次都重新进行随机初始
化，最后再比较多次运行K-均值的结果，选择代价函数最小的结果。这种方法在𝐾较小的时
候（2--10）还是可行的，但是如果𝐾较大，这么做也可能不会有明显地改善

三、聚类数量的选择

　　没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。选
择的时候思考我们运用K-均值算法聚类的动机是什么，然后选择能最好服务于该目的标聚
类数。

 

　　当人们在讨论，选择聚类数目的方法时，有一个可能会谈及的方法叫作“肘部法则”。关
于“肘部法则”，我们所需要做的是改变𝐾值，也就是聚类类别数目的总数。我们用一个聚类
来运行K 均值聚类方法。这就意味着，所有的数据都会分到一个聚类里，然后计算成本函数
或者计算畸变函数𝐽。𝐾代表聚类数字。

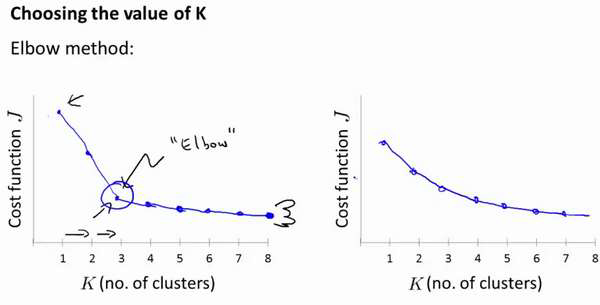
　　我们可能会得到一条类似于这样的曲线。像一个人的肘部。这就是“肘部法则”所做的，
让我们来看这样一个图，看起来就好像有一个很清楚的肘在那儿。好像人的手臂，如果你伸
出你的胳膊，那么这就是你的肩关节、肘关节、手。这就是“肘部法则”。你会发现这种模式，
它的畸变值会迅速下降，从1 到2，从2 到3 之后，你会在3 的时候达到一个肘点。在此之
后，畸变值就下降的非常慢，看起来就像使用3 个聚类来进行聚类是正确的，这是因为那个
点是曲线的肘点，畸变值下降得很快，𝐾 = 3之后就下降得很慢，那么我们就选𝐾 = 3。当你
应用“肘部法则”的时候，如果你得到了一个像上面这样的图，那么这将是一种用来选择聚类
个数的合理方法。

 

　　例如，我们的 T-恤制造例子中，我们要将用户按照身材聚类，我们可以分成3 个尺
寸:𝑆, 𝑀, 𝐿，也可以分成5 个尺寸𝑋𝑆, 𝑆, 𝑀, 𝐿, 𝑋𝐿，这样的选择是建立在回答“聚类后我们制造
的T-恤是否能较好地适合我们的客户”这个问题的基础上作出的。