吴恩达机器学习笔记43-SVM大边界分类背后的数学（Mathematics Behind Large Margin Classification of SVM）

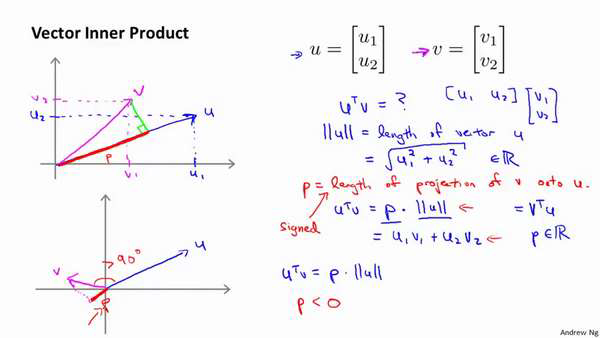
　　假设我有两个向量，𝑢和𝑣，我将它们写在这里。两个都是二维向量，我们看一下，𝑢𝑇 𝑣的结果。𝑢𝑇 𝑣也叫做向量𝑢和𝑣之间的内积。由于是二维向量，我可以将它们画在这个图上。

我们说，这就是向量𝑢即在横轴上，取值为某个𝑢1，而在纵轴上，高度是某个𝑢2作为𝑢的第二个分量。现在，很容易计算的一个量

就是向量𝑢的范数。∥𝑢∥表示𝑢的范数，即𝑢的长度，即向量𝑢的欧几里得长度。根据毕达哥拉
斯定理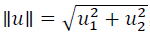， 这是向量𝑢的长度，它是一个实数。

　　现在让我们回头来看向量𝑣 ，因为我们想计算内积。𝑣是另一个向量，它的两个分量𝑣1
和𝑣2是已知的。向量𝑣可以画在这里，现在让我们来看看如何计算𝑢和𝑣之间的内积。这就是
具体做法，我们将向量𝑣投影到向量𝑢上，我们做一个直角投影，或者说一个90 度投影将其
投影到𝑢上，接下来我度量这条红线的长度。我称这条红线的长度为𝑝，因此𝑝就是长度，或
者说是向量𝑣投影到向量𝑢上的量，我将它写下来，𝑝是𝑣投影到向量𝑢上的长度，因此可以将

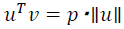或者说𝑢的长度。这是计算内积的一种方法。如果你从几何上画出p 的值，同

时画出𝑢的范数，你也会同样地计算出内积，答案是一样的。另一个计算公式是：𝑢𝑇 𝑣就是
[𝑢1 𝑢2] 这个一行两列的矩阵乘以𝑣。因此可以得到𝑢1 × 𝑣1 + 𝑢2 × 𝑣2。根据线性代数的知识，
这两个公式会给出同样的结果。顺便说一句，𝑢𝑇 𝑣 = 𝑣𝑇𝑢。因此如果你将𝑢和𝑣交换位置，将
𝑢投影到𝑣上，而不是将𝑣投影到𝑢上，然后做同样地计算，只是把𝑢和𝑣的位置交换一下，你
事实上可以得到同样的结果。申明一点，在这个等式中𝑢的范数是一个实数，𝑝也是一个实
数，因此𝑢𝑇 𝑣就是两个实数正常相乘。

　　最后一点，需要注意的就是𝑝值，𝑝事实上是有符号的，即它可能是正值，也可能是负值。
我的意思是说，如果𝑢是一个类似这样的向量，𝑣是一个类似这样的向量，𝑢和𝑣之间的夹角
大于90 度，则如果将𝑣投影到𝑢上，会得到这样的一个投影，这是𝑝的长度，在这个情形下
我们仍然有𝑢𝑇 𝑣是等于𝑝乘以𝑢的范数。唯一一点不同的是𝑝在这里是负的。在内积计算中，
如果𝑢和𝑣之间的夹角小于90 度，那么那条红线的长度𝑝是正值。然而如果这个夹角大于90
度，则𝑝将会是负的。就是这个小线段的长度是负的。如果它们之间的夹角大于90 度，两个
向量之间的内积也是负的。这就是关于向量内积的知识。我们接下来将会使用这些关于向量
内积的性质试图来理解支持向量机中的目标函数。

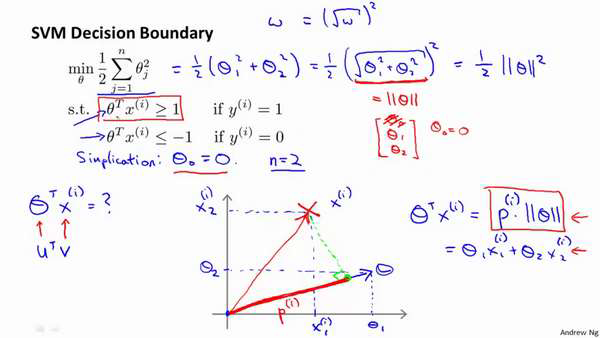
我接下来忽略掉截距，令𝜃0 = 0，这样更容易画示意图。我将特征数𝑛置为2，因此我们
仅有两个特征𝑥1, 𝑥2，现在我们来看一下目标函数，支持向量机的优化目标函数。当我们仅
有两个特征，即𝑛 = 2时，这个式子可以写作：

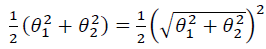
　　我们只有两个参数𝜃1, 𝜃2。你可能注意到括号里面的这一项是向量𝜃的范数，或者说是向量𝜃的长度。我的

意思是如果我们将向量𝜃写出来，那么我刚刚画红线的这一项就是向量𝜃的长度或范数。这
里我们用的是之前学过的向量范数的定义，事实上这就等于向量𝜃的长度。

当然你可以将其写作𝜃0, 𝜃1, 𝜃2，如果𝜃0 = 0，那就是𝜃1, 𝜃2的长度。在这里我将忽略𝜃0，
这样来写𝜃的范数，它仅仅和𝜃1, 𝜃2有关。但是，数学上不管你是否包含，其实并没有差别，
因此在我们接下来的推导中去掉𝜃0不会有影响这意味着我们的目标函数是等于

因此
支持向量机做的全部事情，就是极小化参数向量𝜃范数的平方，或者说长度的平方。

现在我将要看看这些项：𝜃𝑇𝑥更深入地理解它们的含义。给定参数向量𝜃给定一个样本
𝑥，这等于什么呢?在前一页幻灯片上，我们画出了在不同情形下，𝑢𝑇 𝑣的示意图，我们将会
使用这些概念，𝜃和𝑥(𝑖)就类似于𝑢和𝑣 。

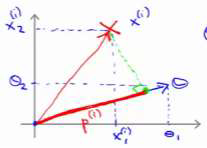
　　让我们看一下示意图：我们考察一个单一的训练样本，我有一个正样本在这里，用一个
叉来表示这个样本𝑥(𝑖)，意思是在水平轴上取值为𝑥1(𝑖)，在竖直轴上取值为𝑥2(𝑖)。这就是我画出的训练样本。尽管我没有将其真的看做向量。

它事实上就是一个始于原点，终点位置在这个训练样本点的向量。现在，我们有一个参数向量我会将它也画成向量。我将𝜃1画在横轴这里，将𝜃2 画在纵轴这里，那么内积𝜃𝑇𝑥(𝑖) 将会是什么呢？

　　使用我们之前的方法，我们计算的方式就是我将训练样本投影到参数向量𝜃，然后我来
看一看这个线段的长度，我将它画成红色。我将它称为𝑝(𝑖)用来表示这是第 𝑖个训练样本在
参数向量𝜃上的投影。根据我们之前幻灯片的内容，我们知道的是𝜃𝑇𝑥(𝑖)将会等于𝑝 乘以向
量 𝜃 的长度或范数。这就等于𝜃1 ⋅ 𝑥1(𝑖) + 𝜃2 ⋅ 𝑥2(𝑖)。这两种方式是等价的，都可以用来计算𝜃和𝑥(𝑖)之间的内积。

这告诉了我们什么呢？这里表达的意思是：这个𝜃𝑇𝑥(𝑖) >= 1 或者𝜃𝑇𝑥(𝑖) < −1的,约束
是可以被𝑝(𝑖) ⋅ ∥𝜃∥ >= 1这个约束所代替的。因为𝜃𝑇𝑥(𝑖) = 𝑝(𝑖) ⋅ ∥𝜃∥ ，将其写入我们的优化目标。我们将会得到没有了约束，𝜃𝑇𝑥(𝑖)而变成了𝑝(𝑖) ⋅ ∥𝜃∥。

需要提醒一点，我们之前曾讲过这个优化目标函数可以被写成等于。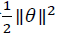

　　现在让我们考虑下面这里的训练样本。现在，继续使用之前的简化，即𝜃0 = 0，我们来
看一下支持向量机会选择什么样的决策界。这是一种选择，我们假设支持向量机会选择这个
决策边界。这不是一个非常好的选择，因为它的间距很小。这个决策界离训练样本的距离很
近。我们来看一下为什么支持向量机不会选择它。

　　对于这样选择的参数𝜃，可以看到参数向量𝜃事实上是和决策界是90 度正交的，因此这
个绿色的决策界对应着一个参数向量𝜃这个方向,顺便提一句𝜃0 = 0的简化仅仅意味着决策
界必须通过原点(0,0)。现在让我们看一下这对于优化目标函数意味着什么。

　　比如这个样本，我们假设它是我的第一个样本𝑥(1)，如果我考察这个样本到参数𝜃的投
影，投影是这个短的红线段，就等于𝑝(1)，它非常短。类似地，这个样本如果它恰好是𝑥(2)，
我的第二个训练样本，则它到𝜃的投影在这里。我将它画成粉色，这个短的粉色线段是𝑝(2)，
即第二个样本到我的参数向量𝜃的投影。因此，这个投影非常短。𝑝(2)事实上是一个负值，
𝑝(2)是在相反的方向，这个向量和参数向量𝜃的夹角大于90 度，𝑝(2)的值小于0。

　　我们会发现这些𝑝(𝑖)将会是非常小的数，因此当我们考察优化目标函数的时候，对于正
样本而言，我们需要𝑝(𝑖) ⋅ ∥𝜃∥ >= 1,但是如果 𝑝(𝑖)在这里非常小,那就意味着我们需要𝜃的范
数非常大.因为如果 𝑝(1) 很小,而我们希望𝑝(1) ⋅ ∥𝜃∥ >= 1 ,令其实现的唯一的办法就是这两
个数较大。如果 𝑝(1) 小，我们就希望𝜃的范数大。类似地，对于负样本而言我们需要𝑝(2) ⋅
∥𝜃∥ <= −1。我们已经在这个样本中看到𝑝(2)会是一个非常小的数，因此唯一的办法就是𝜃的
范数变大。但是我们的目标函数是希望找到一个参数𝜃，它的范数是小的。因此，这看起来
不像是一个好的参数向量𝜃的选择。

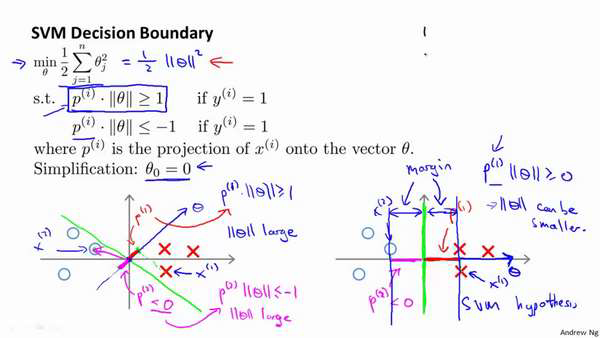
　　相反的，来看一个不同的决策边界。比如说，支持向量机选择了这个决策界，现在状况
会有很大不同。如果这是决策界，这就是相对应的参数𝜃的方向，因此，在这个决策界之下，
垂直线是决策界。使用线性代数的知识，可以说明，这个绿色的决策界有一个垂直于它的向
量𝜃。现在如果你考察你的数据在横轴𝑥上的投影，比如这个我之前提到的样本，我的样本
𝑥(1)，当我将它投影到横轴𝑥上，或说投影到𝜃上，就会得到这样𝑝(1)。它的长度是𝑝(1)，另一
个样本，那个样本是𝑥(2)。我做同样的投影，我会发现，𝑝(2)的长度是负值。你会注意到现在
𝑝(1) 和𝑝(2)这些投影长度是长多了。如果我们仍然要满足这些约束，𝑃(𝑖) ⋅ ∥𝜃∥>1，则因为𝑝(1)
变大了，𝜃的范数就可以变小了。因此这意味着通过选择右边的决策界，而不是左边的那个，
支持向量机可以使参数𝜃的范数变小很多。因此，如果我们想令𝜃的范数变小，从而令𝜃范数
的平方变小，就能让支持向量机选择右边的决策界。这就是支持向量机如何能有效地产生大
间距分类的原因。

　　看这条绿线，这个绿色的决策界。我们希望正样本和负样本投影到𝜃的值大。要做到这
一点的唯一方式就是选择这条绿线做决策界。这是大间距决策界来区分开正样本和负样本这
个间距的值。这个间距的值就是𝑝(1), 𝑝(2), 𝑝(3)等等的值。通过让间距变大，即通过这些
𝑝(1), 𝑝(2), 𝑝(3)等等的值，支持向量机最终可以找到一个较小的𝜃范数。这正是支持向量机中
最小化目标函数的目的。

　　以上就是为什么支持向量机最终会找到大间距分类器的原因。因为它试图极大化这些
𝑝(𝑖)的范数，它们是训练样本到决策边界的距离。最后一点，我们的推导自始至终使用了这
个简化假设，就是参数𝜃0 = 0。

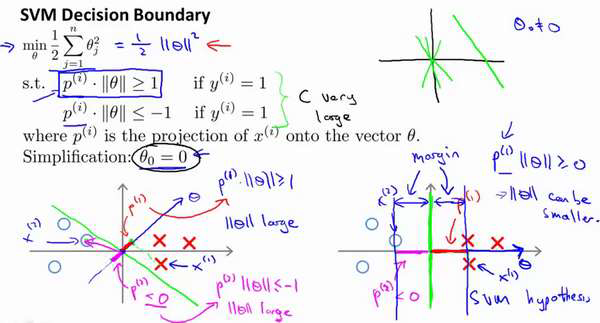
　　就像我之前提到的。这个的作用是：𝜃0 = 0的意思是我们让决策界通过原点。如果你令
𝜃0不是0 的话，含义就是你希望决策界不通过原点。我将不会做全部的推导。实际上，支持
向量机产生大间距分类器的结论，会被证明同样成立，证明方式是非常类似的，是我们刚刚
做的证明的推广。

　　之前视频中说过，即便𝜃0不等于0，支持向量机要做的事情都是优化这个目标函数对应
着𝐶值非常大的情况，但是可以说明的是，即便𝜃0不等于0，支持向量机仍然会找到正样本
和负样本之间的大间距分隔。