吴恩达机器学习笔记17-逻辑回归的代价函数

　　在这段视频中，我们要介绍如何拟合逻辑回归模型的参数𝜃。具体来说，我要定义用来
拟合参数的优化目标或者叫代价函数，这便是监督学习问题中的逻辑回归模型的拟合问题。

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们
也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将带入到这样

定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。

　　这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。
线性回归的代价函数为：

 

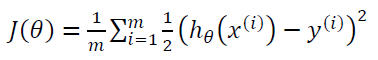
我们重新定义逻辑回归的代价函数为：

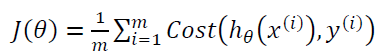，其中

ℎ𝜃 (𝑥)与 𝐶𝑜𝑠𝑡(ℎ𝜃(𝑥), 𝑦)之间的关系如下图所示：

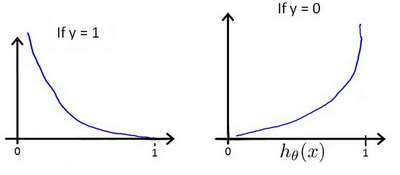
　　这样构建的𝐶𝑜𝑠𝑡(ℎ𝜃(𝑥), 𝑦)函数的特点是：当实际的 𝑦 = 1 且ℎ𝜃(𝑥)也为 1 时误差为 0，
当 𝑦 = 1 但ℎ𝜃 (𝑥)不为1 时误差随着ℎ𝜃 (𝑥)变小而变大；当实际的 𝑦 = 0 且ℎ𝜃(𝑥)也为 0 时
代价为 0，当𝑦 = 0 但ℎ𝜃(𝑥)不为 0 时误差随着 ℎ𝜃 (𝑥)的变大而变大。
将构建的 𝐶𝑜𝑠𝑡(ℎ𝜃 (𝑥), 𝑦)简化如下：

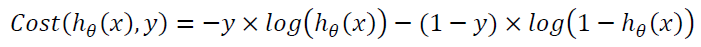
带入代价函数得到：

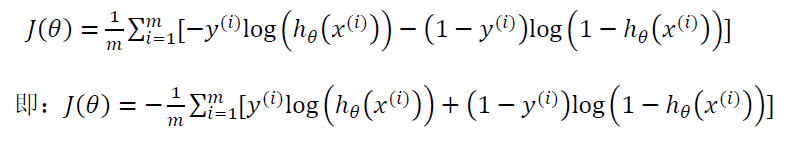
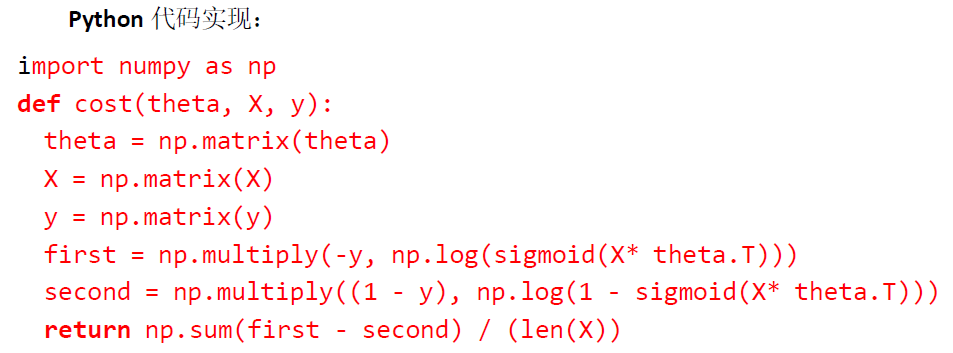
　　在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的
参数了。算法为：

　　在这个视频中，我们定义了单训练样本的代价函数，凸性分析的内容是超出这门课的范
围的，但是可以证明我们所选的代价值函数会给我们一个凸优化问题。代价函数𝐽(𝜃)会是一
个凸函数，并且没有局部最优值。
代价函数求偏导的推导过程：

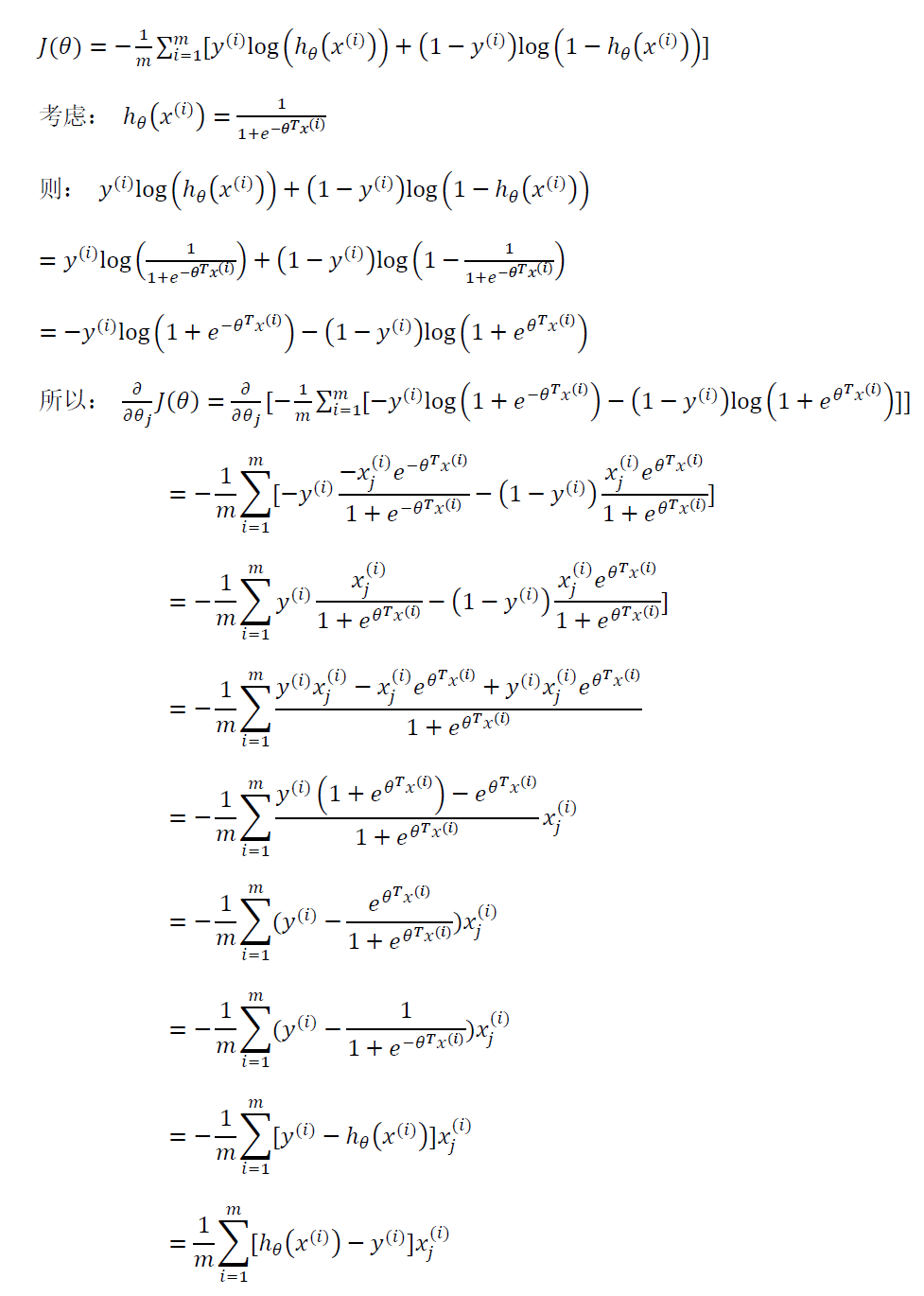
注：虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里
的ℎ𝜃(𝑥) = 𝑔(𝜃𝑇𝑋)与线性回归中不同，所以实际上是不一样的。另外，在运行梯度下降算法
之前，进行特征缩放依旧是非常必要的。