吴恩达机器学习笔记13-正规方程(Normal Equation)

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法
是更好的解决方案。如：

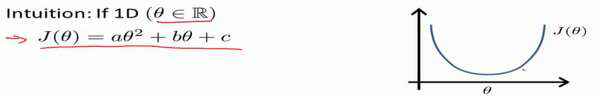
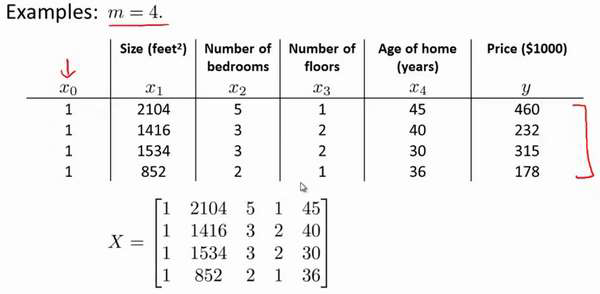
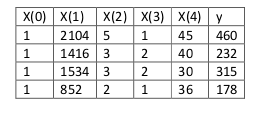
即：

运用正规方程方法求解参数：

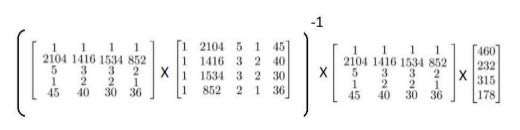
注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺
寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是
不能用的。

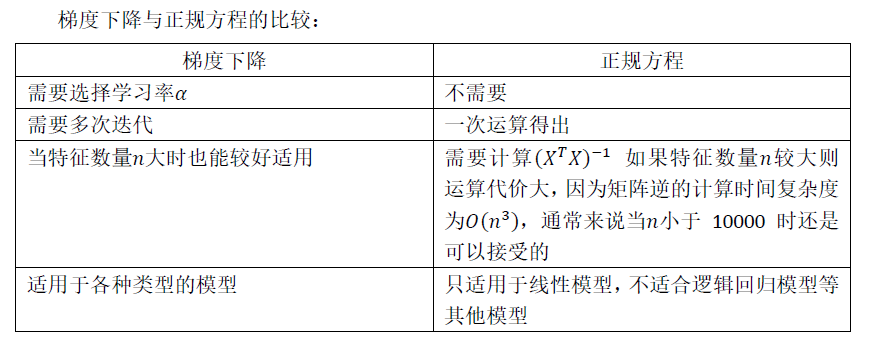
　　总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数𝜃的替代方法。
具体地说，只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法。
　　随着我们要讲的学习算法越来越复杂，例如，当我们讲到分类算法，像逻辑回归算法，
我们会看到，实际上对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法，
我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有
大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为标
准方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，标准方程法是一个
比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种
算法都是值得学习的。