吴恩达机器学习笔记5-梯度下降I（Gradient descent intuition）

　　梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数
𝐽(𝜃0, 𝜃1) 的最小值。
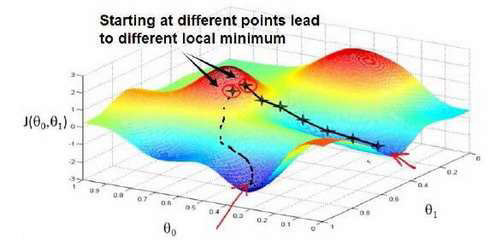
　　梯度下降背后的思想是：开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛)，计算代
价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到
到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确
定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组
合，可能会找到不同的局部最小值。

　　批量梯度下降（batch gradient descent）算法的公式为：

　　

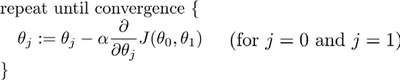
　　其中𝑎是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向
向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率
乘以代价函数的导数。

 

 

　　在梯度下降算法中，还有一个更微妙的问题，梯度下降中，我们要更新𝜃0和𝜃1 ，当 𝑗 =
0 和𝑗 = 1时，会产生更新，所以你将更新𝐽(𝜃0)和𝐽(𝜃1)。实现梯度下降算法的微妙之处是，
在这个表达式中，如果你要更新这个等式，你需要同时更新𝜃0和𝜃1，我的意思是在这个等式
中，我们要这样更新：
　　𝜃0:= 𝜃0 ，并更新𝜃1:= 𝜃1。
　　实现方法是：你应该计算公式右边的部分，通过那一部分计算出𝜃0和𝜃1的值，然后同时
更新𝜃0和𝜃1。