堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。
因此，学习堆排序之前，有必要了解堆！若读者不熟悉堆，建议先了解堆(建议可以通过二叉堆，左倾堆，斜堆，二项堆或斐波那契堆等文章进行了解)，然后再来学习本章。

我们知道，堆分为"最大堆"和"最小堆"。最大堆通常被用来进行"升序"排序，而最小堆通常被用来进行"降序"排序。
鉴于最大堆和最小堆是对称关系，理解其中一种即可。本文将对最大堆实现的升序排序进行详细说明。

最大堆进行升序排序的基本思想：
① 初始化堆：将数列a[1...n]构造成最大堆。
② 交换数据：将a[1]和a[n]交换，使a[n]是a[1...n]中的最大值；然后将a[1...n-1]重新调整为最大堆。接着，将a[1]和a[n-1]交换，使a[n-1]是a[1...n-1]中的最大值；然后将a[1...n-2]重新调整为最大值。依次类推，直到整个数列都是有序的。

下面，通过图文来解析堆排序的实现过程。注意实现中用到了"数组实现的二叉堆的性质"。
在第一个元素的索引为 0 的情形中：
性质一：索引为i的左孩子的索引是 (2*i+1);
性质二：索引为i的左孩子的索引是 (2*i+2);
性质三：索引为i的父结点的索引是 floor((i-1)/2);

例如，对于最大堆{110,100,90,40,80,20,60,10,30,50,70}而言：索引为0的左孩子的所有是1；索引为0的右孩子是2；索引为8的父节点是3。

堆排序图文说明

堆排序(升序)代码

/* 
 * (最大)堆的向下调整算法
 *
 * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 *
 * 参数说明：
 *     a -- 待排序的数组
 *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 */
void maxheap_down(int a[], int start, int end)
{
    int c = start;            // 当前(current)节点的位置
    int l = 2*c + 1;        // 左(left)孩子的位置
    int tmp = a[c];            // 当前(current)节点的大小
    for (; l <= end; c=l,l=2*l+1)
    {
        // "l"是左孩子，"l+1"是右孩子
        if ( l < end && a[l] < a[l+1])
            l++;        // 左右两孩子中选择较大者，即m_heap[l+1]
        if (tmp >= a[l])
            break;        // 调整结束
        else            // 交换值
        {
            a[c] = a[l];
            a[l]= tmp;
        }
    }
}

/*
 * 堆排序(从小到大)
 *
 * 参数说明：
 *     a -- 待排序的数组
 *     n -- 数组的长度
 */
void heap_sort_asc(int a[], int n)
{
    int i;

    // 从(n/2-1) --> 0逐次遍历。遍历之后，得到的数组实际上是一个(最大)二叉堆。
    for (i = n / 2 - 1; i >= 0; i--)
        maxheap_down(a, i, n-1);

    // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
    for (i = n - 1; i > 0; i--)
    {
        // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最大的。
        swap(a[0], a[i]);
        // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最大堆。
        // 即，保证a[i-1]是a[0...i-1]中的最大值。
        maxheap_down(a, 0, i-1);
    }
}

heap_sort_asc(a, n)的作用是：对数组a进行升序排序；其中，a是数组，n是数组长度。
heap_sort_asc(a, n)的操作分为两部分：初始化堆和交换数据。
maxheap_down(a, start, end)是最大堆的向下调整算法。

下面演示heap_sort_asc(a, n)对a={20,30,90,40,70,110,60,10,100,50,80}, n=11进行堆排序过程。下面是数组a对应的初始化结构：

1 初始化堆

在堆排序算法中，首先要将待排序的数组转化成二叉堆。
下面演示将数组{20,30,90,40,70,110,60,10,100,50,80}转换为最大堆{110,100,90,40,80,20,60,10,30,50,70}的步骤。

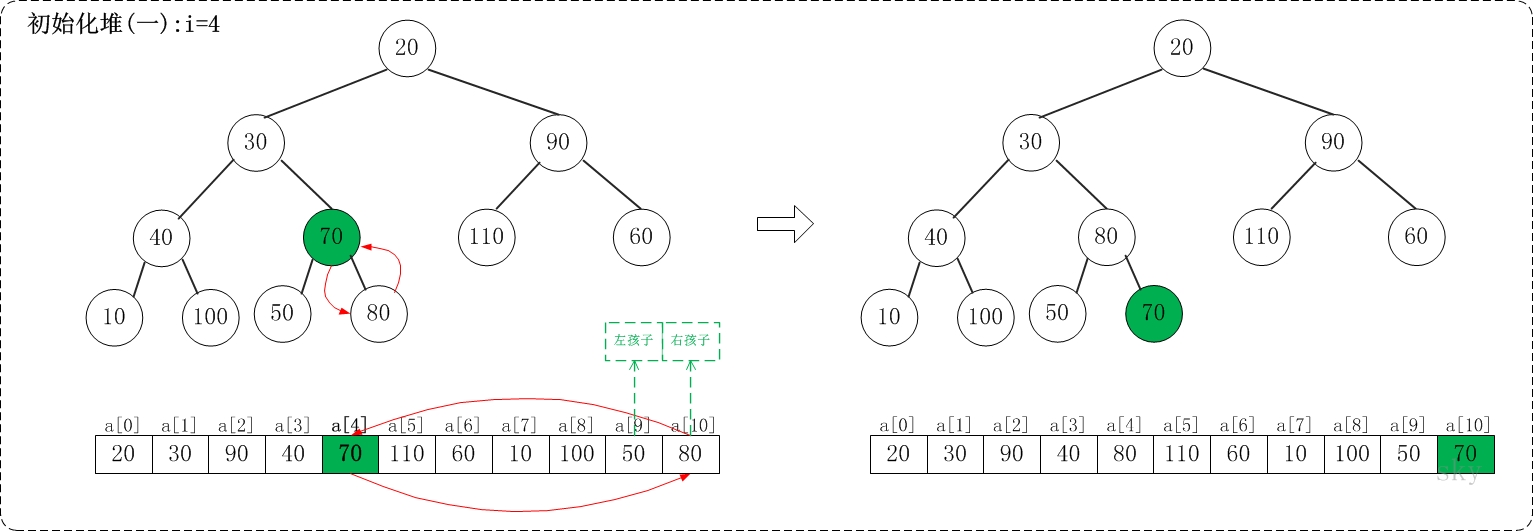
1.1 i=11/2-1，即i=4

上面是maxheap_down(a, 4, 9)调整过程。maxheap_down(a, 4, 9)的作用是将a[4...9]进行下调；a[4]的左孩子是a[9]，右孩子是a[10]。调整时，选择左右孩子中较大的一个(即a[10])和a[4]交换。

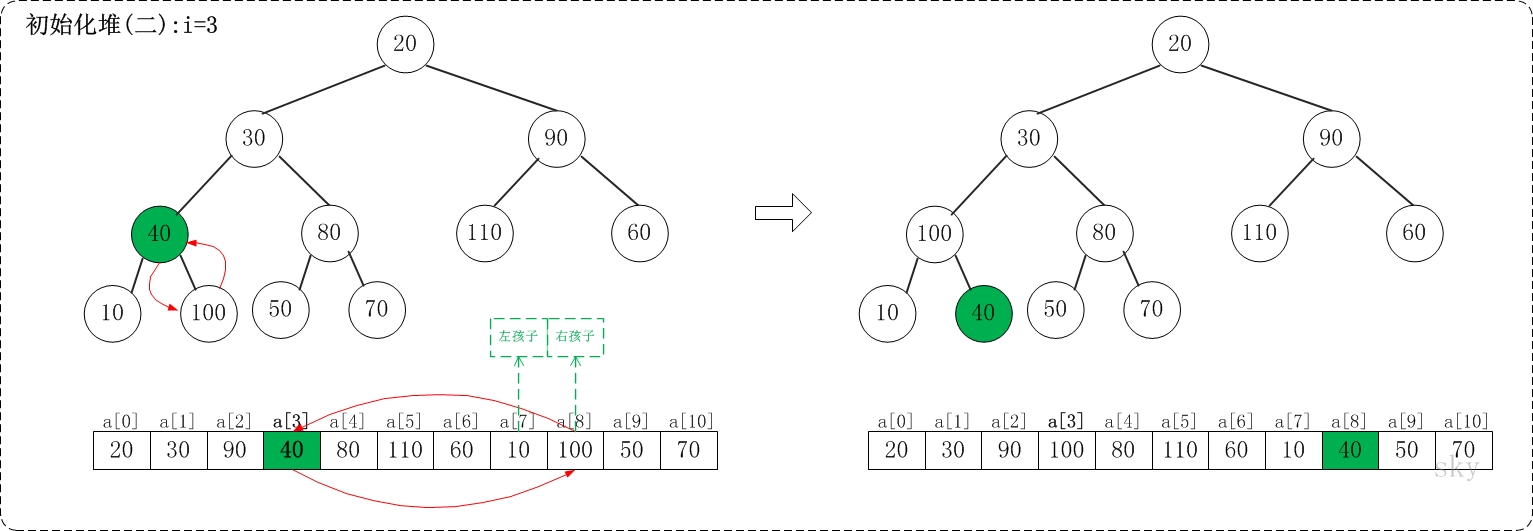
1.2 i=3

上面是maxheap_down(a, 3, 9)调整过程。maxheap_down(a, 3, 9)的作用是将a[3...9]进行下调；a[3]的左孩子是a[7]，右孩子是a[8]。调整时，选择左右孩子中较大的一个(即a[8])和a[4]交换。

1.3 i=2

上面是maxheap_down(a, 2, 9)调整过程。maxheap_down(a, 2, 9)的作用是将a[2...9]进行下调；a[2]的左孩子是a[5]，右孩子是a[6]。调整时，选择左右孩子中较大的一个(即a[5])和a[2]交换。

1.4 i=1

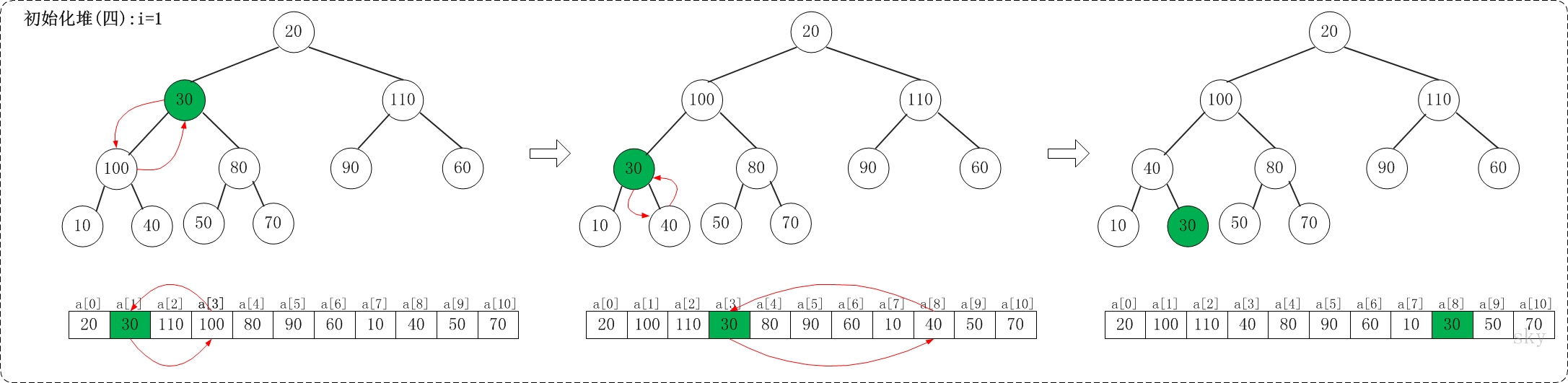
上面是maxheap_down(a, 1, 9)调整过程。maxheap_down(a, 1, 9)的作用是将a[1...9]进行下调；a[1]的左孩子是a[3]，右孩子是a[4]。调整时，选择左右孩子中较大的一个(即a[3])和a[1]交换。交换之后，a[3]为30，它比它的右孩子a[8]要大，接着，再将它们交换。

1.5 i=0

上面是maxheap_down(a, 0, 9)调整过程。maxheap_down(a, 0, 9)的作用是将a[0...9]进行下调；a[0]的左孩子是a[1]，右孩子是a[2]。调整时，选择左右孩子中较大的一个(即a[2])和a[0]交换。交换之后，a[2]为20，它比它的左右孩子要大，选择较大的孩子(即左孩子)和a[2]交换。

调整完毕，就得到了最大堆。此时，数组{20,30,90,40,70,110,60,10,100,50,80}也就变成了{110,100,90,40,80,20,60,10,30,50,70}。

第2部分交换数据

在将数组转换成最大堆之后，接着要进行交换数据，从而使数组成为一个真正的有序数组。
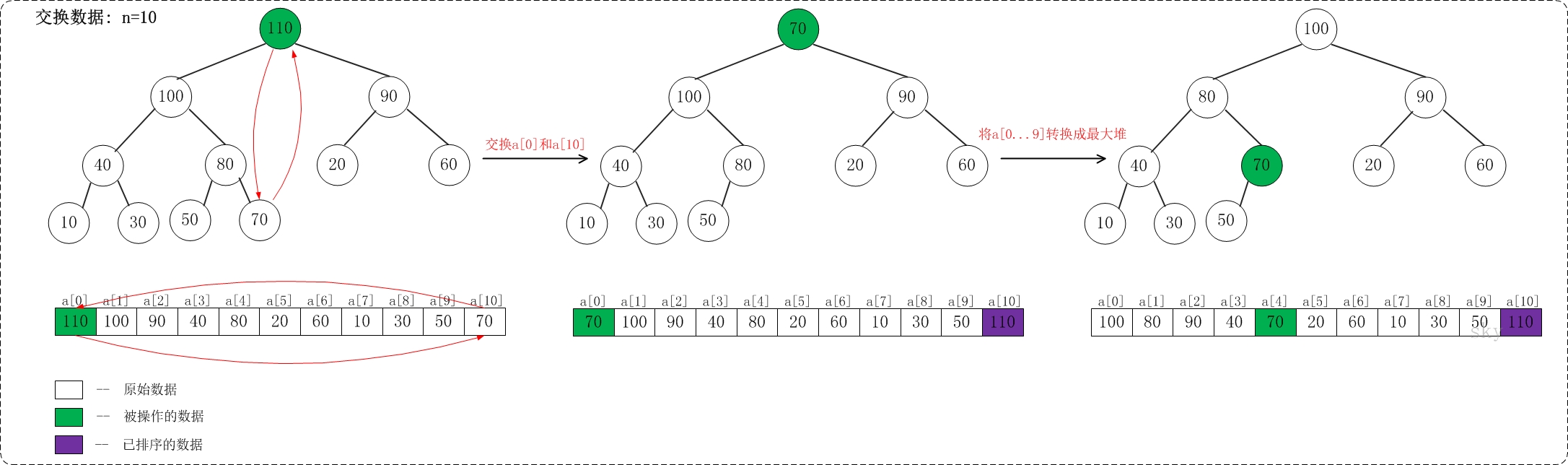
交换数据部分相对比较简单，下面仅仅给出将最大值放在数组末尾的示意图。

上面是当n=10时，交换数据的示意图。
当n=10时，首先交换a[0]和a[10]，使得a[10]是a[0...10]之间的最大值；然后，调整a[0...9]使它称为最大堆。交换之后：a[10]是有序的！
当n=9时，首先交换a[0]和a[9]，使得a[9]是a[0...9]之间的最大值；然后，调整a[0...8]使它称为最大堆。交换之后：a[9...10]是有序的！
...
依此类推，直到a[0...10]是有序的。

堆排序的时间复杂度和稳定性

堆排序时间复杂度
堆排序的时间复杂度是O(N*lgN)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？
堆排序是采用的二叉堆进行排序的，二叉堆就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是lg(N+1)。最多是多少呢？由于二叉堆是完全二叉树，因此，它的深度最多也不会超过lg(2N)。因此，遍历一趟的时间复杂度是O(N)，而遍历次数介于lg(N+1)和lg(2N)之间；因此得出它的时间复杂度是O(N*lgN)。

堆排序稳定性
堆排序是不稳定的算法，它不满足稳定算法的定义。它在交换数据的时候，是比较父结点和子节点之间的数据，所以，即便是存在两个数值相等的兄弟节点，它们的相对顺序在排序也可能发生变化。
算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

堆排序实现

下面给出堆排序的三种实现：C、C++和Java。这三种实现的原理和输出结果都是一样的，每一种实现中都包括了"最大堆对应的升序排列"和"最小堆对应的降序排序"。
堆排序C实现
实现代码(heap_sort.c)

  1 /**
  2  * 堆排序：C 语言
  3  *
  4  * @author skywang
  5  * @date 2014/03/12
  6  */
  7 
  8 #include <stdio.h>
  9 
 10 // 数组长度
 11 #define LENGTH(array) ( (sizeof(array)) / (sizeof(array[0])) )
 12 #define swap(a,b) (a^=b,b^=a,a^=b)
 13 
 14 /* 
 15  * (最大)堆的向下调整算法
 16  *
 17  * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 18  *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 19  *
 20  * 参数说明：
 21  *     a -- 待排序的数组
 22  *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 23  *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 24  */
 25 void maxheap_down(int a[], int start, int end)
 26 {
 27     int c = start;            // 当前(current)节点的位置
 28     int l = 2*c + 1;        // 左(left)孩子的位置
 29     int tmp = a[c];            // 当前(current)节点的大小
 30     for (; l <= end; c=l,l=2*l+1)
 31     {
 32         // "l"是左孩子，"l+1"是右孩子
 33         if ( l < end && a[l] < a[l+1])
 34             l++;        // 左右两孩子中选择较大者，即m_heap[l+1]
 35         if (tmp >= a[l])
 36             break;        // 调整结束
 37         else            // 交换值
 38         {
 39             a[c] = a[l];
 40             a[l]= tmp;
 41         }
 42     }
 43 }
 44 
 45 /*
 46  * 堆排序(从小到大)
 47  *
 48  * 参数说明：
 49  *     a -- 待排序的数组
 50  *     n -- 数组的长度
 51  */
 52 void heap_sort_asc(int a[], int n)
 53 {
 54     int i;
 55 
 56     // 从(n/2-1) --> 0逐次遍历。遍历之后，得到的数组实际上是一个(最大)二叉堆。
 57     for (i = n / 2 - 1; i >= 0; i--)
 58         maxheap_down(a, i, n-1);
 59 
 60     // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
 61     for (i = n - 1; i > 0; i--)
 62     {
 63         // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最大的。
 64         swap(a[0], a[i]);
 65         // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最大堆。
 66         // 即，保证a[i-1]是a[0...i-1]中的最大值。
 67         maxheap_down(a, 0, i-1);
 68     }
 69 }
 70 
 71 /* 
 72  * (最小)堆的向下调整算法
 73  *
 74  * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 75  *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 76  *
 77  * 参数说明：
 78  *     a -- 待排序的数组
 79  *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 80  *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 81  */
 82 void minheap_down(int a[], int start, int end)
 83 {
 84     int c = start;            // 当前(current)节点的位置
 85     int l = 2*c + 1;        // 左(left)孩子的位置
 86     int tmp = a[c];            // 当前(current)节点的大小
 87     for (; l <= end; c=l,l=2*l+1)
 88     {
 89         // "l"是左孩子，"l+1"是右孩子
 90         if ( l < end && a[l] > a[l+1])
 91             l++;        // 左右两孩子中选择较小者
 92         if (tmp <= a[l])
 93             break;        // 调整结束
 94         else            // 交换值
 95         {
 96             a[c] = a[l];
 97             a[l]= tmp;
 98         }
 99     }
100 }
101 
102 /*
103  * 堆排序(从大到小)
104  *
105  * 参数说明：
106  *     a -- 待排序的数组
107  *     n -- 数组的长度
108  */
109 void heap_sort_desc(int a[], int n)
110 {
111     int i;
112 
113     // 从(n/2-1) --> 0逐次遍历每。遍历之后，得到的数组实际上是一个最小堆。
114     for (i = n / 2 - 1; i >= 0; i--)
115         minheap_down(a, i, n-1);
116 
117     // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
118     for (i = n - 1; i > 0; i--)
119     {
120         // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最小的。
121         swap(a[0], a[i]);
122         // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最小堆。
123         // 即，保证a[i-1]是a[0...i-1]中的最小值。
124         minheap_down(a, 0, i-1);
125     }
126 }
127 
128 void main()
129 {
130     int i;
131     int a[] = {20,30,90,40,70,110,60,10,100,50,80};
132     int ilen = LENGTH(a);
133 
134     printf("before sort:");
135     for (i=0; i<ilen; i++)
136         printf("%d ", a[i]);
137     printf("\n");
138 
139     heap_sort_asc(a, ilen);            // 升序排列
140     //heap_sort_desc(a, ilen);        // 降序排列
141 
142     printf("after  sort:");
143     for (i=0; i<ilen; i++)
144         printf("%d ", a[i]);
145     printf("\n");
146 }

View Code

堆排序C++实现
实现代码(HeapSort.cpp)

  1 /**
  2  * 堆排序：C++
  3  *
  4  * @author skywang
  5  * @date 2014/03/11
  6  */
  7 
  8 #include <iostream>
  9 using namespace std;
 10 
 11 /* 
 12  * (最大)堆的向下调整算法
 13  *
 14  * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 15  *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 16  *
 17  * 参数说明：
 18  *     a -- 待排序的数组
 19  *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 20  *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 21  */
 22 void maxHeapDown(int* a, int start, int end)
 23 {
 24     int c = start;            // 当前(current)节点的位置
 25     int l = 2*c + 1;        // 左(left)孩子的位置
 26     int tmp = a[c];            // 当前(current)节点的大小
 27     for (; l <= end; c=l,l=2*l+1)
 28     {
 29         // "l"是左孩子，"l+1"是右孩子
 30         if ( l < end && a[l] < a[l+1])
 31             l++;        // 左右两孩子中选择较大者，即m_heap[l+1]
 32         if (tmp >= a[l])
 33             break;        // 调整结束
 34         else            // 交换值
 35         {
 36             a[c] = a[l];
 37             a[l]= tmp;
 38         }
 39     }
 40 }
 41 
 42 /*
 43  * 堆排序(从小到大)
 44  *
 45  * 参数说明：
 46  *     a -- 待排序的数组
 47  *     n -- 数组的长度
 48  */
 49 void heapSortAsc(int* a, int n)
 50 {
 51     int i,tmp;
 52 
 53     // 从(n/2-1) --> 0逐次遍历。遍历之后，得到的数组实际上是一个(最大)二叉堆。
 54     for (i = n / 2 - 1; i >= 0; i--)
 55         maxHeapDown(a, i, n-1);
 56 
 57     // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
 58     for (i = n - 1; i > 0; i--)
 59     {
 60         // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最大的。
 61         tmp = a[0];
 62         a[0] = a[i];
 63         a[i] = tmp;
 64         // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最大堆。
 65         // 即，保证a[i-1]是a[0...i-1]中的最大值。
 66         maxHeapDown(a, 0, i-1);
 67     }
 68 }
 69 
 70 /* 
 71  * (最小)堆的向下调整算法
 72  *
 73  * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 74  *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 75  *
 76  * 参数说明：
 77  *     a -- 待排序的数组
 78  *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 79  *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 80  */
 81 void minHeapDown(int* a, int start, int end)
 82 {
 83     int c = start;            // 当前(current)节点的位置
 84     int l = 2*c + 1;        // 左(left)孩子的位置
 85     int tmp = a[c];            // 当前(current)节点的大小
 86     for (; l <= end; c=l,l=2*l+1)
 87     {
 88         // "l"是左孩子，"l+1"是右孩子
 89         if ( l < end && a[l] > a[l+1])
 90             l++;        // 左右两孩子中选择较小者
 91         if (tmp <= a[l])
 92             break;        // 调整结束
 93         else            // 交换值
 94         {
 95             a[c] = a[l];
 96             a[l]= tmp;
 97         }
 98     }
 99 }
100 
101 /*
102  * 堆排序(从大到小)
103  *
104  * 参数说明：
105  *     a -- 待排序的数组
106  *     n -- 数组的长度
107  */
108 void heapSortDesc(int* a, int n)
109 {
110     int i,tmp;
111 
112     // 从(n/2-1) --> 0逐次遍历每。遍历之后，得到的数组实际上是一个最小堆。
113     for (i = n / 2 - 1; i >= 0; i--)
114         minHeapDown(a, i, n-1);
115 
116     // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
117     for (i = n - 1; i > 0; i--)
118     {
119         // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最小的。
120         tmp = a[0];
121         a[0] = a[i];
122         a[i] = tmp;
123         // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最小堆。
124         // 即，保证a[i-1]是a[0...i-1]中的最小值。
125         minHeapDown(a, 0, i-1);
126     }
127 }
128 
129 int main()
130 {
131     int i;
132     int a[] = {20,30,90,40,70,110,60,10,100,50,80};
133     int ilen = (sizeof(a)) / (sizeof(a[0]));
134 
135     cout << "before sort:";
136     for (i=0; i<ilen; i++)
137         cout << a[i] << " ";
138     cout << endl;
139 
140     heapSortAsc(a, ilen);            // 升序排列
141     //heapSortDesc(a, ilen);        // 降序排列
142 
143     cout << "after  sort:";
144     for (i=0; i<ilen; i++)
145         cout << a[i] << " ";
146     cout << endl;
147 
148     return 0;
149 }

View Code

堆排序Java实现
实现代码(HeapSort.java)

  1 /**
  2  * 堆排序：Java
  3  *
  4  * @author skywang
  5  * @date 2014/03/11
  6  */
  7 
  8 public class HeapSort {
  9 
 10     /* 
 11      * (最大)堆的向下调整算法
 12      *
 13      * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 14      *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 15      *
 16      * 参数说明：
 17      *     a -- 待排序的数组
 18      *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 19      *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 20      */
 21     public static void maxHeapDown(int[] a, int start, int end) {
 22         int c = start;            // 当前(current)节点的位置
 23         int l = 2*c + 1;        // 左(left)孩子的位置
 24         int tmp = a[c];            // 当前(current)节点的大小
 25 
 26         for (; l <= end; c=l,l=2*l+1) {
 27             // "l"是左孩子，"l+1"是右孩子
 28             if ( l < end && a[l] < a[l+1])
 29                 l++;        // 左右两孩子中选择较大者，即m_heap[l+1]
 30             if (tmp >= a[l])
 31                 break;        // 调整结束
 32             else {            // 交换值
 33                 a[c] = a[l];
 34                 a[l]= tmp;
 35             }
 36         }
 37     }
 38 
 39     /*
 40      * 堆排序(从小到大)
 41      *
 42      * 参数说明：
 43      *     a -- 待排序的数组
 44      *     n -- 数组的长度
 45      */
 46     public static void heapSortAsc(int[] a, int n) {
 47         int i,tmp;
 48 
 49         // 从(n/2-1) --> 0逐次遍历。遍历之后，得到的数组实际上是一个(最大)二叉堆。
 50         for (i = n / 2 - 1; i >= 0; i--)
 51             maxHeapDown(a, i, n-1);
 52 
 53         // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
 54         for (i = n - 1; i > 0; i--) {
 55             // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最大的。
 56             tmp = a[0];
 57             a[0] = a[i];
 58             a[i] = tmp;
 59             // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最大堆。
 60             // 即，保证a[i-1]是a[0...i-1]中的最大值。
 61             maxHeapDown(a, 0, i-1);
 62         }
 63     }
 64 
 65     /* 
 66      * (最小)堆的向下调整算法
 67      *
 68      * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 69      *     其中，N为数组下标索引值，如数组中第1个数对应的N为0。
 70      *
 71      * 参数说明：
 72      *     a -- 待排序的数组
 73      *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 74      *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 75      */
 76     public static void minHeapDown(int[] a, int start, int end) {
 77         int c = start;            // 当前(current)节点的位置
 78         int l = 2*c + 1;        // 左(left)孩子的位置
 79         int tmp = a[c];            // 当前(current)节点的大小
 80 
 81         for (; l <= end; c=l,l=2*l+1) {
 82             // "l"是左孩子，"l+1"是右孩子
 83             if ( l < end && a[l] > a[l+1])
 84                 l++;        // 左右两孩子中选择较小者
 85             if (tmp <= a[l])
 86                 break;        // 调整结束
 87             else {            // 交换值
 88                 a[c] = a[l];
 89                 a[l]= tmp;
 90             }
 91         }
 92     }
 93 
 94     /*
 95      * 堆排序(从大到小)
 96      *
 97      * 参数说明：
 98      *     a -- 待排序的数组
 99      *     n -- 数组的长度
100      */
101     public static void heapSortDesc(int[] a, int n) {
102         int i,tmp;
103 
104         // 从(n/2-1) --> 0逐次遍历每。遍历之后，得到的数组实际上是一个最小堆。
105         for (i = n / 2 - 1; i >= 0; i--)
106             minHeapDown(a, i, n-1);
107 
108         // 从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
109         for (i = n - 1; i > 0; i--) {
110             // 交换a[0]和a[i]。交换后，a[i]是a[0...i]中最小的。
111             tmp = a[0];
112             a[0] = a[i];
113             a[i] = tmp;
114             // 调整a[0...i-1]，使得a[0...i-1]仍然是一个最小堆。
115             // 即，保证a[i-1]是a[0...i-1]中的最小值。
116             minHeapDown(a, 0, i-1);
117         }
118     }
119 
120     public static void main(String[] args) {
121         int i;
122         int a[] = {20,30,90,40,70,110,60,10,100,50,80};
123 
124         System.out.printf("before sort:");
125         for (i=0; i<a.length; i++)
126             System.out.printf("%d ", a[i]);
127         System.out.printf("\n");
128 
129         heapSortAsc(a, a.length);            // 升序排列
130         //heapSortDesc(a, a.length);        // 降序排列
131 
132         System.out.printf("after  sort:");
133         for (i=0; i<a.length; i++)
134             System.out.printf("%d ", a[i]);
135         System.out.printf("\n");
136     }
137 }

View Code

它们的输出结果：

before sort:20 30 90 40 70 110 60 10 100 50 80 
after  sort:10 20 30 40 50 60 70 80 90 100 110

posted on 2014-04-26 10:45 如果天空不死阅读(62195) 评论(22) 编辑收藏举报

刷新页面返回顶部

导航

概要

堆排序介绍

堆排序图文说明

堆排序的时间复杂度和稳定性

堆排序实现