数据结构-双向链表实现
从上海到北京的高铁一路可能要经过苏州/无锡/常州/济南/天津/北京;等我到了北京,一顿公办之后,想回上海了呢?如果使用单向链表显然回不去。聪明的人们便在每一个站都标上上一个站的站名,这样就可以反着找回原来的路了,从而回到上海。
双向链表
在单向链表的基础上添加一个指向,保存上一个节点的地址,从而可以从终点索引到起点。像这样在节点上有两个指向,一个指向前一个结点,另一个指向后一个节点,从而串联起来的数据结构称为双向链表。指向称为指针域,节点的前节点称为前驱节点,后节点称为后继节点。
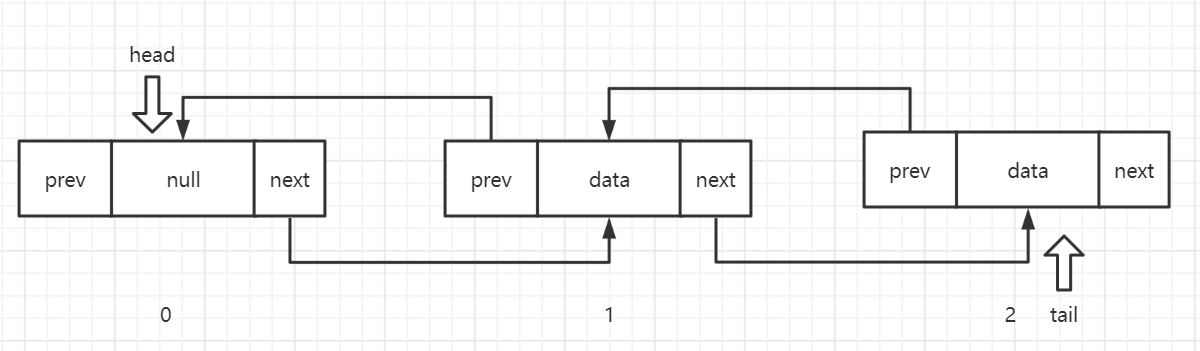
Class DoubleLinkedList<E>
属性概述
| 作用域和类型 | 属性和描述 | 备注 |
|---|---|---|
| private final Node | head 标识链表头位置 |
该属性默认一个空值节点,前驱为空,后驱为链表第一个有效节点 |
| private Node | tail 标识链表末尾 |
在链表末尾增加节点则移动该标识到最后一个节点 |
| private int | size 记录链表长度 |
添加节点 +1 删除节点 -1 |
| static final class | Node 内部节点类 |
拥有 next、prev 两个指针域和 data 数据域 |
方法概述
| 作用域和类型 | 函数和描述 | 备注 |
|---|---|---|
| public void | add(E data) 添加新值到链表 |
该节点在链表末尾添加 |
| public Object | delete(int index) 删除指定位置节点且返回节点 |
遍历到 index 位置删除 |
| public void | insert(int index, E data) 添加新值到链表指定位置 |
遍历到 index 位置删除 |
| public int | getSize() 获取链表的长度 |
返回属性 size 当前值 |
| public Object | getData(int index) 获取链表指定位置的值 |
|
| public void | print() 打印链表 |
用于调试 |
| public boolean | isEmpty() 判断链表为空 |
|
| public void clear() | clear() 清空链表数据部分 |
保留了头部节点 |
关键操作步骤
链表末尾添加元素
往链表末尾添加元素,一般分为两种情况:链表长度为空、链表长度不为空。
第一种:链表长度为空,只有一个空节点(数据域部分为空),head 和 tail 指针都指向该节点,插入节点,步骤如下:
第一步:将 head 节点的 next 指针域指向 newNode;用于找到 head 的后继节点;
第二步:将 newNode 的 prev 指针域指向 head ;用于找到 newNode 的前驱节点;
第三步:将 tail 移动到 newNode 的位置;tail 永远标记链表的末尾;

第二种: 链表长度不为空,需要在 tail 后面直接添加节点,再把 tail 节点移动到新节点;
第一步:将 末尾节点 tail 的 next 指针域指向 newNode,用于找到新节点;
第二步:将 newNode 的 prev 指针域指向 tail ,用于找到 newNode 的前驱节点;
第三步:将 tail 移动到 newNode 的位置,tail 永远标记链表的末尾;

public void add(E data) {
Node newNode = new Node(data);
if (isEmpty()) {
head.next = newNode;
newNode.prev = head;
} else {
tail.next = newNode;
newNode.prev = tail;
}
tail = newNode;
size++;
}
删除指定下标的元素
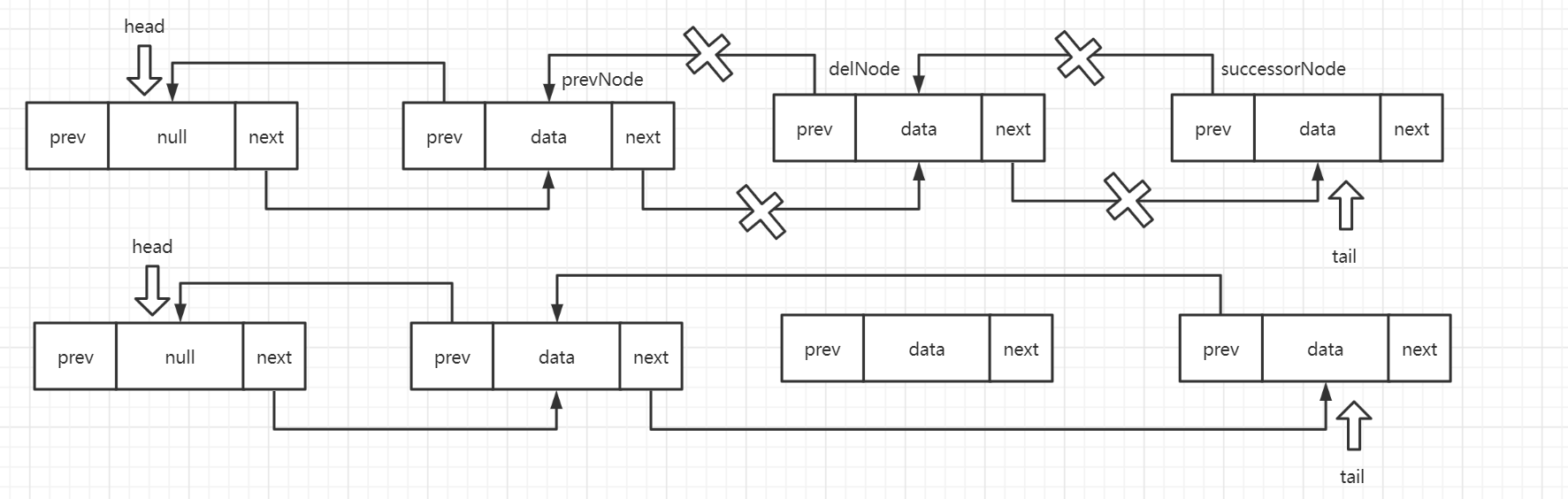
删除指定下标的元素,采用遍历方式寻找该下标对应的节点的上一个节点 prevNode,使用 next 指针域便可以找到该下标节点 delNode,该节点一般分为两种情况:指定位置是末尾节点、指定位置不是末尾节点,对应不同处理。
第一种:指定位置是末尾节点,由于是末尾节点,那么直接将 next 指针域置空即可,步骤如下:
第一步:将 prevNode 的 next 指针域置空;
第二步:移动 tail 到 prevNode,tail 永远标记链表的末尾;

第二种:指定位置不是末尾节点,需要将原来的链接剪短,重新连接,步骤如下:
第一步:获取该删除节点的后继节点 successorNode;
第二步:获取该删除节点的前驱节点的 next 指针域指向 successorNode;
第三步:将 successorNode 的 prev 指针域指向 prevNode;
public Object delete(int index) {
Node prevNode = head;
if (index > size) return null;
for (int i = 0; i < index - 1; i++) {
prevNode = prevNode.next;
}
Node delNode = prevNode.next;
if (delNode.next == null) {
prevNode.next = null;
tail = prevNode;
} else {
Node successorNode = delNode.next;
prevNode.next = successorNode;
successorNode.prev = prevNode;
}
size--;
return delNode;
}
向指定下标的添加元素
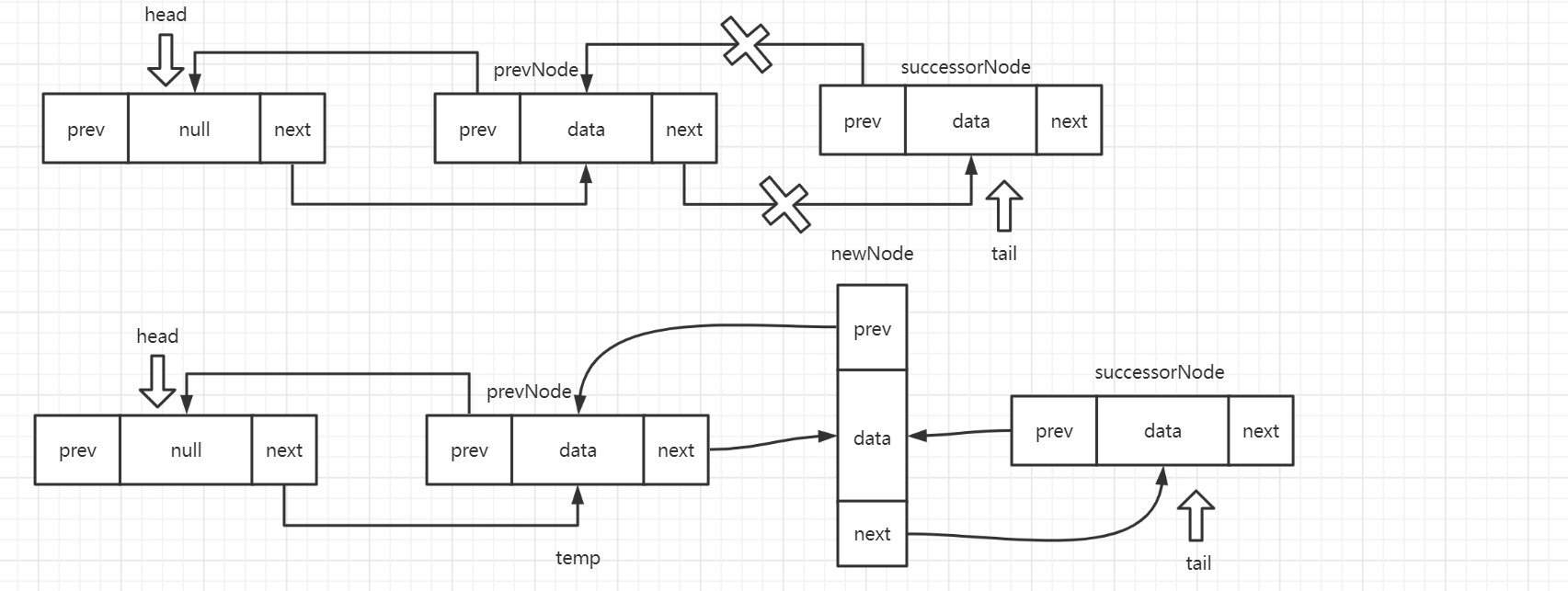
向指定下标的添加元素,采用遍历方式寻找该下标对应的节点的上一个节点 prevNode,在 prevNode 和其后继节点 successorNode 之间插入 newNode。步骤如下:
第一步:获取 prevNode 节点的后继节点 successorNode;
第二步:将 prevNode 的 next 指针域指向 newNode;
第三步:将新节点 newNode 的 prev 指针域指向 prevNode;
第四步:将后继节点 successorNode 的 prev 指针域指向 newNode;
第五步:将新节点 successorNode 的 next 指针域指向 successorNode;
public void insert(int index, E data) {
Node newNode = new Node(data);
Node prevNode = head;
if (index > size) return;
for (int i = 0; i < index - 1; i++) {
prevNode = prevNode.next;
}
Node successorNode = prevNode.next;
prevNode.next = newNode;
newNode.prev = prevNode;
successorNode.prev = newNode;
newNode.next = successorNode;
size++;
}
编码实现
interface LinkedList<E>
package com.skystep.数据结构和算法.链表.双向链表;
public interface LinkedList<E> {
//在链表尾部增加数据
void add(E data);
//删除指定位置的节点
Object delete(int index);
//在指定索引处插入节点
void insert(int index, E data);
//获取链表长度;
int getSize();
//获取某个索引数据
Object getData(int index);
void print();
//是否空
boolean isEmpty();
// 清空链表
void clear();
}
class DoubleLinkedList<E>
package com.skystep.数据结构和算法.链表.双向链表;
public class DoubleLinkedList<E> implements LinkedList<E> {
private final Node head = new Node();
private Node tail = null;
private int size = 0;
@Override
public void add(E data) {
Node newNode = new Node(data);
if (isEmpty()) {
head.next = newNode;
newNode.prev = head;
} else {
tail.next = newNode;
newNode.prev = tail;
}
tail = newNode;
size++;
}
@Override
public Object delete(int index) {
Node prevNode = head;
if (index > size) return null;
for (int i = 0; i < index - 1; i++) {
prevNode = prevNode.next;
}
Node delNode = prevNode.next;
if (delNode.next == null) {
prevNode.next = null;
tail = prevNode;
} else {
Node successorNode = delNode.next;
prevNode.next = successorNode;
successorNode.prev = prevNode;
}
size--;
return delNode;
}
@Override
public void insert(int index, E data) {
Node newNode = new Node(data);
Node prevNode = head;
if (index > size) return;
for (int i = 0; i < index - 1; i++) {
prevNode = prevNode.next;
}
Node successorNode = prevNode.next;
prevNode.next = newNode;
newNode.prev = prevNode;
successorNode.prev = newNode;
newNode.next = successorNode;
size++;
}
@Override
public int getSize() {
return size;
}
@Override
public Object getData(int index) {
Node temp = head;
if (index > size) return null;
for (int i = 0; i < index - 1; i++) {
temp = temp.next;
}
return temp.data;
}
@Override
public void print() {
Node temp = head.next;
while (temp != null) {
System.out.print(temp.data + " ");
temp = temp.next;
}
System.out.println();
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void clear() {
head.next = null;
tail = null;
size = 0;
}
static final class Node<E> {
private Node next = null;
private Node prev = null;
private E data = null;
public Node() {
}
public Node(E data) {
this.data = data;
}
public Node(Node next, Node prev, E data) {
this.next = next;
this.prev = prev;
this.data = data;
}
}
}
class Client
package com.skystep.数据结构和算法.链表.双向链表;
public class Client {
public static void main(String[] args) {
DoubleLinkedList<Integer> doubleLinkedList = new DoubleLinkedList<>();
doubleLinkedList.add(1);
doubleLinkedList.add(2);
doubleLinkedList.add(3);
doubleLinkedList.add(4);
doubleLinkedList.insert(3, 10);
System.out.println("size:" + doubleLinkedList.getSize());
doubleLinkedList.print();
doubleLinkedList.delete(4);
System.out.println("size:" + doubleLinkedList.getSize());
doubleLinkedList.print();
doubleLinkedList.clear();
System.out.println("size:" + doubleLinkedList.getSize());
doubleLinkedList.print();
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号