深度学习笔记
Python中有很多软件包可用于构建深度神经网络。
最直观的一个是scikit-neuralnetwork软件包,sknn.mlp模块即来于此
正则化可以提高神经网路的泛化,避免过度拟合。
对代价函数要进行改写,添加正则项。
添加衰减参数来惩罚较大的权重来实现
回归例子
1 from sklearn import datasets 2 3 boston = datasets.load_boston() 4 x, y = boston.data, boston.target 5 print(x, y) 6 from sklearn import preprocessing 7 8 x_MinMax = preprocessing.MinMaxScaler() 9 y_MinMax = preprocessing.MinMaxScaler() 10 import numpy as np 11 12 y = np.array(y).reshape((len(y), 1)) 13 x = x_MinMax.fit_transform(x) 14 y = y_MinMax.fit_transform(y) 15 x.mean(axis=0) # x的均值置为0 16 print(y_MinMax.scale_) 17 18 import random 19 from sklearn.model_selection import train_test_split 20 21 np.random.seed(2016) 22 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2) 23 print(len(x_train)) 24 25 from sknn.mlp import Regressor, Layer 26 27 # ==================================================================== 28 # ==================================================================== 29 fit1 = Regressor( 30 layers=[ 31 Layer('Sigmoid', units=6), 32 Layer('Sigmoid', units=14), 33 Layer('Linear')], 34 learning_rate=0.02, # 学习速率设置,要适中 35 random_state=2016, 36 n_iter=100) 37 38 print('fitting model right now') 39 fit1.fit(x_train, y_train) 40 41 pred1_train = fit1.predict(x_train) 42 from sklearn.metrics import mean_squared_error 43 44 mse_1 = mean_squared_error(pred1_train, y_train) 45 46 print('Sigmoid train error: ', mse_1) 47 48 # ==================================================================== 49 # ==================================================================== 50 # 换成ReLU激活函数 51 52 fit2 = Regressor( 53 layers=[ 54 Layer('Rectifier', units=6), 55 Layer('Rectifier', units=14), 56 Layer('Linear')], 57 learning_rate=0.02, # 学习速率设置,要适中 58 random_state=2016, 59 n_iter=100) 60 61 print('fitting model right now') 62 fit2.fit(x_train, y_train) 63 64 pred2_train = fit2.predict(x_train) 65 from sklearn.metrics import mean_squared_error 66 67 mse_2 = mean_squared_error(pred2_train, y_train) 68 69 print('ReLU train error: ', mse_2) 70 71 # ==================================================================== 72 # ==================================================================== 73 # 换成ReLU激活函数,添加正则化,减少过度拟合 74 75 fit3 = Regressor( 76 layers=[ 77 Layer('Rectifier', units=6), 78 Layer('Rectifier', units=14), 79 Layer('Linear')], 80 learning_rate=0.02, # 学习速率设置,要适中 81 random_state=2016, 82 regularize='L2', 83 weight_decay=0.001, 84 n_iter=100) 85 86 print('fitting model right now') 87 fit3.fit(x_train, y_train) 88 89 pred3_train = fit3.predict(x_train) 90 from sklearn.metrics import mean_squared_error 91 92 mse_3 = mean_squared_error(pred3_train, y_train) 93 94 print('train error: ', mse_3) 95 96 # 查看在测试样本上的表现 97 pred3_test = fit3.predict(x_test) 98 mse3_test = mean_squared_error(pred3_test, y_test) 99 print('test error: ', mse3_test) 100 for i in range(len(y_test)): 101 print(y_test[i], pred3_test[i]) 102 103 plt.scatter(y_test, pred3_test) 104 105 x = np.linspace(0, 1) 106 y = x 107 plt.plot(x, y, color='red', label='ideal case') 108 plt.xlabel("observed value") 109 plt.ylabel("predicted value") 110 # plt.title("PyPlot First Example") 111 # plt.ylim(-1.2,1.2) 112 plt.legend() 113 114 plt.show()
RESULT:
fitting model right now
Sigmoid train error: 0.0110050767582
fitting model right now
ReLU train error: 0.00583105752773
fitting model right now
train error: 0.00738282398554
test error: 0.00919026590683
[ 0.39333333] [ 0.31815418]
[ 0.26222222] [ 0.29489496]
[ 0.41111111] [ 0.48599465]
[ 0.28] [ 0.24576025]
[ 0.38666667] [ 0.32436206]
[ 0.21777778] [ 0.2463605]
[ 0.5] [ 0.35651292]
[ 0.38666667] [ 0.39062989]
[ 0.36] [ 0.30109043]
.......
测试集上性能的评估:
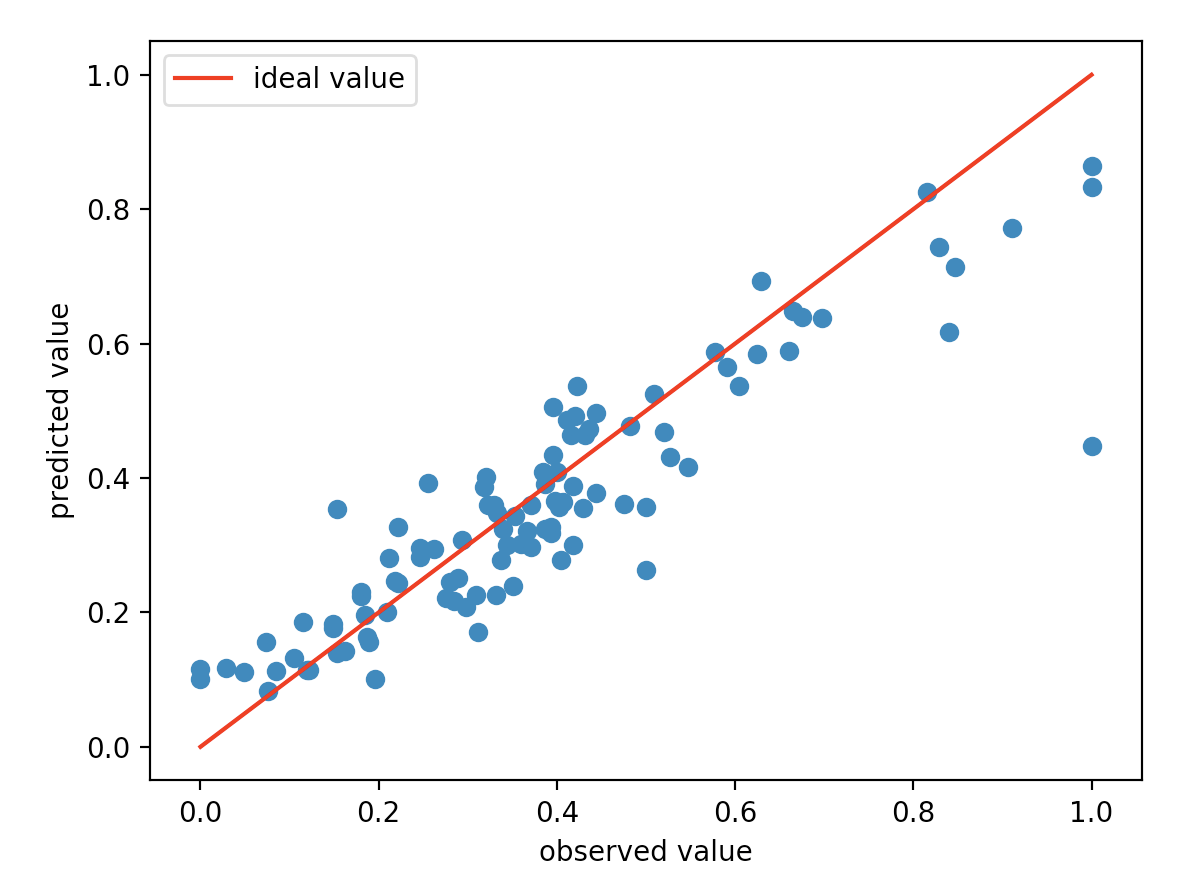
打印出相关性和R平方
from scipy.stats.stats import pearsonr correl = pearsonr(pred3_test, y_test) print('Test correlation is ', correl[0]) print('Test R^2 is ', correl[0] * correl[0])
Test correlation is [ 0.9073899]
Test R^2 is [ 0.82335643]
手写字母的分类
rmsdrop算法:对每个更新向量分量使用不同的学习速率
| 算法 | 正确率 | ||



 浙公网安备 33010602011771号
浙公网安备 33010602011771号