《算法图解》1

前三章是打基础的,后面介绍的是应用广泛的算法。书中代码均用Python 2.7编写
一、算法简介
算法是一组完成任务的指令
书中介绍算法的流程:描述算法----示例代码------大O()讨论运行时间-----可以解决的问题
要明白不同算法的 优缺点,还要知道采用不同的数据结构结果可能大不相同。所以,算法和数据结构是不分家的
二分查找:
二分查找算法:每次都可以减少一半的量,前提是列表必须有序
对于二分查找,从中间开始。这样每次就可以减少一半的量,最多需要lgN步,O(logN)。与之相对应,简单逐个查找,则最多需要N步,O(N)。
二分代码如下:

1 def binary_search(list, item):
2 low = 0
3 high = len(list)-1
4
5 while low <= high:
6 mid = int((low + high)/2)
7 guess = list[mid]
8 if guess == item:
9 return mid
10 if guess > item:
11 high = mid - 1
12 else:
13 low = mid + 1
14 return None
15
16 my_list = (1, 3, 4, 5, 7, 9, 22, 33)
17 print (binary_search(my_list, 9))
18 print (binary_search(my_list, 8))
大O表示法
大O表示法如下,一定注意括号里面的n的意义:大O表示法让你能够比较操作数(或者运行时间),它指出了算法运行时间的增速。

大O表示法数说的 是最糟糕的情形。除最糟情况下的运行时间外,还应考虑平均情况的运行时间。
几种常见的大O运行时间:

二、选择排序
主要内容 :
- 讲解最基本的数据结构:数组和链表,区分不同之处;
- 介绍选择排序。排序很重要,如二分查找,前提是有序列表。选择排序是快速排序的基石
数组,链表操作的运行时间:
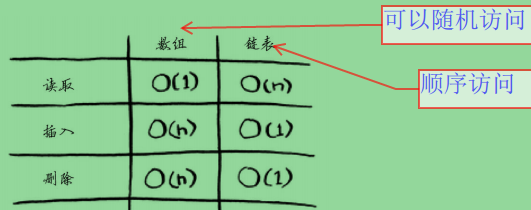
数组中的元素是相连的,而链表中的元素则可存储在内存中的任何地方
选择排序
遍历列表中的每个元素一次,每次找到最小或最大值,总时间为O(n2)
代码如下:

1 def findSmallest(arr):
2 smallest = arr[0]
3 smallest_index = 0
4 for i in range(1, len(arr)):
5 if arr[i] < smallest:
6 smallest = arr[i]
7 smallest_index = i
8 return smallest_index
9 #现在可以使用这个函数来编写选择排序算法了。
10 def selectionSort(arr):
11 newArr = []
12 for i in range(len(arr)): #代表从0到len,不包括len
13 smallest = findSmallest(arr)
14 newArr.append(arr.pop(smallest))
15 return newArr
16
17 print (selectionSort([5, 3, 6, 2, 10, -11]))
三、递归
“如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解。如何选择要看什么对你来说更重要。”
递归,是函数调用自己
基线条件与递归条件:递归条件指的是函数调用自己,而基线条件则指的是函数不再调用自己,从而避免形成无限循环。
如下图:
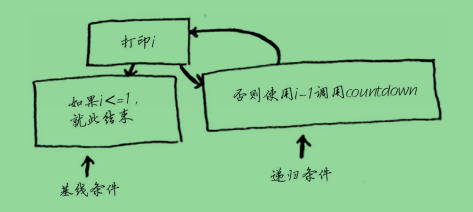
另外一种数据结构:栈,只有两种操作: 压入(插入)和弹出(删除并读取)
由下面的代码注意体会函数调用会用到栈
代码:
1 def greet(name):
2 print ("hello, " + name + "!")
3 greet2(name)
4 print ("getting ready to say bye...")
5 bye()
6
7 def greet2(name):
8 print ("how are you, " + name + "?")
9 def bye():
10 print ("ok bye!")
11
12 greet("Lin")
结果:
hello, Lin!
how are you, Lin?
getting ready to say bye...
ok bye!
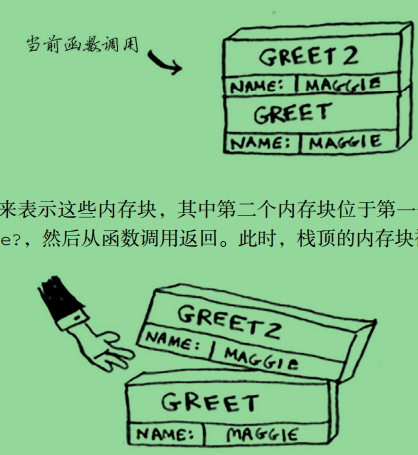
使用栈,方便,但是要付出内存的代价。






