《统计学习方法》之二：感知机学习算法

只有亲自用代码实现才算真正理解算法,有时候也要在不断的修改调试中理解，更何况只看不敲代码呢？

模型：

符号函数f(x) = sign(w*x + b)

策略：

为了求导方便，选择误分类点到超平面的总距离为损失函数，利用梯度下降进行递推 

 

代码实现：

 

% date :  2019/01/02
% author: Dufy
% 关于感知机算法
% 输入： x1,  x2数据点
%            y  为分类，1为正，-1为负

close all;
clc
clear
format compact
i=0;
a = -1;

x1=[3 4 1];
x2= [3 3 1];
y = [1 1 -1];
n = length(x1);

alpha = 1;

w= [0  0]';
b= 0;   %初值

flag = 0

while( 1 )
    
    
    for i  = 1:n
        if (y(i)*([x1(i) x2(i)] *w +b)) <= 0
            %           更新权重
            w = w+ alpha*y(i)*[x1(i) x2(i)]'
            b= b+alpha * y(i)
            
            flag = flag +1;
        end
        
    end
    
    
    if  flag==0  %分类错误点个数 = 0
        break
    end
    
    flag =0;
end

% X = ['最终的分类线为：y=',num2str(b),'x'];
% disp(X)

% 绘制wx+b=0分类线
xx=0:0.1:7;
for i=1:n
    if y(i)==1
        scatter(x1(i),x2(i),'r*')
    else
        scatter(x1(i),x2(i),'bo')
    end
    hold on
    plot(xx,(-b-w(1)*xx)/w(2),'LineWidth',4)
    %     set('fontweight','bold')
    axis equal
    axis([0, 5, 0, 5]);   % 坐标轴的显示范围
    xlabel('X1')
    ylabel('X2')
    grid on
end

 

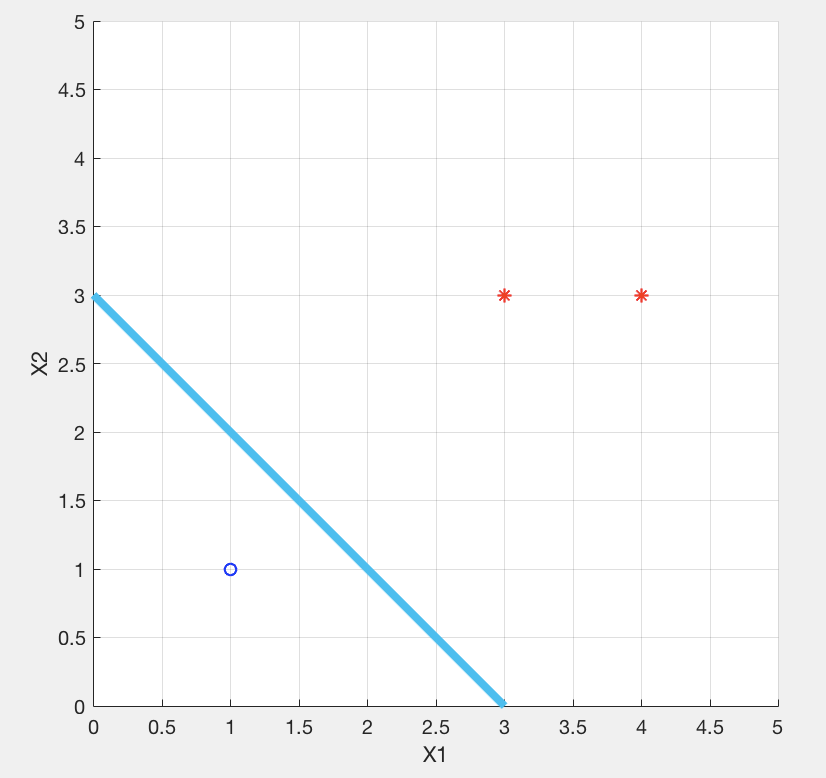
　　运行结果如下：