[NOI2018]归程
[NOI2018]归程
题目大意:
一个\(n\)个点\(m\)条边的无向连通图,每条边有两个属性\(l_i,a_i\)。\(q\)次询问,每次询问从点\(v\)出发,可以不耗费任何代价走过一段从\(v\)开始的任何一个满足\(\min\{a_i\}>p\)的路径,然后从结束的地方\(u\)走到结点\(1\),代价为\(1\sim u\)间\(l_i\)之和。求最小代价。强制在线。
数据范围:
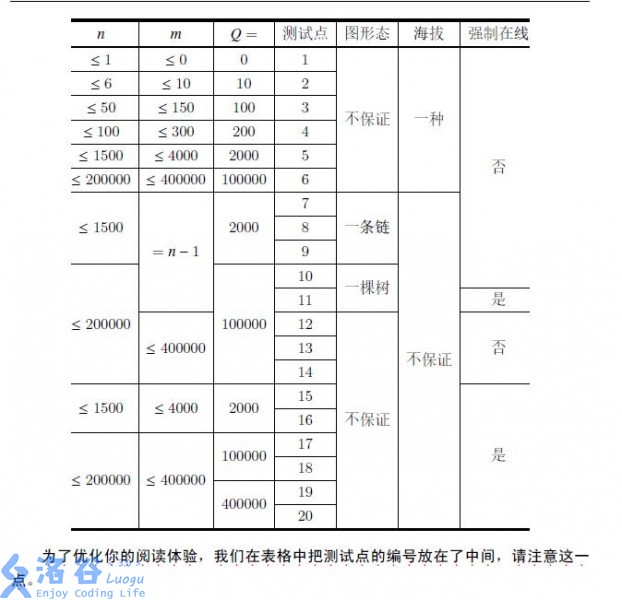
思路:
对于测试点\(1\),什么都不用做就能够拿到\(5\)分。
对于测试点\(2\sim6\),由于海拔相等,因此要么直接走到\(1\),要么完全不用走。使用Dijkstra求最短路\(dis\)即可。
对于测试点\(7\sim11\),使用树上主席树维护对应\(a_i\)的范围内深度最大的结点。令\(u\)表示\(1\sim v\)间深度最大的\(a_i\le p\)的点,则答案就是\(1\sim u\)间\(l_i\)之和。
对于测试点\(12\sim14\),将所有的边和询问按照权值从大到小排序,Kruskal维护连通性。答案就是同一连通块内\(dis\)的最小值。
对于测试点\(15\sim16\),每次重新做一遍Kruskal即可。
对于测试点\(17\sim20\),将测试点\(12\sim14\)中的并查集可持久化即可。
时间复杂度\(\mathcal O(n\log^2n)\)。
标算是一个时间复杂度\(\mathcal O(n\log n)\)的Kruskal重构树解法。
源代码:
#include<cstdio>
#include<cctype>
#include<vector>
#include<climits>
#include<algorithm>
#include<functional>
#include<ext/pb_ds/priority_queue.hpp>
inline int getint() {
register char ch;
while(!isdigit(ch=getchar()));
register int x=ch^'0';
while(isdigit(ch=getchar())) x=(((x<<2)+x)<<1)+(ch^'0');
return x;
}
const int N=2e5+1,S=1e9,M=4e5+1,Q=4e5;
struct Edge {
int to,l,a;
};
std::vector<Edge> e[N];
inline void add_edge(const int &u,const int &v,const int &l,const int &a) {
e[u].push_back((Edge){v,l,a});
e[v].push_back((Edge){u,l,a});
}
int n,m,q,k,s;
void reset() {
for(register int i=1;i<=n;i++) e[i].clear();
}
namespace subtask_same_elevation {
int elevation,dis[N];
struct Vertex {
int w,id;
bool operator > (const Vertex &rhs) const {
return w>rhs.w;
}
};
void dijkstra() {
static __gnu_pbds::priority_queue<Vertex,std::greater<Vertex> > q;
static __gnu_pbds::priority_queue<Vertex,std::greater<Vertex> >::point_iterator p[N];
for(register int i=1;i<=n;i++) {
p[i]=q.push((Vertex){dis[i]=i==1?0:INT_MAX,i});
}
while(!q.empty()) {
const int x=q.top().id;
q.pop();
for(register unsigned i=0;i<e[x].size();i++) {
const int &y=e[x][i].to,&w=e[x][i].l;
if(dis[x]+w<dis[y]) {
q.modify(p[y],(Vertex){dis[y]=dis[x]+w,y});
}
}
}
}
};
namespace subtask_tree {
int dep[N],sum[N];
class SegmentTree {
#define mid ((b+e)>>1)
private:
static const int SIZE=N*40;
struct Node {
int val,left,right;
};
Node node[SIZE];
int sz,new_node(const int &p) {
node[++sz]=node[p];
return sz;
}
public:
int root[N];
void reset() {
sz=0;
}
void insert(int &p,const int &b,const int &e,const int &x,const int &y) {
p=new_node(p);
if(dep[y]>=dep[node[p].val]) {
node[p].val=y;
}
if(b==e) return;
if(x<=mid) insert(node[p].left,b,mid,x,y);
if(x>mid) insert(node[p].right,mid+1,e,x,y);
}
int query(const int &p,const int &b,const int &e,const int &x) {
if(e==x) return node[p].val;
if(x<=mid) {
return query(node[p].left,b,mid,x);
} else {
const int u=query(node[p].left,b,mid,mid);
const int v=query(node[p].right,mid+1,e,x);
return dep[u]>dep[v]?u:v;
}
}
#undef mid
};
SegmentTree t;
void dfs(const int &x,const int &par) {
for(unsigned i=0;i<e[x].size();i++) {
const int &y=e[x][i].to,&l=e[x][i].l,&a=e[x][i].a;
if(y==par) continue;
sum[y]=sum[x]+l;
dep[y]=dep[x]+1;
t.insert(t.root[y]=t.root[x],0,S,a,y);
dfs(y,x);
}
}
};
namespace subtask_offline {
using namespace subtask_same_elevation;
struct Edge2 {
int u,v,w;
bool operator > (const Edge2 &rhs) const {
return w>rhs.w;
}
};
struct Query {
int v,p,id;
bool operator > (const Query &rhs) const {
return p>rhs.p;
}
};
int ans[Q];
Edge2 edge[M];
Query que[Q];
class DisjointSet {
private:
int anc[N],val[N];
int find(const int &x) {
return x==anc[x]?x:anc[x]=find(anc[x]);
}
public:
void init() {
for(register int i=1;i<=n;i++) {
anc[i]=i;
val[i]=dis[i];
}
}
void merge(const int &x,const int &y) {
const int p=find(x),q=find(y);
val[q]=std::min(val[q],val[p]);
anc[p]=q;
}
bool same(const int &x,const int &y) {
return find(x)==find(y);
}
int query(const int &x) {
return val[find(x)];
}
};
DisjointSet djs;
};
namespace subtask_n2 {
using namespace subtask_same_elevation;
using namespace subtask_offline;
};
namespace subtask_default {
using namespace subtask_same_elevation;
using namespace subtask_offline;
struct PersistentDisjointSet {
#define mid ((b+e)>>1)
static const int SIZE=N*40;
struct Node {
int val,left,right,size,dist;
};
Node node[SIZE];
int sz,new_node(const int &p) {
node[++sz]=node[p];
return sz;
}
int getpos(const int &p,const int &b,const int &e,const int &x) {
if(b==e) return p;
return x<=mid?getpos(node[p].left,b,mid,x):getpos(node[p].right,mid+1,e,x);
}
bool same(const int &x,const int &y) {
return node[x].val==node[y].val;
}
int root[M];
void reset() {
root[0]=0;
sz=0;
}
void build(int &p,const int &b,const int &e) {
p=new_node(p);
if(b==e) {
node[p].val=b;
node[p].size=1;
node[p].dist=dis[b];
return;
}
build(node[p].left,b,mid);
build(node[p].right,mid+1,e);
}
int find(const int &p,const int &b,const int &e,const int &x) {
const int q=getpos(p,b,e,x);
return x==node[q].val?q:find(p,b,e,node[q].val);
}
int merge2(int &p,const int &b,const int &e,const int &x,const int &y,const int &q) {
p=new_node(p);
if(b==e) {
node[p].val=y;
return p;
}
if(x<=mid) return merge2(node[p].left,b,mid,x,y,q);
if(x>mid) return merge2(node[p].right,mid+1,e,x,y,q);
return 0;
}
void merge3(int &p,const int &b,const int &e,const int &x,const int &y,const int &q) {
p=new_node(p);
if(b==e) {
node[p].size+=node[q].size;
node[p].dist=std::min(node[p].dist,node[q].dist);
return;
}
if(x<=mid) merge3(node[p].left,b,mid,x,y,q);
if(x>mid) merge3(node[p].right,mid+1,e,x,y,q);
}
void merge(int &p,const int &b,const int &e,int x,int y) {
x=find(p,b,e,x),y=find(p,b,e,y);
if(same(x,y)) return;
if(node[x].size>node[y].size) std::swap(x,y);
const int q=merge2(p,b,e,node[x].val,node[y].val,y);
merge3(p,b,e,node[y].val,node[x].val,q);
}
#undef mid
};
PersistentDisjointSet pdjs;
int hash[M];
};
int main() {
//freopen("return.in","r",stdin);
//freopen("return.out","w",stdout);
for(register int T=getint();T;T--) {
n=getint(),m=getint();
bool is_tree=m==n-1;
bool same_elevation=true;
for(register int i=0;i<m;i++) {
const int u=getint(),v=getint(),l=getint(),a=getint();
subtask_offline::edge[i]=(subtask_offline::Edge2){u,v,a};
if(i!=0&&subtask_same_elevation::elevation!=a) same_elevation=false;
add_edge(u,v,l,subtask_same_elevation::elevation=a);
}
q=getint(),k=getint(),s=getint();
bool offline=k==0;
if(q==0) {
//point 1
goto Next;
}
if(same_elevation&&offline) {
//point 2~6
using namespace subtask_same_elevation;
dijkstra();
for(register int i=0;i<q;i++) {
const int v=getint(),p=getint();
printf("%d\n",p<elevation?0:dis[v]);
}
goto Next;
}
if(is_tree) {
//point 7~11
using namespace subtask_tree;
dfs(1,0);
for(register int i=0,ans=0;i<q;i++) {
const int v=(getint()+k*ans-1)%n+1;
const int p=(getint()+k*ans)%(s+1);
printf("%d\n",ans=sum[t.query(t.root[v],0,S,p)]);
}
t.reset();
goto Next;
}
if(offline) {
//point 12~14
using namespace subtask_offline;
dijkstra();
std::sort(&edge[0],&edge[m],std::greater<Edge2>());
for(register int i=0;i<q;i++) {
const int v=getint(),p=getint();
que[i]=(Query){v,p,i};
}
std::sort(&que[0],&que[q],std::greater<Query>());
djs.init();
for(register int i=0,j=0;j<q;j++) {
for(;edge[i].w>que[j].p;i++) {
const int &u=edge[i].u,&v=edge[i].v;
if(djs.same(u,v)) continue;
djs.merge(u,v);
}
ans[que[j].id]=djs.query(que[j].v);
}
for(register int i=0;i<q;i++) {
printf("%d\n",ans[i]);
}
goto Next;
}
if(n<=1500&&m<=4000&&q<=2000) {
//point 15~16
using namespace subtask_n2;
dijkstra();
for(register int i=0,last=0;i<q;i++) {
const int v=(getint()+k*last-1)%n+1;
const int p=(getint()+k*last)%(s+1);
djs.init();
for(register int i=0;i<m;i++) {
if(edge[i].w<=p) continue;
const int &u=edge[i].u,&v=edge[i].v;
if(djs.same(u,v)) continue;
djs.merge(u,v);
}
printf("%d\n",last=djs.query(v));
}
goto Next;
}
//point 17~20
using namespace subtask_default;
dijkstra();
pdjs.build(pdjs.root[0],1,n);
std::sort(&edge[0],&edge[m],std::greater<Edge2>());
for(register int i=0;i<m;i++) {
hash[i+1]=edge[i].w;
const int &u=edge[i].u,&v=edge[i].v;
pdjs.merge(pdjs.root[i+1]=pdjs.root[i],1,n,u,v);
}
for(register int i=0,last=0;i<q;i++) {
const int v=(getint()+k*last-1)%n+1;
const int p=(getint()+k*last)%(s+1);
const int pos=std::lower_bound(&hash[1],&hash[m]+1,p,std::greater<int>())-&hash[1];
printf("%d\n",last=pdjs.node[pdjs.find(pdjs.root[pos],1,n,v)].dist);
}
pdjs.reset();
Next:
reset();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号