java--二叉树解析及基本实现
一.二叉树的结构
在进行链表结构开发的过程之中,会发现所有的数据按照首尾相连的状态进行保存,那么 在进行数据查询时为了判断数据是否存在,这种情况下它所面对的时间复杂度就是"O(n)",如果说它现在的数据量比较小(<30)是不会对性能造成什么影响的,而一旦保存的数据量很大,这个时候时间复杂度就会严重损耗程序的运行性能,那么对于数据的存储结构就必须发生改变,应该尽可能的减少检索次数为出发点进行设计.对于现在的数据结构而言,最好的性能就是"O(logn)",现在想要实现它,就可以使用二叉树的结构来完成.
如果想要实现一颗树结构的定义,那么就需要去考虑数据的存储形式,在二叉树的实现中,基本原理如下:取第一个保存的数据为根节点,当比根节点小或相等的数据需要放在根的左子树,而大于节点的数据要放在该节点的右子树.同时,在每一个树节点中需要保存的东西有如下:父节点,数据,左子树,右子树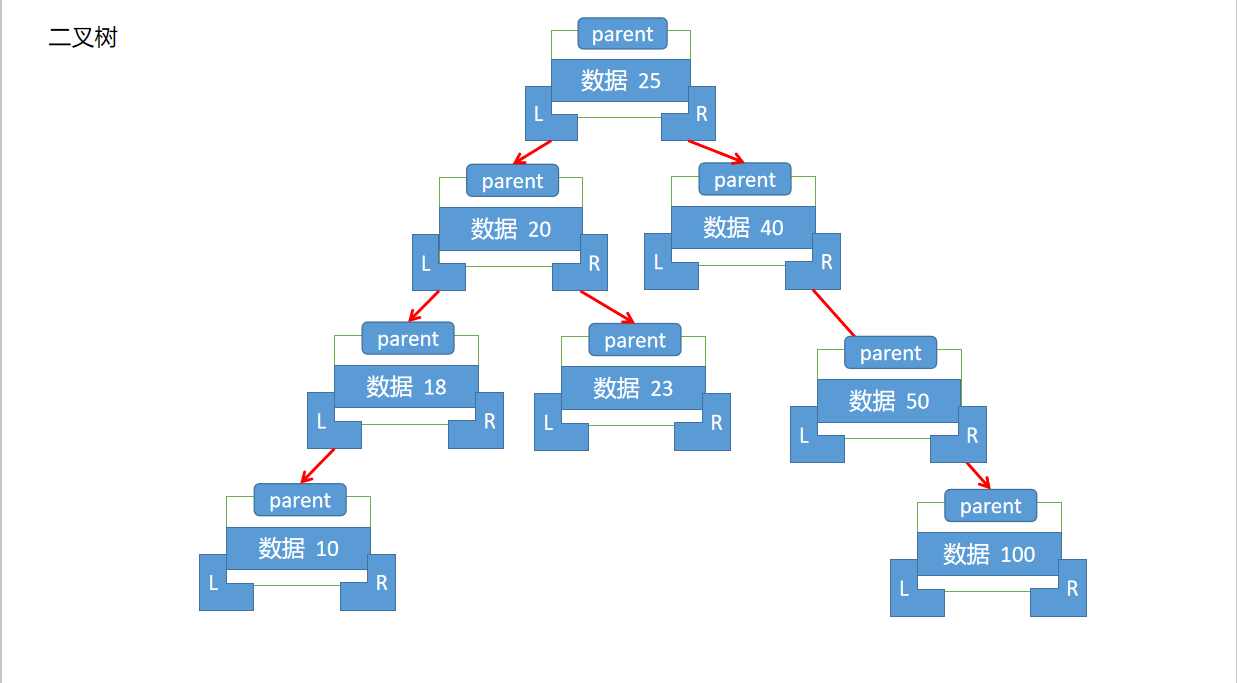
--当要进行数据检索时,此时就需要进行每个节点的判断,例如现在我们要查找数据23,那么我们可以知道23比25小,那么查询25的左子树,而25的左子树为20比数据23小,则查询他的右子树,其右子树23就是我们所需要的数据.其时间复杂度为O(logn).
--对于二叉树的查询,也有三种形式,分别为:前序遍历(根-左-右),中序遍历(左-根-右),后序遍历(左-右-根),以中序遍历为例,则以上的数据在中序遍历的时候最终的结果就是(10,18,20,23,25,40,50,100),可以发现二叉树中的内容全部都是排序的结果.
二.二叉树的基础实现
二叉树实现的关键问题在于数据的保存,而且数据由于牵扯到对象比较的问题,那么一定要有比较器的支持,而首选的比较器就是Comparable,以Person数据为例:
1 package 常用类库.二叉树的实现;
2
3 import javax.jws.Oneway;
4 import java.lang.reflect.Array;
5 import java.util.Arrays;
6
7 /**
8 * @author : S K Y
9 * @version :0.0.1
10 */
11 class Person implements Comparable<Person> {
12 private String name;
13 private int age;
14
15 public Person() {
16 }
17
18 public Person(String name, int age) {
19 this.name = name;
20 this.age = age;
21 }
22
23 public String getName() {
24 return name;
25 }
26
27 public void setName(String name) {
28 this.name = name;
29 }
30
31 public int getAge() {
32 return age;
33 }
34
35 public void setAge(int age) {
36 this.age = age;
37 }
38
39 @Override
40 public int compareTo(Person o) {
41 return this.age - o.age;
42 }
43
44 @Override
45 public String toString() {
46 return "Person{" +
47 "name='" + name + '\'' +
48 ", age=" + age +
49 '}';
50 }
51 }
52
53 class BinaryTree<T extends Comparable<T>> {
54 private class Node {
55 private Comparable<T> data; //存放Comparable,可以比较大小
56 private Node parent; //存放父节点
57 private Node left; //保存左子树
58 private Node right; //保存右子树
59
60 public Node(Comparable<T> data) { //构造方式直接实现数据的存储
61 this.data = data;
62 }
63
64 /**
65 * 实现节点数据的适当位置的存储
66 *
67 * @param newNode 创建的新节点
68 */
69 void addNode(Node newNode) {
70 if (newNode.data.compareTo((T) this.data) <= 0) { //比当前的节点小
71 if (this.left == null) { //没有左子树,进行保存
72 this.left = newNode;
73 newNode.parent = this; //保存父节点
74 } else { //需要向左边继续判断
75 this.left.addNode(newNode); //继续向下判断
76 }
77 } else { //比根节点的数据要大
78 if (this.right == null) { //没有右子树
79 this.right = newNode;
80 newNode.parent = this; //保存父节点
81 } else {
82 this.right.addNode(newNode); //继续向下进行
83 }
84 }
85 }
86
87 /**
88 * 实现所有数据的获取处理,按照中序遍历的形式来完成
89 */
90 void toArrayNode() {
91 if (this.left != null) { //存在左子树
92 this.left.toArrayNode(); //递归调用
93 }
94 BinaryTree.this.returnData[BinaryTree.this.foot++] = this.data;
95 if (this.right != null) {
96 this.right.toArrayNode();
97 }
98 }
99
100 }
101
102 /*===========以下是二叉树的功能实现=============*/
103 private Node root; //保存的根节点
104 private int count; //保存数据个数
105 private Object[] returnData; //返回的数据
106 private int foot = 0; //脚标控制
107
108 /**
109 * 进行数据的增加
110 *
111 * @param data 需要保存的数据
112 * @throws NullPointerException 保存的数据不允许为空
113 */
114 public void add(Comparable<T> data) {
115 if (data == null) {
116 throw new NullPointerException("保存的数据不允许为空");
117 }
118 //所有的数据本身不具备有节点关系的匹配,那么一定要将其包装在Node类之中
119 Node newNode = new Node(data); //保存节点
120 if (this.root == null) { //表名此时没有根节点,那么第一个保存的数据将作为根节点
121 this.root = newNode;
122 } else { //需要将其保存到一个合适的节点
123 this.root.addNode(newNode);
124 }
125 count++;
126 }
127
128
129 /**
130 * 以对象数组的形式返回数据,如果没有数据则返回null
131 *
132 * @return 全部数据
133 */
134 public Object[] toArray() {
135 if (this.count == 0) return null;
136 this.foot = 0; //脚标清零
137 this.returnData = new Object[count];
138 this.root.toArrayNode();
139 return returnData;
140 }
141
142 }
143
144 public class MyBinaryTree {
145 public static void main(String[] args) {
146 BinaryTree<Person> tree = new BinaryTree<>();
147 tree.add(new Person("小红", 20));
148 tree.add(new Person("小光", 80));
149 tree.add(new Person("小亮", 40));
150 tree.add(new Person("小龙", 25));
151 tree.add(new Person("小C", 77));
152 tree.add(new Person("小D", 66));
153 tree.add(new Person("小九", 35));
154 tree.add(new Person("小Q", 54));
155 Object[] objects = tree.toArray();
156 System.out.println(Arrays.toString(objects));
157 }
158 }
--运行结果
[Person{name='小红', age=20}, Person{name='小龙', age=25}, Person{name='小九', age=35}, Person{name='小亮', age=40}, Person{name='小Q', age=54}, Person{name='小D', age=66}, Person{name='小C', age=77}, Person{name='小光', age=80}]
Process finished with exit code 0
--在以上的代码实现中采用了递归算法的操作,采用递归算法,相对而言其代码更加的简介明了,但是此时在进行数据添加的时候,只是实现了节点关系的保存,而这种关系保存后的结果就是所有的数据都是有序排列的.
三.数据删除
二叉树的数据删除操作是非常复杂的,因为在进行数据删除的时候需要考虑的情况是比较多的:
--1.如果删除的节点没有子节点,那么直接删除该节点即可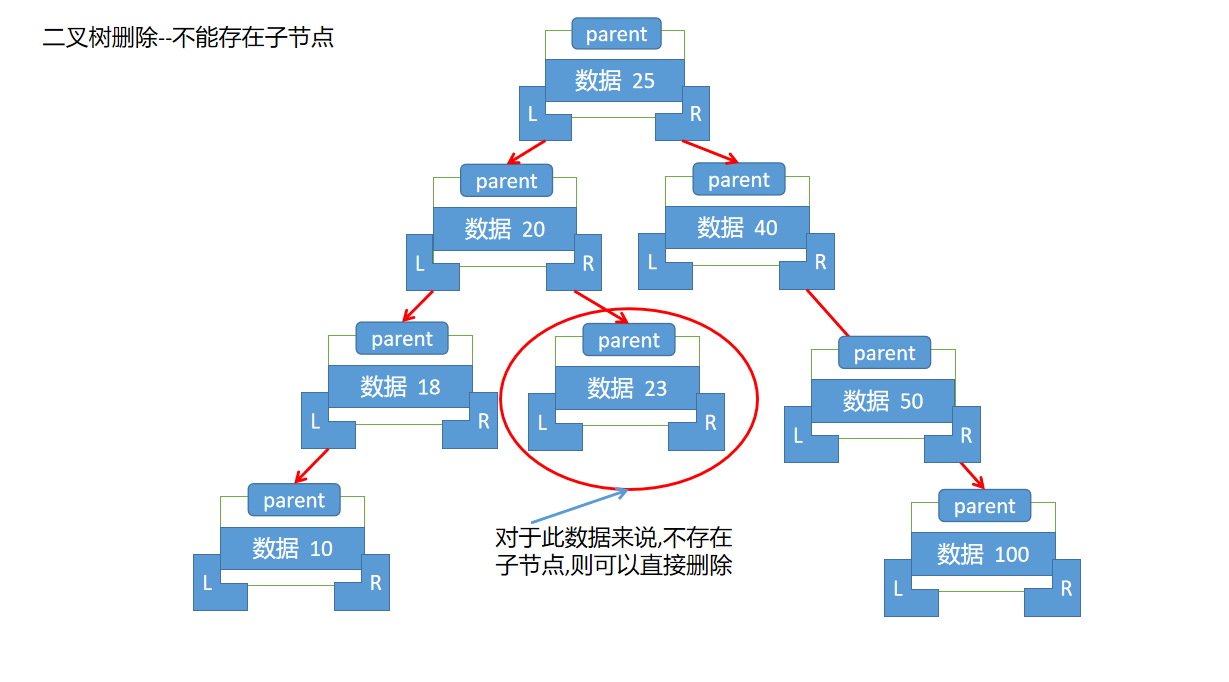
--2.如果待删除节点只有一个子节点,那么删除该节点之后,考虑两种情况的分析:
a.只有一个左子树:将其左子树放置于原来父节点的位置
b.只有一个右子树:也是将其右子树放置于原来父节点的位置
--3.如果删除节点存在两个子节点,那么删除该节点,首先需要找到当前节点的后继节点,这个后继节点就是其右子树的左侧叶子节点(及该节点下的最后一个左子树)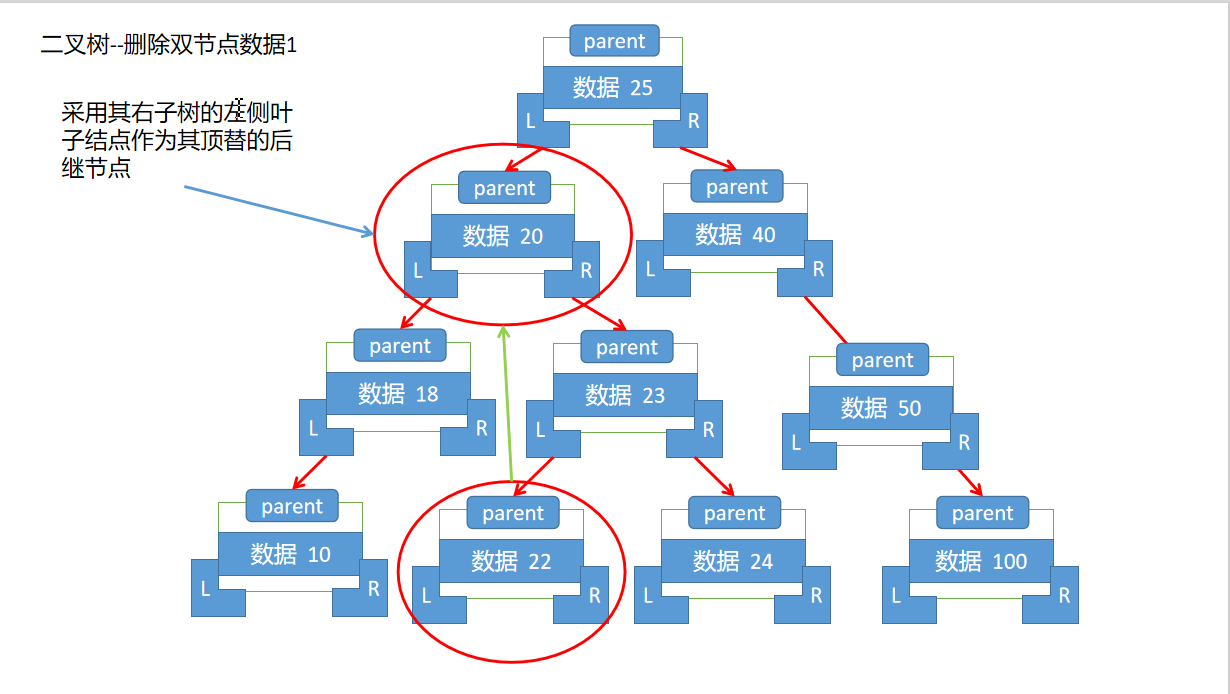
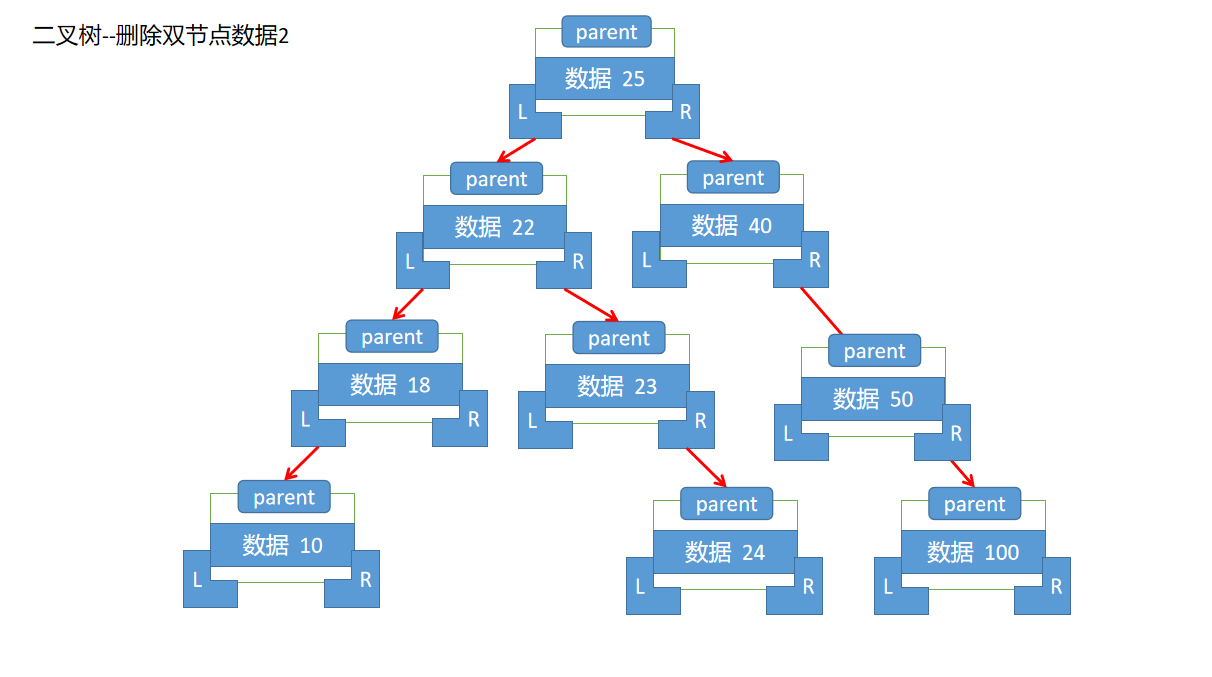
--具体的代码实现
1 package 常用类库.二叉树的实现;
2
3 import java.util.Arrays;
4
5 /**
6 * @author : S K Y
7 * @version :0.0.1
8 */
9 class Person implements Comparable<Person> {
10 private String name;
11 private int age;
12
13 public Person() {
14 }
15
16 public Person(String name, int age) {
17 this.name = name;
18 this.age = age;
19 }
20
21 public String getName() {
22 return name;
23 }
24
25 public void setName(String name) {
26 this.name = name;
27 }
28
29 public int getAge() {
30 return age;
31 }
32
33 public void setAge(int age) {
34 this.age = age;
35 }
36
37 @Override
38 public int compareTo(Person o) {
39 return this.age - o.age;
40 }
41
42 @Override
43 public String toString() {
44 return "Person{" +
45 "name='" + name + '\'' +
46 ", age=" + age +
47 '}';
48 }
49 }
50
51 class BinaryTree<T extends Comparable<T>> {
52 private class Node {
53 private Comparable<T> data; //存放Comparable,可以比较大小
54 private Node parent; //存放父节点
55 private Node left; //保存左子树
56 private Node right; //保存右子树
57
58 public Node(Comparable<T> data) { //构造方式直接实现数据的存储
59 this.data = data;
60 }
61
62 /**
63 * 实现节点数据的适当位置的存储
64 *
65 * @param newNode 创建的新节点
66 */
67 void addNode(Node newNode) {
68 if (newNode.data.compareTo((T) this.data) <= 0) { //比当前的节点小
69 if (this.left == null) { //没有左子树,进行保存
70 this.left = newNode;
71 newNode.parent = this; //保存父节点
72 } else { //需要向左边继续判断
73 this.left.addNode(newNode); //继续向下判断
74 }
75 } else { //比根节点的数据要大
76 if (this.right == null) { //没有右子树
77 this.right = newNode;
78 newNode.parent = this; //保存父节点
79 } else {
80 this.right.addNode(newNode); //继续向下进行
81 }
82 }
83 }
84
85 /**
86 * 实现所有数据的获取处理,按照中序遍历的形式来完成
87 */
88 void toArrayNode() {
89 if (this.left != null) { //存在左子树
90 this.left.toArrayNode(); //递归调用
91 }
92 System.out.println(foot + " " + this.data + " parent:" + this.parent + " left:" + this.left + " right:" + this.right);
93 BinaryTree.this.returnData[BinaryTree.this.foot++] = this.data;
94 if (this.right != null) {
95 this.right.toArrayNode();
96 }
97 }
98
99 @Override
100 public String toString() {
101 return "Node{" +
102 "data=" + data +
103 '}';
104 }
105 }
106
107 /*===========以下是二叉树的功能实现=============*/
108 private Node root; //保存的根节点
109 private int count; //保存数据个数
110 private Object[] returnData; //返回的数据
111 private int foot = 0; //脚标控制
112
113 /**
114 * 进行数据的增加
115 *
116 * @param data 需要保存的数据
117 * @throws NullPointerException 保存的数据不允许为空
118 */
119 public void add(Comparable<T> data) {
120 if (data == null) {
121 throw new NullPointerException("保存的数据不允许为空");
122 }
123 //所有的数据本身不具备有节点关系的匹配,那么一定要将其包装在Node类之中
124 Node newNode = new Node(data); //保存节点
125 if (this.root == null) { //表名此时没有根节点,那么第一个保存的数据将作为根节点
126 this.root = newNode;
127 } else { //需要将其保存到一个合适的节点
128 this.root.addNode(newNode);
129 }
130 count++;
131 }
132
133 /**
134 * 返回树中当前的节点,如果存在
135 *
136 * @param data 所需要在树中获取节点的对象
137 * @return 书中的当前节点, 如果不存在, 则返回null
138 */
139 private Node getNode(Comparable<T> data) {
140 Node compareNode = BinaryTree.this.root; //当前比较的Node节点
141 int i; //当前的比较结果
142 while ((i = data.compareTo((T) compareNode.data)) != 0) {
143 if (i < 0) { //当前节点比此节点小
144 compareNode = compareNode.left;
145 } else { //当前节点比此节点大
146 compareNode = compareNode.right;
147 }
148 if (compareNode == null) return null; //不存在此节点,跳出循环,说明未找到数据
149 }
150 return compareNode;
151 }
152
153 /**
154 * 判断当前节点是否存在
155 *
156 * @param data 需要判断的加节点
157 * @return 如果当前节点存在则返回true, 不存在则返回false
158 * @throws NullPointerException 查询的数据不允许为空
159 */
160 public boolean contains(Comparable<T> data) {
161 if (data == null) return false; //当前对象为空
162 if (this.count == 0) return false; //当前不存在数据
163 return getNode(data) != null;
164 }
165
166
167 /**
168 * 执行节点的删除处理
169 *
170 * @param data 需要删除的节点数据
171 */
172 public void remove(Comparable<T> data) {
173 if (this.contains(data)) { //要删除的数据存在
174 //首先需要找到要删除的节点
175 Node removeNode = this.getNode(data);
176 if (removeNode.left == null && removeNode.right == null) { //情况1:当前节点不存在子节点
177 //此时只要断开该删除节点的连接即可
178 if (removeNode.equals(removeNode.parent.left)) {
179 removeNode.parent.left = null;
180 } else {
181 removeNode.parent.right = null;
182 }
183 removeNode.parent = null; //断开删除节点的引用
184 } else if (removeNode.left == null) { //此时说明只存在right子树
185 if (removeNode.equals(removeNode.parent.left)) {
186 removeNode.parent.left = removeNode.right;
187 } else {
188 removeNode.parent.right = removeNode.right;
189 }
190 removeNode.right.parent = removeNode.parent;
191 removeNode.parent = null;
192 } else if (removeNode.right == null) { //此时说明只存在left子树
193 if (removeNode.equals(removeNode.parent.left)) {
194 removeNode.parent.left = removeNode.left;
195 } else {
196 removeNode.parent.right = removeNode.left;
197 }
198 removeNode.left.parent = removeNode.parent;
199 removeNode.parent = null;
200 } else { //两边都有节点
201 Node needMoveNode = removeNode.right; //所需移动的节点
202 System.out.println("needMoveNode: " + needMoveNode.data);
203 while (needMoveNode.left != null) {
204 needMoveNode = needMoveNode.left;
205 } //此时已经获取删除节点的最小左节点,需要将其替代原来的节点
206 //考虑删除节点的右节点不存在左节点的情况,及删除节点的右节点就是最终的needMoveNode
207 if (needMoveNode.equals(needMoveNode.parent.right)) {
208 needMoveNode.parent.right = needMoveNode.right;
209 } else {
210 needMoveNode.parent.left = needMoveNode.right;
211 }
212 //替换节点的数据内容
213 removeNode.data = needMoveNode.data;
214 //断开needMoveNode的连接
215 needMoveNode.parent = null;
216
217 }
218 this.count--;
219 }
220 }
221
222 /**
223 * 以对象数组的形式返回数据,如果没有数据则返回null
224 *
225 * @return 全部数据
226 */
227 public Object[] toArray() {
228 if (this.count == 0) return null;
229 this.foot = 0; //脚标清零
230 System.out.println("count: " + count);
231 this.returnData = new Object[count];
232 this.root.toArrayNode();
233 return returnData;
234 }
235
236 }
237
238 public class MyBinaryTree {
239 public static void main(String[] args) {
240 //为了验证算法结构的准确性,将其内容设置为与图示相同
241 BinaryTree<Person> tree = new BinaryTree<>();
242 tree.add(new Person("小红", 25));
243 tree.add(new Person("小光", 20));
244 tree.add(new Person("小亮", 40));
245 tree.add(new Person("小龙", 18));
246 tree.add(new Person("小C", 23));
247 tree.add(new Person("小D", 50));
248 tree.add(new Person("小九", 10));
249 tree.add(new Person("小Q", 22));
250 tree.add(new Person("小Q", 24));
251 tree.add(new Person("小Q", 100));
252 Object[] objects = tree.toArray();
253 System.out.println(Arrays.toString(objects));
254 //删除23节点
255 System.out.println("=======删除22节点========");
256 tree.remove(new Person("小Q", 22));
257 System.out.println(Arrays.toString(tree.toArray()));
258 System.out.println("=======删除18节点========");
259 tree.add(new Person("小Q", 22));
260 tree.remove(new Person("小龙", 18));
261 System.out.println(Arrays.toString(tree.toArray()));
262 System.out.println("=======删除50节点========");
263 tree.add(new Person("小龙", 18));
264 tree.remove(new Person("小D", 50));
265 System.out.println(Arrays.toString(tree.toArray()));
266 System.out.println("=======删除23节点========");
267 tree.add(new Person("小D", 50));
268 tree.remove(new Person("小C", 23));
269 System.out.println(Arrays.toString(tree.toArray()));
270 System.out.println("=======删除20节点========");
271 tree.add(new Person("小C", 23));
272 tree.remove(new Person("小光", 20));
273 System.out.println(Arrays.toString(tree.toArray()));
274 System.out.println("=======删除25根节点========");
275 tree.add(new Person("小光", 20));
276 tree.remove(new Person("小红", 25));
277 System.out.println(Arrays.toString(tree.toArray()));
278 }
279 }
--可以发现这种树结构的删除操作是非常繁琐的,所以如果不是必须的情况下不建议使用删除



