A RECURRENT NEURAL NETWORK WITHOUT CHAOS
本篇文章的介绍了一个非常简单的门限RNN(gated recurrent neural network),
这里有两扇门horizontal/forget gate和vertical/input gate， 即
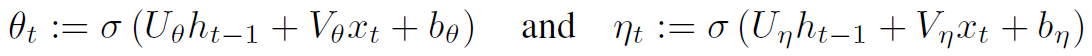
其中 
（logistic sigmoid function）
下面假设输入数据xt满足如下性质，
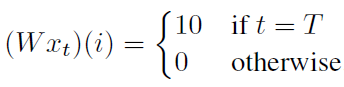
若隐层节点初始化为0， 即
，则网络对脉冲xt的响应为，
其中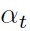
衰减到0， forget gate
控制了衰减速度，所以当隐层节点ht(i)遇到比较强的信号，ht(i)被激活，接着衰减到0，直到下一次再次被激活。
zero input比较
本文的模型，只有一个吸引子， zero state, 但其它的模型，i.e., vanilla RNN, the LSTM and the GRU 具有混沌动力学行为。
接着文章想说明，这个没有混沌的RNN在word level language modeling task也能达到很好的效果，间接的说明混沌性质并不能解释这些模型在tasks上的成功。
CHAOS IN RECURRENT NEURAL NETWORKS
考虑下面的离散动力系统， 向量u属于Rd
形成的轨迹，会进入该系统的吸引子（不变集）， 通常是分形的。
所有的RNN可以写成下面的形式
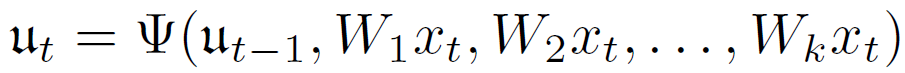
假设没有输入，则RNN可以诱导出相应的动力系统
从而刻画了产生复杂轨迹的能力。
如何才能出现上面的动力系统的行为呢？实际上是可以存在的，由于参数Wj是通过学习得到的，当遇到一个不怎么重要的数据点xt0，与隐层节点具有很弱的耦合性， 也就是说数据的影响不大， i.e., Wjxt0 ≈ 0，，就会在接下来的一段时间出现上述动力系统的行为，直到遇到一个非常重要的信号。
CHAOTIC BEHAVIOR OF LSTM AND GRU IN THE ABSENCE OF INPUT DATA
考虑下面LSTM诱导的动力系统，
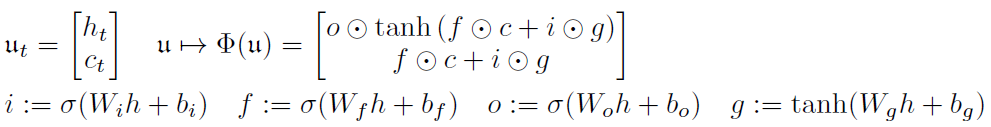
其中的参数具体为，
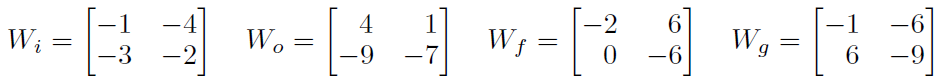
接着初始化隐层节点，
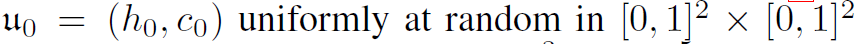
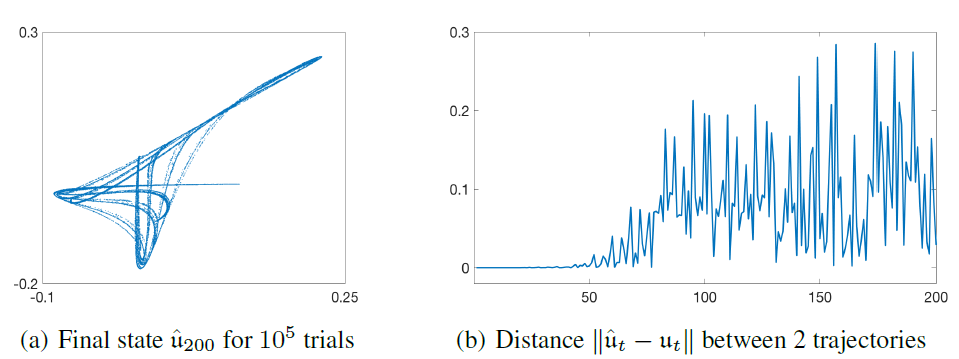
图1为具体的动力系统的展示， 图中的吸引子实质上是4维动力系统在2维上的投影。
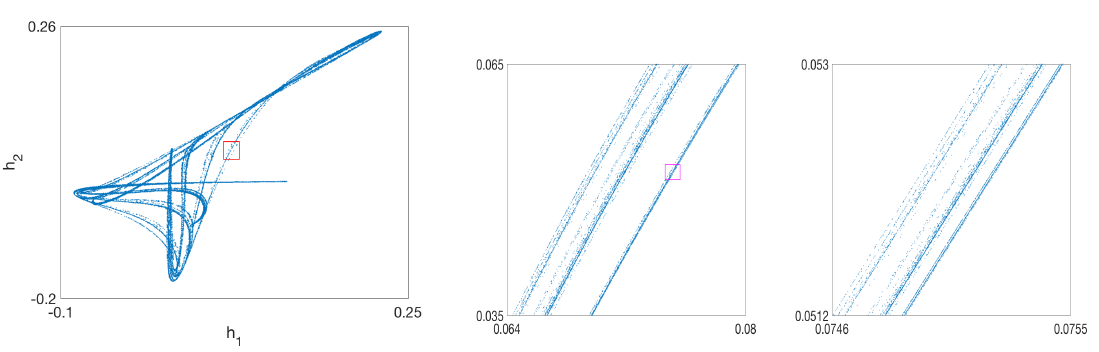
混沌动力系统具有初值敏感性，给定一个初始点，作者在[1e-7, 1e7]范围内进行扰动，跑200steps, 总共100,000次扰动。结果就是，第200步的点，几乎充满了整个吸引子。
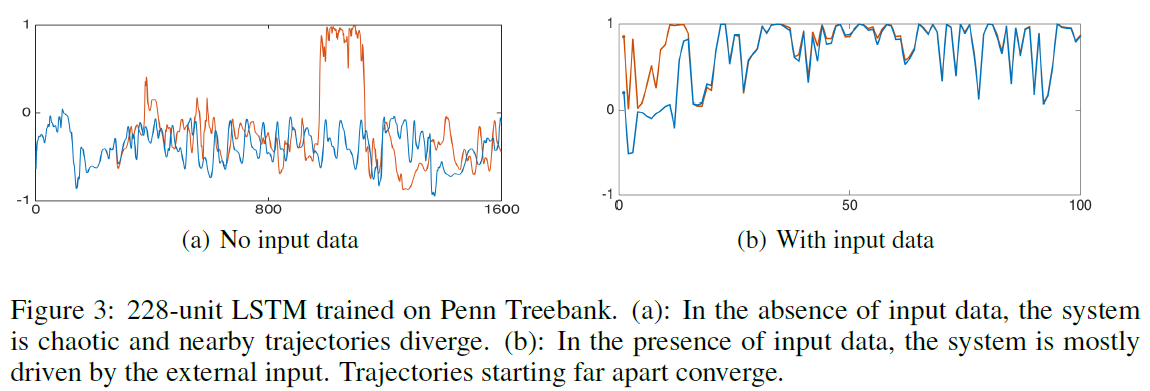
上面都是构造的例子，下面是作者在Penn Treebank corpus without dropout 训练好的LSTM，结果也出现混沌现象。当有初入的时候，就不再是一个自治的动力系统了，完全收到输入信号控制。
CHAOS-FREE BEHAVIOR OF THE CFN
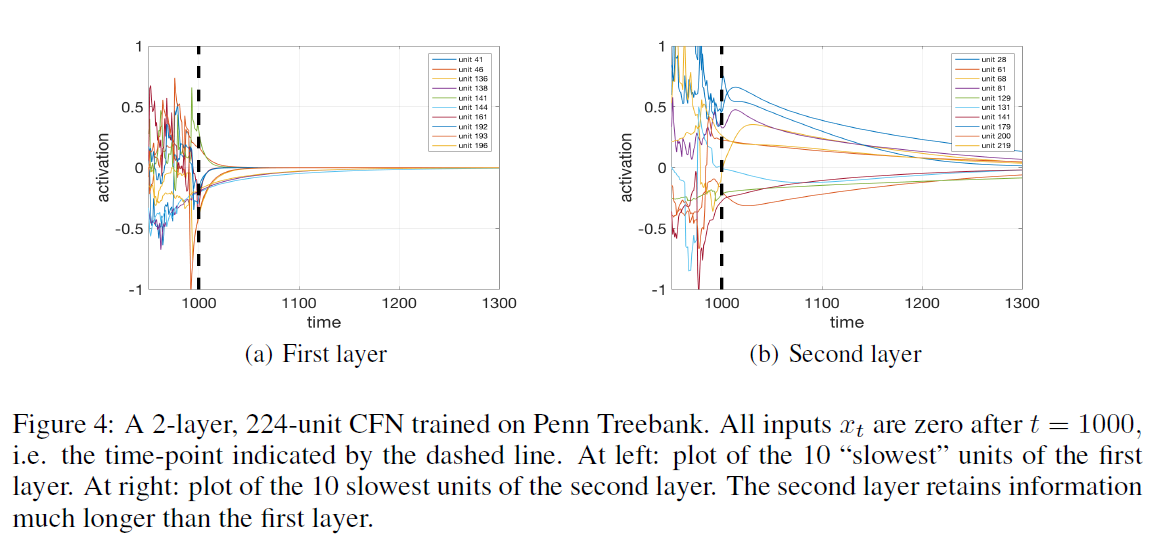
实验结果：高层的隐层节点的信号衰减慢
