Reservoir Computing: Harnessing a Universal Dynamical System
原文连接:https://sinews.siam.org/Details-Page/reservoir-computing-harnessing-a-universal-dynamical-system
目前人们对开发用于处理海量数据集的人工智能算法非常感兴趣,通常用于分类任务,例如识别照片中的面部。但是,如果我们的目标是学习一个确定性的动力系统呢?相关应用包括预测天气,控制复杂的动力系统,以及指纹识别射频发射器以保护物联网。
训练“通用”动力系统来预测所需系统的动力学是解决这个问题的一种方法,非常适合于水库计算(RC):一种用于处理时间相关信息的循环人工神经网络(见图1)。它可以在许多模式下操作,包括预测模式,上述任务。虽然研究人员已经研究了RCs超过20年[1]并成功应用于各种任务[2],但仍有许多开放性问题,动力系统社区可能会感兴趣并能够解决。
RC与传统的前馈神经网络的区别在于以下特性:
- 每个网络节点都具有不同的动态行为
- 信号的时间延迟可能沿着网络链路发生
- 网络的隐藏部分具有循环连接
- 输入和内部权重是固定的并随机选择
- 在训练期间仅调整输出权重。(加速训练)
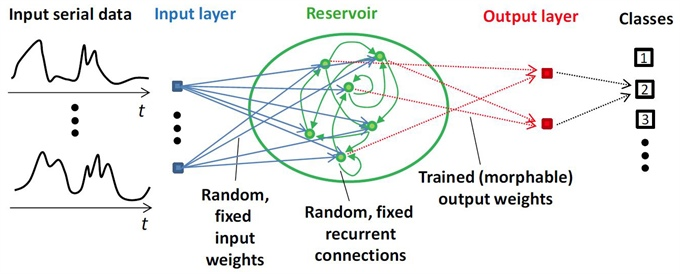
Figure 1.. Illustration of the reservoir computer architecture. Figure credit: Daniel J. Gauthier.
数学上,RC由一组自治的,时滞微分方程描述
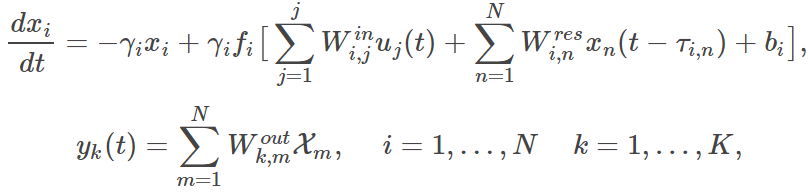
非线性函数f通常是S形的,我们可以采用开关阈值(布尔)函数的极限,如在传统的Hopfield网络中所做的那样。储层将J维输入数据流映射到更高维度的相空间 - 维度扩展
对于预测任务,我们使用有限持续时间的“训练”数据样本调整权重Wout,以便得到的输出以最小二乘意义表示输入数据。训练之后,输入信号断开,输出连接到输入以开始预测阶段。
更详细地,通过在时间Ttrain上注入输入训练数据集U并在该间隔上观察网络动态X来确定Wout。基于这些观察,我们修改权重以将输出YY的误差最小化到期望的输出Ydes,从而得到
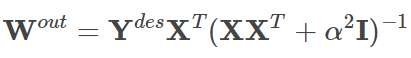
我们可以使用伪逆矩阵例程在最小二乘意义上求解上式,这些例程通常包含在各种计算机语言中,其中一些可以利用矩阵的稀疏性。非零值确保Wout的范数不会变大,这改善了系统对不同输入的普遍性并增加了噪声容限。我们还可以使用梯度下降方法的解决方案,这在矩阵维度很大时很有用,并利用来自深度学习社区的工具包利用图形处理单元。使用递归最小二乘法是另一种方法。
RC可以在预测任务中很好地工作。例如,当在训练之前将储层动力学投射到较低维度的相空间时,可以学习动力系统的吸引子[3]。我们还可以通过标准训练方法学习吸引子,并从RC产生的时间序列中准确地找到Lyapunov指数,甚至是时空动力系统[7]。此外,我们可以将预测的时间序列用作控制系统中的观察者[4],或者用于大型时空系统的数据同化而不使用基础模型[6]。这些结果表明RC是表征复杂动力系统的有力工具。虽然这些结论很有说服力,但为特定任务设计RC很大程度上是一种反复试验,而作者倾向于提供有效的结果,而不是那些失败的结果。以下是一个悬而未决的问题:我们如何优化模型中的参数以在预测或分类任务中获得最准确的预测,同时允许RC在类似于数据的数据上运行良好训练数据集?早期的研究集中在网络的所谓回声状态属性 - 输出最终应该忘记输入和一致性属性,相同试验的输出在某些时期应该是相似的。当Wres的光谱半径小于1时(对于bi = 0的情况),最初假设这些条件得到保证。
但是,这种情况忽略了输入动态(input dynamics),主要是X = 0稳定性的陈述。最近的工作开始解决单输入通道情况的这一缺点,证明在给定输入的情况下必须有一个完整的输出解决方案[5]。
虽然存在过去研究的基础,但许多需要定量和严格答案的问题仍然存在。例如,N必须有多大才能达到理想的错误率?我们应该如何调整γi相对于原始动力系统的时间尺度?为什么稀疏连接的储层经常表现最好?
在去年五月在犹他州Snowbird举行的2017年SIAM动力系统应用会议上,Edward Ott和作者组织了一次关于RCs的minisymposium讨论这些问题和其他问题。 Ott表明,RC可以学习动态系统的“气候”,并以可扩展的方式准确预测时空混乱。 Roger Brockett表示,密集的网络连接可能会导致储层节点的部分或完全同步,从而减少RC可以学习的波形的多样性。 Brian Hunt建议,当用于预测任务时,RC必须以广义的意义与输入数据同步。最后,我讨论了一种能够以超过几十MHz的速率进行预测的基于硬件的RC。
总之,RC可以作为一个能够学习其他系统动力学的通用动力系统。例如,当获得用于学习的动力系统的数据昂贵或困难时,这可能证明是有利的。虽然该领域正在迅速发展,但仍有大量空缺可供其他人加入。
References
[1] Jaeger, H., & Haas, H. (2004). Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science, 304(5667), 78-80.
[2] Larger, L., Baylón-Fuentes, A., Martinenghi, R., Udaltsov, V.S., Chembo, Y.K., & Jacquot, M. (2017). High-speed photonic reservoir computing using time-delay-based architecture: Million words per second classification. Phys. Rev. X, 7, 011015.
[3] Løkse, S., Bianchi, F.M., & Jessen, R. (2017). Training echo state networks with regularization through dimensionality reduction. Cogn. Comput., 9, 364.
[4] Lu, Z., Pathak, J., Hunt, B., Girvan, M., Brockett, R., & Ott, E. (2017). Reservoir observers: Model-free inference of unmeasured variables in chaotic systems. Chaos, 27, 041102.
[5] Manjunath, G., & Jaeger, H. (2013). Echo State Property Linked to an Input: Exploring a Fundamental Characteristic of Recurrent Neural Networks. Neur. Comp., 25, 671.
[6] Pathak, J., Hunt, B., Girvan, M., Lu, Z., & Ott, E. (2018). Model-free prediction of large spatiotemporally chaotic systems from data: A reservoir computing approach. Phys. Rev. Lett., 120, 024102.
[7] Pathak, J., Lu, Z., Hunt, B.R., Girvan, M., & Ott, E. (2017). Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Preprint, arXiv:1710.07313.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号