图卷积
原文：http://tkipf.github.io/graph-convolutional-networks/
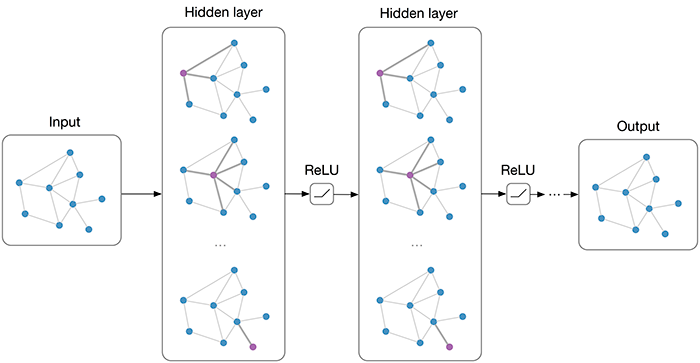
多层图卷积网络 (GCN) with first-order filters.
GCNs Part I: Definitions
给定一个网络结构G=(V,E),
1. N个节点，每个节点有D维信号或特征，即节点输入信号为N*D维矩阵， 记作X
2. 图结构表示，邻接矩阵A
3. 放入到图卷积网络中，得到输出Z，其中Z是N*F矩阵， F代表每个节点输出的特征维度
至于这个多层图卷积网络可以写成：
H(l+1)=f(H(l),A)
其中H(0)=X， H(L)=Z， 所以关键就是f(·,·)该怎么选取，以及内部参数的优化
GCNs Part II: A simple example
假设f(·,·)选取如下：
f(H(l),A)=σ(AH(l)W(l))
σ(⋅)为非线性函数（i.e., ReLU）.
需要注意的是:
1. 在和矩阵A相乘的时候，把邻居的信号进行了相加处理，但并没有加上自己的信号，所以我们需要强行加上自环.
2. 网络的规模，受到尺度影响，需要归一化操作. 最简单的就是使得归一化的A的行和为1，i.e., D−1A, 也就是对邻居信号做了平均. 但实际操作中，经常采用一个对称化的归一化操作，i.e., D−1/2AD−1/2
结合上面两条小trick，图卷积层可以表示为：
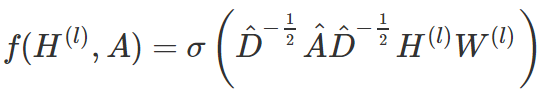
其中
，
为
节点度构成的对角矩阵
GCNs Part III: Embedding the karate club network
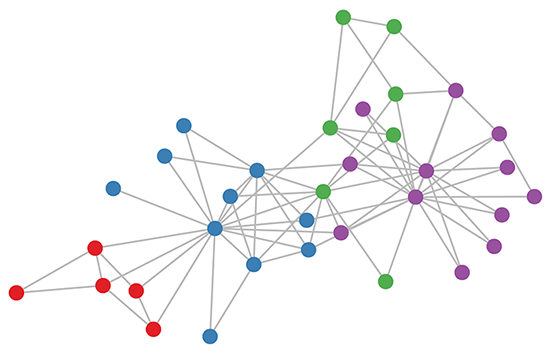
Karate club graph, colors denote communities obtained via modularity-based clustering (Brandes et al., 2008)
下面为如何用GCN来分析这个空手道俱乐部图（Karate club graph）
1. 采用3层GCN，随机初始化权重
2. 输入X=I, 因为我们这里没有节点特征.
然后我们就可以进行前向传播了，通过这3层传播，我们就可以得到每个节点对应的输出。如下图（此时，还没训练！）：
CN embedding (with random weights) for nodes in the karate club network.
PS: DeepWalk(Perozzi et al., KDD 2014) 能够非监督的学到相似的嵌入结果
