格兰杰因果 Granger causality
格兰杰因果关系(Granger causality )是基于预测的因果关系统计概念。根据格兰杰因果关系,如果信号X1“格兰杰Causes”(或“G-Causes”)信号X2,则X1的过去值应该包含有助于预测X2的信息,并且超过仅包含在X2的过去值中的信息。其数学公式基于随机过程的线性回归模型(Granger 1969)。当然也有对非线性情况的扩展,但是这些扩展在实践中通常更难以应用。
格兰杰因果关系(或“G因果关系”)于20世纪60年代发展起来,自那以来,已广泛应用于经济学。然而,仅仅在过去的几年里,神经科学的应用开始流行起来。
个人解释by Clive Granger
关于如何定义因果关系的话题让哲学家们忙了两千多年,但是现在都还没有得到解决。这是一个令人深思的问题,有许多种答案试图解释因果关系,但都并不能使所有人信服,它仍然具有一定的挑战性。研究者希望,如果他们认为已经找到了一个“原因”,这应该是一个深刻的基本关系,并且拥有potential。
在20世纪60年代早期,我(Clive Granger)正在考虑一对明显相互关联的随机过程,我想知道这种关系是否可以分解为一对单向关系。有人建议我看一下非常着名的数学家Norbert Weiner提出的因果关系的定义,所以我将这个定义(Wiener 1956)改编成实用的形式并进行了讨论。
应用经济学家发现这个定义便于理解和应用,并且它的具体应用开始出现。但是,有几位作者表示,“当然,这不是真正的因果关系,它只是格兰杰因果关系。”因此,从一开始,在实际应用中,使用Granger Causality这个术语来区别于其他定义。
基本的“Granger因果关系”定义非常简单。假设我们有三项Xt,Yt和Wt,并且我们首先尝试使用过去的Xt和Wt项来预测Xt+1。然后我们尝试使用过去的Xt,Yt和Wt来预测Xt+1。如果根据标准成本函数,发现第二个预测更成功,那么Y的过去似乎包含有助于预测Xt+1的信息,这些信息并不包含在过去的Xt或Wt。特别是,向量Wt可能是一个可解释的变量。因此,Yt会“格兰杰导致”Xt+1,如果(a)Yt出现在Xt+1之前; 并且(b)它包含能够预测Xt+1中有用的信息,这些信息在其他合适的变量中找不到。
当然,Wt越大,选择的内容就越仔细,Yt越严格。最终,Yt可能似乎包含有关Xt+1的独特信息,这在其他变量中找不到,这就是为什么“因果关系”标签可能是合适的。
这个定义很大程度上依赖于原因cause出现在效应effect之前,这是大多数因果关系定义的基础,但并不是全部。一些含义是Yt可能导致Xt+1,Xt导致Yt+1,相当于是一个反馈随机系统。但是,对于确定性过程(例如指数趋势)是不可能是casuse或者caused by另一个变量。
人们普遍认为,虽然它不能涵盖因果关系的所有方面,但足以在实际测试中得以应用。
Mathematical formulation
G-因果关系通常在线性回归模型的背景下进行测试。为了说明,考虑两个变量X1和X2的二元线性自回归模型:

其中p是包含在模型中的滞后观测值的最大数量(模型阶数),矩阵A包含模型的系数(即,每个滞后观测值对X1(t)和X2(t)的贡献,E1和E2是每个时间序列的残差(预测误差)。 在第一(或第二)方程中包含X2(或X1),如果E1(或E2)的方差降低了,则称X2(或X1) Granger-(G)-causes X1(或X2)。换句话说,如果A12中的系数与0显著不同,X2 G-引起X1。这可以通过F-test, 根据0假设A12 = 0,假设X1和X2协方差平稳,G因果互作用的大小可以用相应的F统计量的对数来估计(Geweke 1982)。 实际中要注意模型选择标准,如贝叶斯信息标准(BIC,(Schwartz 1978))或Akaike信息标准(AIC,(Akaike 1974))可以用来确定合适的模型阶数p。
正如上面所述,G因果关系可以很容易地扩展到n变量的情况,其中n> 2,估计一个n变量自回归模型。在这种情况下,如果X2的滞后观测值有助于预测X1时,并且同时也考虑到所有其他变量X3 ... XN的滞后观测值,那么X2 G-将导致X1。 (这里,'X3 ... XN对应于上一节中集合W中的变量; 另请参阅Boudjellaba et al。(1992)关于使用自回归移动平均(ARMA)模型的解释。)此多变量扩展版本,有时被称为'条件'G因果关系(Ding et al. 2006)是非常有用的,因为多个变量之间的重复配对分析有时会产生令人误解的结果。例如,重复的双变量分析将无法消除下图中两种连接模式的歧义。相比之下,条件/多变量分析将推断X到Y的因果关系,只要X中的过去信息有助于预测未来Y和超越beyond这些信号由Z为中介。另一个有价值的条件G因果关系例子: 单个信号源驱动两个具有不同时间延迟的输出。双变量分析,但不是多变量分析,会错误地推断出从较短延迟输出到较长延迟输出的因果联系。
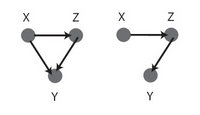
Two possible connectivities that cannot be distinguished by pairwise analysis. Adapted from Ding et al. (2006).
上述G因果公式的应用对数据做出了两个重要假设:(i)它是协方差平稳的(即每个时间序列的均值和方差不随时间变化);(ii)它可以可以通过线性模型进行充分描述。
Spectral G-causality
通过傅里叶方法,可以检查谱Spectral域中的G因果关系(Geweke,1982; Kaminski等,2001)。这对于神经生理学信号非常有用,其中频率分解通常是比较有意思的。直观地说,从X1到X2的频谱G因果关系度量了在频率f处,X2贡献给X1的分数。
为了完整性,我们在下面给出了谱G因果关系的数学细节。 通过傅里叶变换可以得到,

矩阵A的元素为,
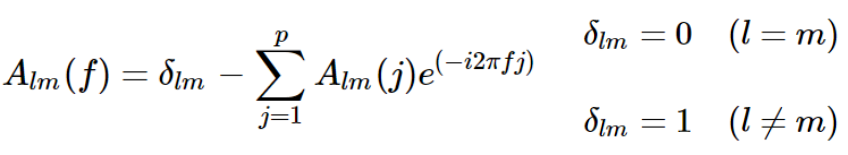
重新写原来的方程,
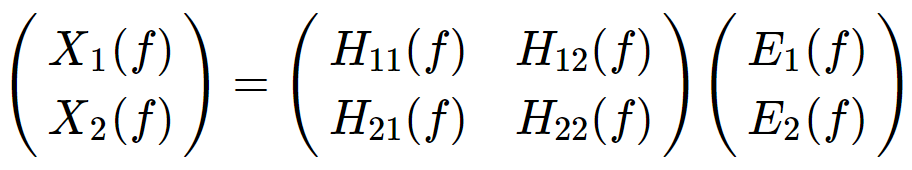
其中,
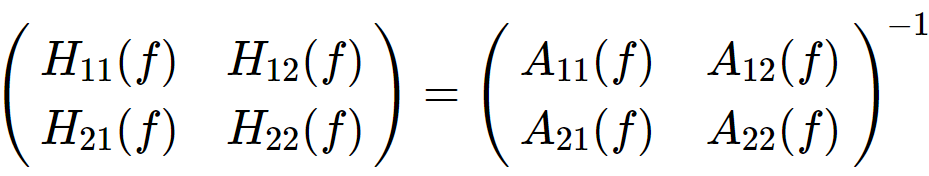
H称作为传递矩阵(transfer matrix),现在可以得到普矩阵S,

*代表矩阵的共轭转置,Σ 是残差E(t)的协方差矩阵。 从节点j到i的谱G-causality为,
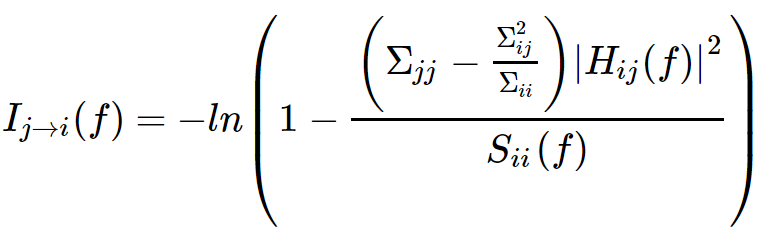
其中Sii(f)是变量i在频率为f处的功率谱。 (该分析改编自(Brovelli等2004; Kaminski等2001))
Chen et al (2006)的工作指出,将Geweke提出的谱G因果关系应用于多变量(> 2)神经生理学时间序列有时会导致在某些频率处的负因果关系,这是一个有点违背(evade)物理解释的结果。他们提出了修改后的Geweke度量的条件版本,它可以通过使用分块矩阵( partition matrix)方法来克服这个问题。 Breitung和Candelon(2006)和Hosoya(1991)讨论了谱G因果关系的其他版本。
与谱G因果关系密切相关的两种方法是partial directed coherence(Baccala&Sameshima,2001)和 directed transfer function定向传递函数(Kaminski et al。2001;注意这些作者表明了定向传递函数和谱G-因果关系之间的等价性)。对于这些方法之间的比较结果,参见Baccala和Sameshima(2001),Gourevitch等人(2006)和Pereda等人(2005年)。与G因果关系的原始时域公式不同,这些频谱测量的统计特性尚未完全阐明。这意味着显着性检验通常依赖于替代(surrogate)数据,并且信号预处理(例如,平滑,过滤)对测量因果关系的影响仍不清楚。
Limitations and extensions
Linearity
G因果关系的原始公式只能给出有关信号线性特征的信息。现在已经存在对非线性情况的扩展,但是这些扩展在实践中可能更难以使用,并且他们的统计特性不太清楚。在Freiwald等人的方法中。 (1999)将全球非线性数据分为局部线性邻域(参见Chen et al.2004),而Ancona et al。 (2004)使用径向基函数方法来执行全局非线性回归。
Stationarity
G-因果关系的应用假定分析信号是协方差平稳的。假设非平稳信号的足够短的窗口局部平稳,可以通过使用窗口技术(Hesse et al.2003)来处理非平稳数据。一个相关的方法利用了许多神经生理学实验的试验性质(Ding等,2000)。在这种方法中,来自不同试验的时间序列被视为具有局部平稳段的非平稳随机过程的单独实现。
Dependence on observed variables
关于G因果关系的所有实现的一般评论是,它们完全依赖于适当的变量选择。显然,没有纳入回归模型的因果因素不能用来表示输出。因此,G-因果关系不应被解释为直接反映物理因果链。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号