Wasserstein Generative Adversarial Nets (WGAN ) and CGAN

GAN目前是机器学习中非常受欢迎的研究方向。主要包括有两种类型的研究，一种是将GAN用于有趣的问题，另一种是试图增加GAN的模型稳定性。

事实上，稳定性在GAN训练中是非常重要的。起初的GAN模型在训练中存在一些问题，e.g., 模式塌陷（生成器演化成非常窄的分布，只覆盖数据分布中的单一模式）。模式塌陷的含义是发生器只能产生非常相似的样本（例如MNIST中的单个数字），即所产生的样本不是多样的。这当然违反了GAN的初衷。

GAN中的另一个问题是没有指很好的指标或度量说明模型的收敛性。生成器和鉴别器的损失并没有告诉我们关于这方面的任何信息。当然，我们可以通过查看生成器产生的数据来监控训练过程。但是，这是一个愚蠢的手动过程。所以，我们需要一个可解释的指标告诉我们训练过程的好坏。

Wasserstein GAN

Wasserstein GAN（WGAN）是一种新提出的GAN算法，可以在一定程度解决上述两个问题。对于WGAN背后的直觉和理论背景，可以查看相关资料。

整个算法的伪代码如下：

我们可以看到该算法与原始GAN算法非常相似。 但是，对于WGAN，我们根据上面的代码需要注意到下几点：

1. 损失函数中没有log。判别器D(X)的输出不再是一个概率（标量），同时也就意味着没有sigmoid激活函数
2. 对于判别器D(X)的权重W进行裁剪
3. 训练判别器的次数多于生成器
4. 采用RMSProp优化器，代替原先的ADAM优化器
5. 非常低的learning rate, $\mathrm{\alpha =0.00005}$

WGAN TensorFlow implementation

GAN的基本实现可以在上一篇文章中介绍过。 我们只需要稍微修改下传统的GAN。 首先，让我们更新我们的判别器D(X)

""" Vanilla GAN """
def discriminator(x):
    D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1)
    out = tf.matmul(D_h1, D_W2) + D_b2
    return tf.nn.sigmoid(out)

""" WGAN """
def discriminator(x):
    D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1)
    out = tf.matmul(D_h1, D_W2) + D_b2
    return out

接下来，修改loss函数，去掉log：

""" Vanilla GAN """
D_loss = -tf.reduce_mean(tf.log(D_real) + tf.log(1. - D_fake))
G_loss = -tf.reduce_mean(tf.log(D_fake))

""" WGAN """
D_loss = tf.reduce_mean(D_real) - tf.reduce_mean(D_fake)
G_loss = -tf.reduce_mean(D_fake)

在每次梯度下降更新后，裁剪判别器D(X)的权重：

# theta_D is list of D's params
clip_D = [p.assign(tf.clip_by_value(p, -0.01, 0.01)) for p in theta_D]

然后，只需要训练更多次的判别器D(X)就行了

D_solver = (tf.train.RMSPropOptimizer(learning_rate=5e-5)
            .minimize(-D_loss, var_list=theta_D))
G_solver = (tf.train.RMSPropOptimizer(learning_rate=5e-5)
            .minimize(G_loss, var_list=theta_G))

for it in range(1000000):
    for _ in range(5):
        X_mb, _ = mnist.train.next_batch(mb_size)

        _, D_loss_curr, _ = sess.run([D_solver, D_loss, clip_D], feed_dict={X: X_mb, z: sample_z(mb_size, z_dim)})

    _, G_loss_curr = sess.run([G_solver, G_loss], feed_dict={z: sample_z(mb_size, z_dim)})

 

Conditional GAN

这里顺便简短的介绍下CGAN。

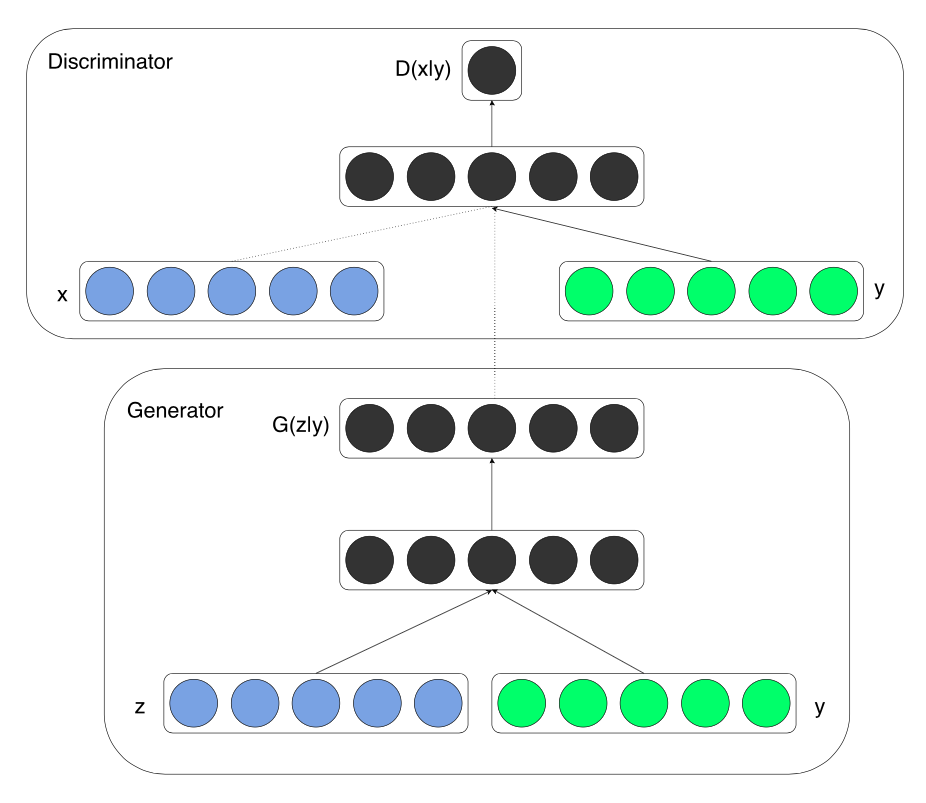
只需要在判别器D(X)和生成器G(Z)中的输入层额外拼接上向量y就可以了

额外的输入y：

y = tf.placeholder(tf.float32, shape=[None, y_dim])

再将它加入到判别器D(X)和生成器G(Z)中：

def generator(z, y):
    # Concatenate z and y
    inputs = tf.concat(concat_dim=1, values=[z, y])

    G_h1 = tf.nn.relu(tf.matmul(inputs, G_W1) + G_b1)
    G_log_prob = tf.matmul(G_h1, G_W2) + G_b2
    G_prob = tf.nn.sigmoid(G_log_prob)

    return G_prob


def discriminator(x, y):
    # Concatenate x and y
    inputs = tf.concat(concat_dim=1, values=[x, y])

    D_h1 = tf.nn.relu(tf.matmul(inputs, D_W1) + D_b1)
    D_logit = tf.matmul(D_h1, D_W2) + D_b2
    D_prob = tf.nn.sigmoid(D_logit)

    return D_prob, D_logit

改变权重的维数：

# Modify input to hidden weights for discriminator
D_W1 = tf.Variable(shape=[X_dim + y_dim, h_dim]))

# Modify input to hidden weights for generator
G_W1 = tf.Variable(shape=[Z_dim + y_dim, h_dim]))

构建新的网络：

# Add additional parameter y into all networks
G_sample = generator(Z, y)
D_real, D_logit_real = discriminator(X, y)
D_fake, D_logit_fake = discriminator(G_sample, y)

训练时，额外加入y即可：

X_mb, y_mb = mnist.train.next_batch(mb_size)

Z_sample = sample_Z(mb_size, Z_dim)
_, D_loss_curr = sess.run([D_solver, D_loss], feed_dict={X: X_mb, Z: Z_sample, y:y_mb})
_, G_loss_curr = sess.run([G_solver, G_loss], feed_dict={Z: Z_sample, y:y_mb})

 

接下来进行生成器验证的时候，可以固定y的值：

n_sample = 16
Z_sample = sample_Z(n_sample, Z_dim)

# Create conditional one-hot vector, with index 5 = 1
y_sample = np.zeros(shape=[n_sample, y_dim])
y_sample[:, 7] = 1

samples = sess.run(G_sample, feed_dict={Z: Z_sample, y:y_sample})

 

 PS:用下面的loss函数，收敛特别快，效果会更加好。

D_loss_real=tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_real,labels=tf.ones_like(D_real)))
D_loss_fake=tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake,labels=tf.zeros_like(D_fake)))
D_loss=D_loss_real+D_loss_fake
G_loss=tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake,labels=tf.ones_like(D_fake)))