连接

常系数线性差分方程的求解

地址： 

1. https://wenku.baidu.com/view/f191d2ea102de2bd960588ae.html  

2. https://www.zhihu.com/question/25217301

3. https://wenku.baidu.com/view/9716c9f9770bf78a65295431.html

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

( 这里用F_n 代表斐波那契数列第 n 项，且约定 F_0=0 )

设有一个矩阵 M 使得\begin{pmatrix}F_n\\F_{n+1}\end{pmatrix}=M\begin{pmatrix}F_{n-1}\\F_{n}\end{pmatrix}

设 M=\begin{pmatrix}A&C\\B&D\end{pmatrix} 就有\begin{pmatrix}F_n\\F_{n+1}\end{pmatrix}=\begin{pmatrix}AF_{n-1}+CF_{n}\\BF_{n-1}+DF_{n}\end{pmatrix}

直接令 A=0 ，再令 C=B=D=1 ，得到 M=\begin{pmatrix}0&1\\1&1\end{pmatrix}

把 M 特征分解，就可以求出 \begin{pmatrix}F_n\\F_{n+1}\end{pmatrix} 的通项式

\begin{pmatrix}F_n\\F_{n+1}\end{pmatrix}=M\begin{pmatrix}F_{n-1}\\F_{n}\end{pmatrix}\Rightarrow\begin{pmatrix}F_n\\F_{n+1}\end{pmatrix}=M^n\begin{pmatrix}F_{0}\\F_{1}\end{pmatrix}\Rightarrow\begin{pmatrix}F_n\\F_{n+1}\end{pmatrix}=PD^nP^{-1}\begin{pmatrix}0\\1\end{pmatrix}

解特征方程 \det(M-\lambda I)=0 得到M的特征值\lambda=\frac{1\pm\displaystyle\sqrt{5}}{2}

然后得到两个的特征向量 \begin{pmatrix}1\\\\\displaystyle\frac{1\pm\sqrt 5}{2}\end{pmatrix}

\begin{aligned}P^{-1}&=\begin{vmatrix}1&1\\\\\displaystyle\frac{1+\sqrt 5}{2}&\displaystyle\frac{1-\sqrt 5}{2}\end{vmatrix}^{-1}\begin{pmatrix}\displaystyle\frac{1-\sqrt 5}{2}&-\displaystyle\frac{1+\sqrt 5}{2}\\\\-1&1\end{pmatrix}^{\rm T}\\&=\begin{pmatrix}\displaystyle\frac{\sqrt 5-1}{2\sqrt 5}&\displaystyle\frac{1}{\sqrt 5}\\\\\displaystyle\frac{\sqrt 5 + 1}{2\sqrt 5}&\displaystyle-\frac{1}{\sqrt 5}\end{pmatrix}\end{aligned}

\begin{aligned}F_n&=\begin{pmatrix}1&0\end{pmatrix}\begin{pmatrix}1&1\\\\\displaystyle\frac{1+\sqrt 5}{2}&\displaystyle\frac{1-\sqrt 5}{2}\end{pmatrix}\begin{pmatrix}\displaystyle\left(\frac{1+\sqrt 5}{2}\right)^{n}&0\\0&\displaystyle\left(\frac{1-\sqrt 5}{2}\right)^n\end{pmatrix}\begin{pmatrix}\displaystyle\frac{\sqrt 5-1}{2\sqrt 5}&\displaystyle\frac{1}{\sqrt 5}\\\\\displaystyle\frac{\sqrt 5 + 1}{2\sqrt 5}&\displaystyle-\frac{1}{\sqrt 5}\end{pmatrix}\begin{pmatrix}0\\1\end{pmatrix}\\&=\begin{pmatrix}1&0\end{pmatrix}\begin{pmatrix}1&1\\\\\displaystyle\frac{1+\sqrt 5}{2}&\displaystyle\frac{1-\sqrt 5}{2}\end{pmatrix}\begin{pmatrix}\displaystyle\left(\frac{1+\sqrt 5}{2}\right)^{n}&0\\0&\displaystyle\left(\frac{1-\sqrt 5}{2}\right)^n\end{pmatrix}\begin{pmatrix}\displaystyle\frac{1}{\sqrt{5}}\\\\\displaystyle-\frac{1}{\sqrt{5}}\end{pmatrix}\\&=\frac{2^{-n}}{\sqrt 5}\begin{pmatrix}1&0\end{pmatrix}\begin{pmatrix}1&1\\\\\displaystyle\frac{1+\sqrt 5}{2}&\displaystyle\frac{1-\sqrt 5}{2}\end{pmatrix}\begin{pmatrix}\displaystyle\left(1+\sqrt 5\right)^n\\-\displaystyle\left(1-\sqrt 5\right)^n\end{pmatrix}\\&=\frac{\displaystyle\left(\frac{1+\displaystyle\sqrt{5}}{2}\right)^n-\displaystyle\left(\frac{1-\displaystyle\sqrt{5}}{2}\right)^n}{\displaystyle\sqrt{5}}\end{aligned}

所以

F_n=\frac{\displaystyle\left(\frac{1+\displaystyle\sqrt{5}}{2}\right)^n-\displaystyle\left(\frac{1-\displaystyle\sqrt{5}}{2}\right)^n}{\displaystyle\sqrt{5}}

 

相同的方法可以求形如 A_{n}=c_1A_{n-1}+c_2A_{n-2} 递推式的通项公式，

只要让 M=\begin{pmatrix}0&1\\c_2&c_1\end{pmatrix} ，剩下的步骤一模一样

甚至还可以扩展到更高维度的矩阵求形如 A_{n}=c_1A_{n-1}+c_2A_{n-2}+\cdots+c_mA_{n-m} 的通项公式

当然，前提是 M 非奇异，且拥有 m个线性无关的特征向量

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

解差分方程
x(n+2)=x(n+1)+x(n)
Z^{2} X(Z)=Z X(Z)+X(Z)
X(Z)=\frac{1}{Z^{2}-Z-1} =\frac{1}{(Z-\frac{1+\sqrt{5} }{2} )(Z-\frac{1-\sqrt{5} }{2} )} =\frac{1}{\sqrt{5}} (\frac{Z}{Z-\frac{1+\sqrt{5} }{2}} -\frac{Z}{Z-\frac{1-\sqrt{5} }{2}} )
求逆Z变换
x\left( n \right) =\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5} }{2} )^{n}-\frac{1-\sqrt{5} }{2} )^{n}]

 

 -----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

 

作者：唐小谦
链接：https://www.zhihu.com/question/25217301/answer/158753864
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

感谢大家的点赞和评论！在这里统一向各位说声抱歉，我把这个解答称为初等方法确实不够严谨，看似初等的方法里面实际上隐藏了并不初等的概念。确切地说，如果要正确理解下面这个等式

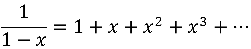
需要一些形式幂级数环的简单知识（包括环的概念，环中可逆元的概念）。

因为考虑的是形式幂级数，在向形式变元x代入具体的数之前并不牵涉收敛性问题，也无需使用泰勒展开等工具。因此，我仍然认为这是一个中学生可以接受的解答，再加上生成函数非常有价值，应该介绍给大家。

至于“初等”与“高等”之争，我认为是一件好事，因为大家所熟知的初等数学里，也有很多事情需要借助高等数学的知识才能说清楚，而我们国家的中学数学教材与大学数学教材其实脱节很严重。但状况并不应该如此，中学数学里的内容有一些非常有趣而深刻的背景可以挖掘出来，而不是只教大家做题。最近在对这方面的内容做一个梳理和总结，系列文章

奇葩数学史 - 知乎专栏 新鲜上线，希望大家多提意见！

以下是原答。

－－－－－－－－－－－－－－－－－－分割线－－－－－－－－－－－－－－－－－－－

纯手工初等方法。记斐波那契数列第n项为F_n，则F_n=F_{n-2}+F_{n-1}。

构造一个与\{F_n\}有关的幂级数

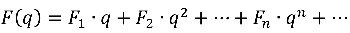
这个函数被称为斐波那契数列的生成函数，因为它的幂级数展开完全决定了 \{F_n\}，展开式中q^n的系数就是斐波那契数列的第n项。

对于一般数列的生成函数，我们暂且按下不表，先来看看有没有办法求这个特殊的F。我们没有别的选择，唯一的条件是F_n=F_{n-1}+F_{n-2}，这个等式应该能够诱导出一个F满足的方程。

确实如此，F_n是q^n的系数，F_{n-1}和F_{n-2}则分别是q^{n-1}和q^{n-2}的系数，要想让它们匹配在一起，就要想办法让它们对应同一个q^n。这其实很容易办到，q\cdot F中q^n的系数就是F_{n-1}，同理， q^2\cdot F中q^n的系数就是F_{n-2}。

于是，F-q\cdot F-q^2\cdot F中q的所有高于1的幂次前的系数都变成了0，只剩下了q。从而

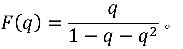
如果你能把 \frac{q}{1-q-q^2} 展开成幂级数的形式，就自然求出了斐波那契数列的通项。

现在，让我们回忆一个中学里十分常用的技巧

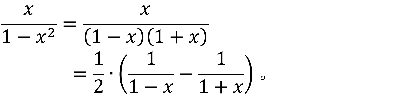
这件事情的本质是将分母中的多项式作因式分解，将分母含有二次项的分式转换成分母只含一次项，而分母只含一次项的分式很容易写成幂级数

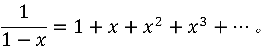
回到F=\frac{q}{1-q-q^2} ，我们可以用待定系数法完成上面的过程，设

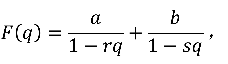
于是

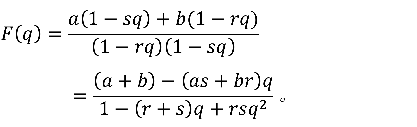
我们得到一个四元方程组

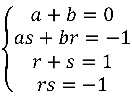
这个方程组的难度只能称为小喽喽级别，凭借后两个方程解出

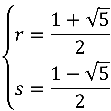
代入到前两个方程中即得 a=\frac{1}{\sqrt{5}} ，b=-\frac{1}{\sqrt{5}} 。

所以

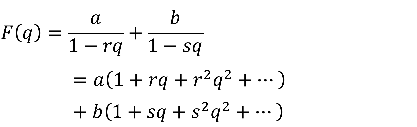
蕴含了斐波那契数列的通项为

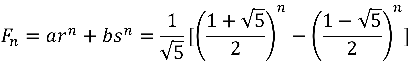
看起来不太像整数，但确实如此。

生成函数是处理数列的常用工具，是离散走向连续的桥梁，很多人们关心的离散信息都复刻在这样一条DNA上。你们一定很奇怪我在定义F时用的自变量是q而不是x，事实上我想通过这种方式提醒大家无穷展开的广泛性，当q被某种具有周期性的基本函数替代时，我们就得到了傅立叶展开。作为著名的费马大定理证明核心的谷山－志村－韦伊猜想说的就是某种刻画了椭圆曲线模p点个数信息的生成函数可以与模形式的傅立叶展开对应起来，有机会再跟大家详聊。

以上。

 

posted @ 2017-09-21 11:16  朱群喜_QQ囍_海疯习习  阅读(1588)  评论(0)  编辑  收藏  举报
Map