Andronov-Hopf bifurcation

地址：http://www.scholarpedia.org/article/Andronov-Hopf_bifurcation

 

Andronov-Hopf bifurcation is the birth of a limit cycle from an equilibrium in dynamical systems generated by ODEs, when the equilibrium changes stability via a pair of purely imaginary eigenvalues. The bifurcation can be supercritical or subcritical, resulting in stable or unstable (within an invariant two-dimensional manifold) limit cycle, respectively.

Definition

Consider an autonomous system of ordinary differential equations (ODEs)

　　　　

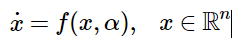
depending on a parameter α∈R , where f is smooth.

• Suppose that for all sufficiently small |α| the system has a family of equilibria x₀(α) .
• Further assume that its Jacobian matrix A(α)=fx(x0(α),α) has one pair of complex eigenvalues

λ_1,2(α)=μ(α)±iω(α)

that becomes purely imaginary when α=0 , i.e., μ(0)=0 and ω(0)=ω₀>0 . Then, generically, as α passes through α=0 , the equilibrium changes stability and a unique limit cycle bifurcates from it. This bifurcation is characterized by a single bifurcation condition Re λ_1,2=0 (has codimension one) and appears generically in one-parameter families of smooth ODEs.