最小可观(Minimal Observability Problem in Conjunctive Boolean Networks)
1. 什么是 conjunctive Boolean network (CBN)
仅仅包含and运算。
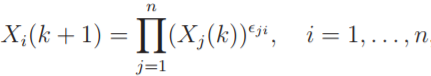
下面这个式子为恒定更新函数
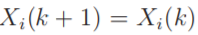
2. 什么是可观
定义在时刻k是CBN的状态为 X(k) := [X1(k) . . . Xn(k) ]′ 以及输出为Y(k) :=[Y1(k) . . . Ym(k) ]′ .
a). CBN在离散时间{0, 1, . . . , N}上可观,如果对于任意两个不同的初始状态X(0)和X'(0)产生不同的输出{Y(0),...,Y(N)}和{Y’(0),...,Y’(N)}。
b). CBN可观,如果存在N,使得a)成立。
3. 可观必须具有的性质(等价条件)
a) 性质O1:对于每一个非直接可观的节点Xi,Xi是某一个节点Xj唯一的入边的节点,即,存在一个节点Xj,使得,Nin(Xj)=Xi。
b) 性质O2:对于每一个仅由非直接可观的节点组成的环C。C包含一个节点Xi,Xi是某一个节点Xj唯一的入边的节点,即,存在一个节点Xj,使得,Nin(Xj)=Xi并且Xj在环C的外部。
4. 例子
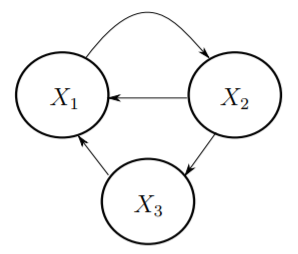
Ex 1. 添加观测器,Y1(k)=X1(K)。则给定输出Y1(0),Y1(1),就可以推出初始状态分别为X1(0)=Y1(0),X2(0)=Y1(1)。
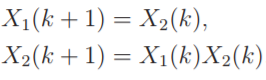
Ex 2. CBN不具有性质O1,非可观节点X3,不存在任何一个节点,使得性质O1成立。[0 0 0]'和[0 0 1]'是无法区分的,因为它们的输出Y1(k)=0对于所有的k≥0。
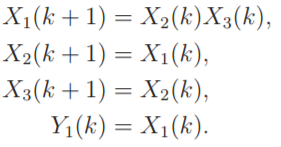
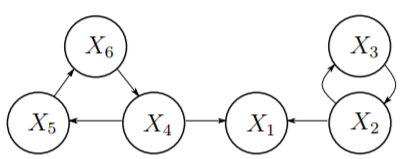
Ex 3. CBN满足性质O1,但是不满足性质O2。对于由X4,X5,X6构成的环,X4不是X1唯一的进入的节点。[0 0 0 0 0 0]‘和[0 0 0 1 1 1]'对应的输出Y1(k)=0对于所有的k≥0。
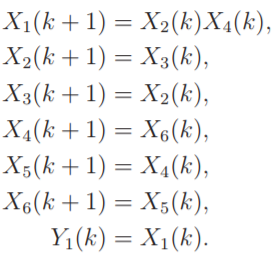




 浙公网安备 33010602011771号
浙公网安备 33010602011771号