Flow-based model

文章1:  NICE: NON-LINEAR INDEPENDENT COMPONENTS ESTIMATION

文章2：Real-valued Non-Volume Preserving （RealNVP）

文章3：Glow: Generative Flow with Invertible 1x1 Convolutions

NICE

学习目标：找一个变换h=f(x)，使得变换后的分布的每个分量是独立的

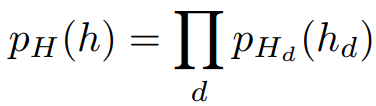
 我们假设h和x的维度是一样的，f是可逆的，则我们有

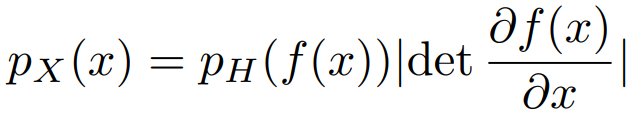
 并且，我们希望f的Jacobian矩阵和f⁻¹比较容易计算。如果这是可以操作的，那么我们可以直接采样p_X(x),

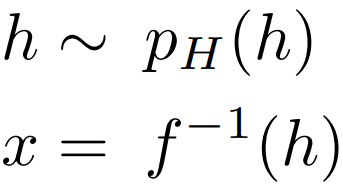
 这个f的设计的主要核心思想是，将x分裂成两部分(x1,x2),然后变换成(y1,y2),

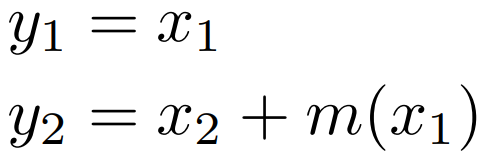
m可以是任意的函数(i.e., a ReLU MLP). 注意到，Jacobian矩阵的行列式是单位阵，并且非常容易算逆函数，

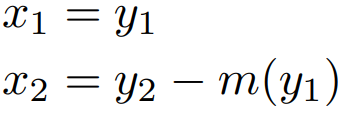
当然我们可以定义更一般性的架构,，加性交错coupling的架构。并且可以有一层一层的变换，有种flow的感觉。

 

 

 我们可以定义最大似然函数：

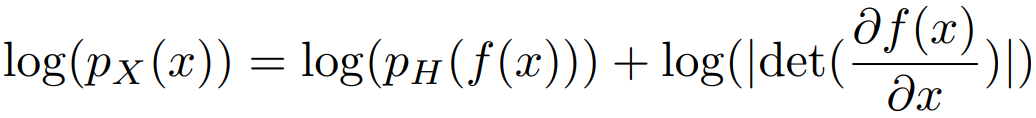
p_H(h)：先验分布，可以事先定义好的，比如各向同性的高斯分布.如果h的每个分量都是独立的，我们可以写成，

 

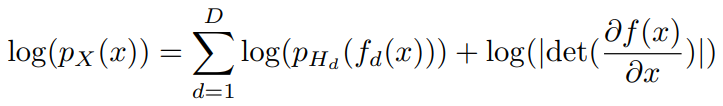
RealNVP 

分裂的办法：

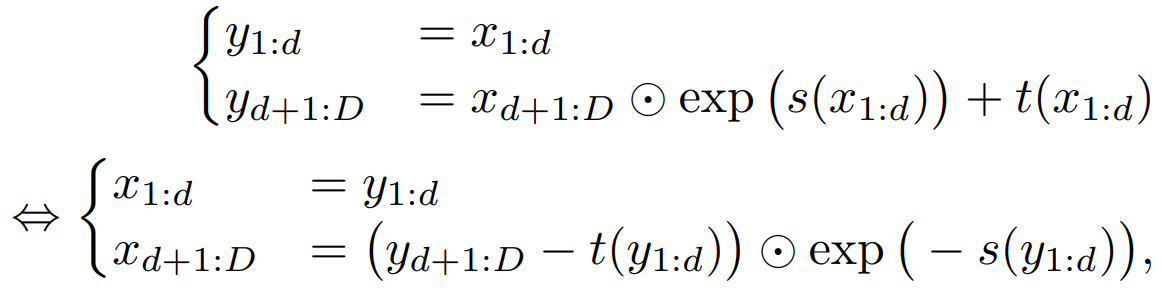
s 和 t 是 scale 和 translation, 函数，R^d ——>R^D−d, 

对应的Jacobia矩阵，

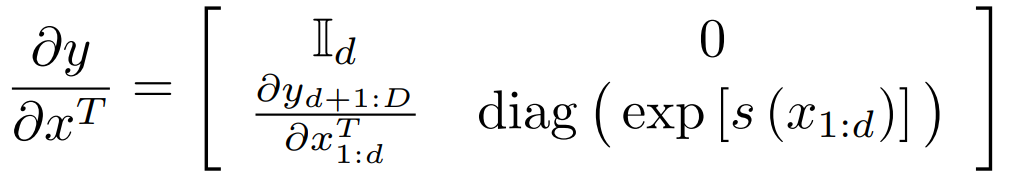
PS: 由于我们算逆函数和Jacobia矩阵的过程中，都没有涉及到s和t的逆函数，所以s和t是可以任意复杂的，i.e.，神经网络。

 

Glow

核心引入了1x1可逆卷积操作: C个1*1的卷积核，即对每个（共W*H个）粉色棍子，用C个橙色的棍子，变成红色的棍子（图中只显示了红色棍子的其中一个方块）。 为了保证卷积核A的可逆性，需要加一些约束， i.e., 将−log|det A|加入到loss中.

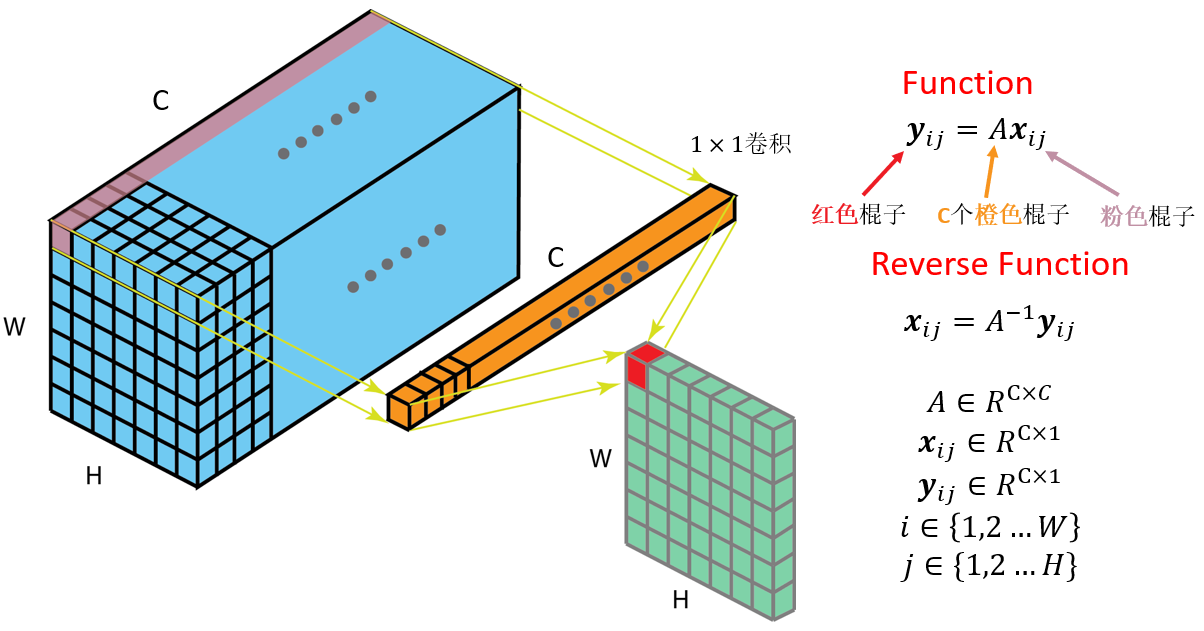
 1*1可逆卷积

 三种不同方案的loss曲线比较