引言
我们知道,对数函数 ln(x) 可以展开为泰勒级数:
 |
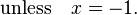 |
但是下面这个泰勒级数展开式收敛得更快:
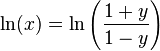 |
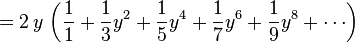 |
经过简单计算可知上式中 y = (x - 1) / (x + 1) 。
实现该算法的 C# 程序
根据上面的第二个泰勒级数展开式,我们可以为 C# 的 decimal 数据类型实现如下的 Log 扩展方法:
1 using System; 2 3 namespace Skyiv.Extensions 4 { 5 static class DecimalExtensions 6 { 7 static readonly decimal ln10 = 2.3025850929940456840179914547m; 8 static readonly decimal lnr = 0.2002433314278771112016301167m; 9 10 public static decimal Log10(this decimal x) 11 { 12 return Log(x) / ln10; 13 } 14 15 public static decimal Log(this decimal x) 16 { 17 if (x <= 0) throw new ArgumentException("Must be positive"); 18 int k = 0, l = 0; 19 for (; x > 1; k++) x /= 10; 20 for (; x <= 0.1m; k--) x *= 10; // ( 0.1, 1 ] 21 for (; x < 0.9047m; l--) x *= 1.2217m; // [ 0.9047, 1.10527199 ) 22 return k * ln10 + l * lnr + Logarithm((x - 1) / (x + 1)); 23 } 24 25 static decimal Logarithm(decimal y) 26 { // y in ( -0.05-, 0.05+ ), return ln((1+y)/(1-y)) 27 decimal v = 1, y2 = y * y, t = y2, z = t / 3; 28 for (var i = 3; z != 0; z = (t *= y2) / (i += 2)) v += z; 29 return v * y * 2; 30 } 31 } 32 }
在这个程序中:
- 第 7 行是事先计算出来的 ln(10) 的值,用于第 12 行和第 22 行。
- 第 8 行是事先计算出来的 ln(1.2217) 的值,用于第 22 行。
- 第 15 至 23 行的 Log 扩展方法就是用来计算自然对数了。
- 通过第 19 至 20 行,将参数 x 的值变换到 ( 0.1, 1 ] 的区间中。这两个循环只会执行其中的一个,且循环次数不超过 28 次。
- 通过第 21 行,进一步将参数 x 的值变换到 [ 0.9047, 1.10527199 ) 的区间中。这个循环执行次数不超过 11 次。
- 第 22 行通过调用 Logarithm 方法来计算自然对数。传入的参数是 (x - 1) / (x + 1),其范围大约在 ( -0.05, 0.05 ) 的区间中。
- 第 22 行的表达式是基于 ln(xy) = ln(x) + ln(y) 和 ln(xn) = n ln(x) 这两条对数函数的运算规则。当然,后者是前者的特例。
- 第 25 至 30 行的 Logarithm 方法使用泰勒级数来计算自然对数,它的参数 y 越接近零收敛得越快。
- 注意,它的返回值是 ln((1+y)/(1-y)),而不是 ln(y)。
- 这个算法还是很快的,第 28 行的 for 循环执行次数不会超过 10 次。
程序中相关常数的由来
上面程序中的 1.2217 和 0.9047 等常数是如何得到的呢?请看下面的计算:
work$ bc -l
bc 1.06
Copyright 1991-1994, 1997, 1998, 2000 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'.
scale=30
define x(y) { return (1+y)/(1-y); }
x(-0.05)
.904761904761904761904761904761
x(0.05)
1.105263157894736842105263157894
1.10526/0.9047
1.221686746987951807228915662650
l(1.2217)
.200243331427877111201630116698
l(1.2216)
.200161474922285626409839638619
quit
work$
上面使用 Linux 中的 bc 进行计算,l 代表 ln 函数,请参阅参数资料[3]。分析如下:
- 我们的目标是要将第 25 行的 Logarithm 方法的参数 y 控制在 ( -0.05, 0.05 ) 区间范围内。
- 由前面引言中知道,x = (1+y) / (1-y)。所以计算出 x 大约在 ( 0.9047, 1.10526 ) 区间范围内。
- 为了第 21 行的将 x 值变换到上述区间,计算出变换因子 1.10526 / 0.9047 ≈ 1.2217 。
- 这就得到第 8 行的 ln(1.2217) 的值。注意该值最后几位是 ...6698,舍入到 ...6700,误差相当小。(decimal 要求舍入到 28 个有效数字)
- 我原来在第 2 步采用区间 ( -0.90476, 1.105263 ),计算出来的变换因子是 1.105263 / 0.90476 ≈ 1.2216 。
- 相应的 ln(1.2216) 的最后几位是 ...8619,舍入到 ...8600,误差就稍微大了一点。
验证常数的值
让我们来验证一下前面计算的常数的值是否正确:
work$ bc -l
bc 1.06
Copyright 1991-1994, 1997, 1998, 2000 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'.
scale=30
r=1.2217
a=0.9047
b=a*r
b
1.10527199
define y(x) { return (x-1)/(x+1); }
y(a)
-.050034126109098545702735338898
y(b)
.050003985470779953710399196447
quit
work$
说明如下:
- 我们得到 x 在 [ 0.9047, 1.10527199 ) 区间范围内。
- 由前面的引言可知,y = (x - 1) / (x + 1),大约在 ( -0.05, 0.05 ) 区间范围内。
- 这说明我们以前的计算是正确的。
测试程序
下面是调用 decimal 数据类型的 Log 和 Log10 扩展方法的测试程序:
1 using System; 2 using Skyiv.Extensions; 3 4 class Tester 5 { 6 static void Main() 7 { 8 foreach (var x in new decimal[] { 4 / decimal.MaxValue, 9 0.0000001m, 0.0001m, 0.1m, 1, 1.2217m, 2, 10, 10000, 10 100000000, decimal.MaxValue }) 11 { 12 Console.WriteLine("x : " + x); 13 Console.WriteLine("ln: " + x.Log()); 14 Console.WriteLine("lg: " + x.Log10()); 15 Console.WriteLine(); 16 } 17 } 18 }
运行结果如下所示:
work$ dmcs Tester.cs DecimalExtensions.cs work$ mono Tester.exe x : 0.0000000000000000000000000001 ln: -64.472382603833279152503760732 lg: -28.000000000000000000000000000 x : 0.0000001 ln: -16.118095650958319788125940183 lg: -7.0000000000000000000000000000 x : 0.0001 ln: -9.210340371976182736071965819 lg: -4.0000000000000000000000000001 x : 0.1 ln: -2.3025850929940456840179914547 lg: -1 x : 1 ln: 0 lg: 0 x : 1.2217 ln: 0.2002433314278771112016301167 lg: 0.0869645738770510340282719812 x : 2 ln: 0.6931471805599453094172321215 lg: 0.3010299956639811952137388947 x : 10 ln: 2.3025850929940456840179914547 lg: 1 x : 10000 ln: 9.210340371976182736071965819 lg: 4.0000000000000000000000000001 x : 100000000 ln: 18.420680743952365472143931638 lg: 8.000000000000000000000000000 x : 79228162514264337593543950335 ln: 66.542129333754749704054283660 lg: 28.898879583742194740518933893
从上面运行结果可以看出,精度基本上达到了 28 位有效数字,比我前几天的“计算自然对数的快速算法”一文介绍的算法要好。







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· 展开说说关于C#中ORM框架的用法!
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?